
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчёт на прочность при изгибе. Понятие о расчётном и нормативном коэффициенте запаса.
|
|
По принципу независимости действия сил нормальное напряжение в произвольной точке, принадлежащей поперечному сечению бруса и имеющей координаты x, y, опр-ся суммой напр-й, обусловленных моментами Mx и My, т.е. 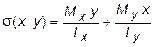 (5.26)
(5.26)
Mx = M× sina; My = M× cosa, где a - угол между плоскостью главного мемента М и осью Ох или Оу. (5.25)
Правило знаков для моментов: момент считается положительным, если в первой четверти координатной плоскости (там, где координаты x и y обе положительны) он вызывает сжимающие напряжения.
Если изгиб чистый, то один из моментов Mx или My равен 0 и выражение (5.26) принимает вид
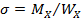 , где
, где 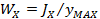 - осевой момент сопротивления,
- осевой момент сопротивления,  – осевой момент инерции,
– осевой момент инерции, 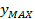 - расстояние по модулю до наиболее удалённой точки сечения от Ох.
- расстояние по модулю до наиболее удалённой точки сечения от Ох.
При косом изгибе МХ, МУ 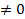 .
.
Уравнение нейтральной линии, т.е. геометрического места точек, где нормальное напряжение принимает нулевые значения, находят, полагая в (5.26) s = 0:
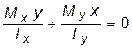 Откуда определяется:
Откуда определяется:  (5.27)
(5.27)
Эпюра напряжений в поперечных сечениях бруса линейна, следовательно, максимальные напряжения в сечении возникают в точках наиболее удаленных от нейтральной линии.
Расчёт на прочность при изгибе проводится при условиях:
1) материал работает одинаково на растяжение и сжатие, т.е. 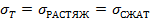
Условие прочности: 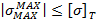 , где
, где 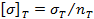 ,
, 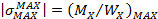 , где
, где 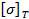 – допускаемое значение
– допускаемое значение
.
17. Условие прочности при кручении: прочность вала считается обеспеченной, если наибольшиекасательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых напряжений на кручение:
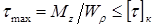
Формула служит для проверочного расчета вала на прочность.
Допускается незначительное (до 5 %) превышение расчетного напряжения 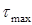 над допускаемым напряжением
над допускаемым напряжением 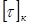 .
.
При проектировочном расчете требуемый полярный момент сопротивления определяется по формуле условия прочности при кручении:
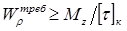 .
.
Для вала постоянного диаметра опасным сечением при кручении является сечение, в котором возникает наибольший крутящий момент. Если сечение вала не постоянно по длине, может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно.
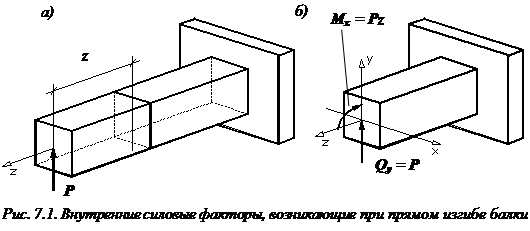
19. Рассмотрим, например, балку (рис. 7.1, а), нагруженную вертикальной сосредоточенной силой (P). Для определения внутренних усилий при прямом изгибе, возникающих в поперечном сечении, расположенном на расстоянии z от места приложения нагрузки, воспользуемся методом сечений.
 Разрежем мысленно балку в интересующем месте на две части.
Разрежем мысленно балку в интересующем месте на две части.
Отбросим левую часть балки, нагруженную силой P.
Заменим действие отброшенной левой части балки на оставленную правую часть внутренними силами.
Внутренние усилия возникают во всех точках поперечного сечения балки и распределены по неизвестному закону. Не имея возможности определить эти внутренние усилия для каждой точки сечения, заменяем их статически эквивалентными внутренними силовыми факторами, приложенными в центре тяжести поперечного сечения.
Внутренние силовые факторы определяются из условия равновесия рассматриваемой части балки. Однако можем внутренние силовые факторы найти и непосредственно, как действие отброшенной левой части на правую часть. Видно, что часть балки, нагруженная силой P, стремится изогнуть рассматриваемую нами правую часть выпуклостью вниз, а также пытается произвести срез. Следовательно, в сечении должны возникнуть поперечная сила 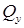 и изгибающий момент
и изгибающий момент 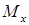 .
.
Осуществим параллельный перенос силы P в центр тяжести поперечного сечения балки. По правилам теоретической механики мы должны добавить момент, равный 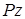 (рис. 7.1, б).
(рис. 7.1, б).
При прямом изгибе в поперечном сечении балки возникают два внутренних силовых фактора:
изгибающий момент, численно равный алгебраической сумме моментов всех сил, приложенных к отбрасываемой части балки, относительно главной центральной оси, проходящей через центр тяжести рассматриваемого сечения (в рассмотренном нами случае изгибающий момент равен: 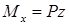 );
);
поперечная сила, численно равная алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки (в нашем случае поперечная сила равна: 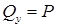 ).
).
Поперечный изгиб - изгиб, при котором в поперечном сечении балки возникают и изгибающий момент, и поперечная сила. Если поперечная сила не возникает, изгиб называется чистым изгибом.
21. Дифференциальные зависимости между распределенной нагрузкой, поперечной силой и изгибающим моментом:
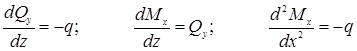
Дифференциальные зависимости используются для контроля правильности построенных эпюр поперечных сил 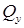 и изгибающих моментов
и изгибающих моментов 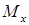 .
.
Помимо дифференциальных зависимостей существуют интегральные зависимости, получаемые из формул дифференциальных зависимостей. Например, изгибающий момент равен определенному интегралу по длине участка балки. Используя интегральную зависимость между изгибающим моментом и поперечной силой и аналитическое выражение поперечных сил, можно построить эпюру изгибающих моментов, не определяя выражение для них.
В формулах дифференциальных и интегральных зависимостей распределенная нагрузка (q) положительна, если направлена вниз.
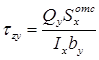 - формула Журавского
- формула Журавского
Формула Журавского получена в 1855 г. Д.И. Журавским, поэтому носит его имя.
Формула Журавского позволяет определить касательные напряжения при изгибе, возникающие в точках поперечного сечении балки, находящиеся на расстоянии от нейтральной оси x.
24. I тип задач: проверочный расчет. Выполняется по уравнениям.
Для хрупких материалов, если на эпюре изгибающих моментов имеются участки разных знаков, расчет на прочность выполняют для двух сечений: с наибольшими напряжениями сжатия и растяжения.
II тип задач: проектный расчет или подбор сечения.
Для подбора сечения из условия прочности выражается осевой момент сопротивления сечения:

Так как пластичные материалы одинаково работают на растяжение и на сжатие балки, сечения из таких материалов выполняют симметричными относительно оси Оx (швеллер, двутавр, прямоугольник).
Однако в этом случае материал, равномерно распределенный по высоте сечения, плохо используется в зоне нейтральной оси. Чтобы получить более рациональное сечение, необходимо возможно большую часть материала переместить в зоны, максимально удаленные от нейтральной оси. Таким образом, приходим к рациональному для пластичного материала сечению в форме симметричногодвутавра (рис. 7.3, б), у которого возможно большая часть материала сосредоточена на полках (горизонтальных массивных листах), соединенных стенкой (вертикальным листом), толщина которой δ назначается из условий прочности стенки по касательным напряжениям, а также из соображений ее устойчивости. К двутавровому сечению близко по критерию рациональности так называемое коробчатое сечение (рис.7.3, в).
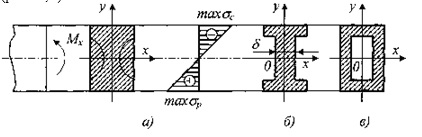 Хрупкие материалы хуже работают на растяжение и лучше на сжатие, поэтому балки из хрупких материалов выполняют несимметрично оси X (тавровые балки). Балку располагают так, чтобы большая ее площадь попала в область растянутых волокон:
Хрупкие материалы хуже работают на растяжение и лучше на сжатие, поэтому балки из хрупких материалов выполняют несимметрично оси X (тавровые балки). Балку располагают так, чтобы большая ее площадь попала в область растянутых волокон:

Из двух значений Wx принимаем большее значение.
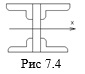
При проектировании составных балок (из нескольких элементов) необходимо расположить эти элементы так, чтобы они находились как можно дальше от центра тяжести балки (рис. 7.4).
III тип задач: определение допускаемой нагрузки.
Для пластичных материалов допускаемая нагрузка определяется по формуле:

Для хрупких материалов по формулам:
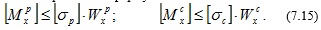
Из двух полученных значений допускаемых моментов выбирается меньший.
Определение напряжений при поперечном изгибе. При плоском поперечном изгибе в поперечном сечении балки от действия поперечной силы возникают касательные напряжения. На основании закона парности касательных напряжений они возникают также и в продольных сечениях. Вследствие чего происходит сдвиг одних продольных волокон относительно других. Попе-речные сечения при этом искривляются и гипотеза плоских сечений не выполняется. Однако на величину нормальных напряжений искривление поперечных сечений существенно не влияет. Поэтому они определяются по той же формуле, что и для чистого изгиба. Для вывода формулы касательных напряжений при изгибе рассмотрим консольную балку симметричного поперечного сечения, нагруженную силой. Эпюры приведены. Двумя поперечными сечениями выделим из балки бесконечно малый элемент длиной. Действие отброшенных частей балки заменим поперечными силами и изгибающими моментами. Изгибающий момент в правом сечении элемента на бесконечно малую величину больше, чем в левом, а поперечные силы в обоих сечениях одинаковы. Сечением, проведенным параллельно нейтральному слою на уровне, разделим элемент на две части. По продольному сечению балки возникают усилия сдвига, интенсивностью, благодаря которым устраняются относительные проскальзывания частей балки, соприкасающихся по продольному сечению, и балка работает на изгиб как сплошное монолитное тело, а эпюра изменяется по высоте сечения без скачков в соответствии с формулой.новесия верхней отсеченной части сечения. Преобразуя полученное выражение относительно касательного напряжения, получим формулу Журавского, касательные напряжения в продольных и поперечных сечениях балки поперечная сила в рассмотренном сечении, берется по эпюре со своим знаком статический момент отсеченной части относительно оси момент инерции всего сечения относительно оси
(Продолжение 24 –го вопроса)
ширина поперечного сечения балки на расстоянии от нейтральной оси. Знак касательного напряжения определяется знаком поперечной силы. Формула получена для касательных напряжений, возникающих в сечении параллельном нейтральному слою, но по закону парности касательных напряжений такие же напряжения возникают и в поперечных сечениях на расстоянии от нейтральной оси. Установим закон распределения касательных напряжений по высоте для прямоугольного поперечного сечения. Отсечем на расстоянии y часть сечения площадью, тогда центром тяжести верхней отсеченной части будет точка, ее координату определим как. Статический момент отсеченной части будет равен. Осевой момент инерции для прямоугольного сечения определяется по формуле. Подставляем выражения для и в формулу Журавского и получаем: В полученное выражение координата y входит в квадрате, следовательно, касательное напряжение изменяется по высоте сечения по параболическому закону. В крайних точках сечения. В точках нулевой линии.
8. Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
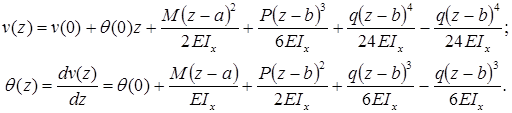
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
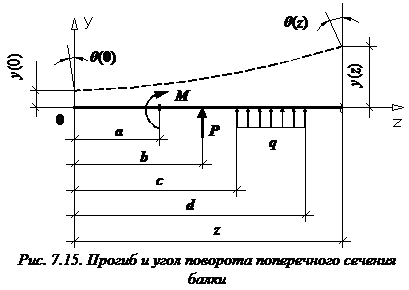
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб 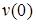 и угол поворота
и угол поворота 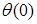 балки в начале координат (начальные параметры) определяются из условий закрепления балки.
балки в начале координат (начальные параметры) определяются из условий закрепления балки.
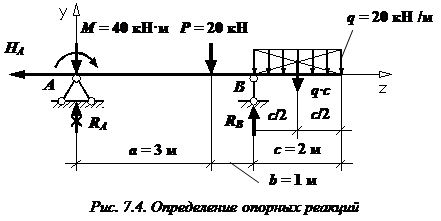
Определим прогиб балки на консоли при 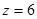 м, то есть
м, то есть 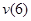 . Запишем универсальное уравнение упругой линии балки:
. Запишем универсальное уравнение упругой линии балки:
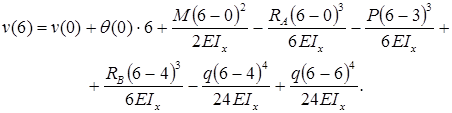
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: 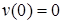 .
.
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
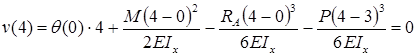 ,
,
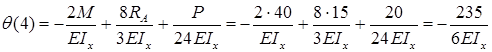 .
.
Продолжение (8-го вопроса)
Прогиб консоли при z=6м:
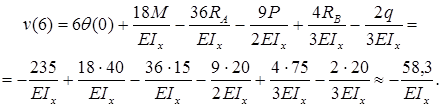
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
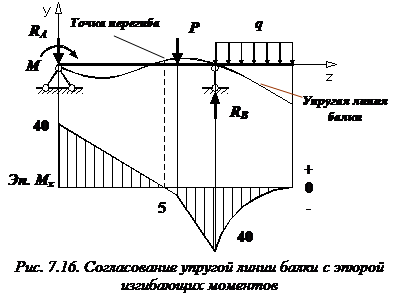
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов подифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
15. Крутящие моменты, о которых шла речь выше, представляют лишь равнодействующие внутренние усилия. Фактически в поперечном сечении скручиваемого стержня действуют непрерывно распределенные внутренние касательные напряжения, к определению которых теперь и перейдем.
Ознакомимся прежде всего с результатами опытов. Если на поверхность стержня круглого сечения нанести прямоугольную сетку, то после деформации окажется (рис. 2.6):
1) прямоугольная сетка превратится в сетку, состоящую из параллелограммов, что свидетельствует о наличии касательных напряжений в поперечных сечениях бруса, а по закону парности касательных напряжений - и в продольных его сечениях;
2) расстояния между окружностями, например между I и II, не изменятся. Не изменится длина стержня и его диаметр. Естественно допустить, что каждое поперечное сечение поворачивается в своей плоскости на некоторый угол, как жесткое целое (гипотеза плоских и жестких сечений). На основании этой гипотезы можно считать, что радиусы всех поперечных сечений будут поворачиваться (на равные углы), оставаясь прямолинейными.
На основании этого можно принять, что при кручении в поперечных сечениях стержня действуют только касательные напряжения, т.е. напряженное состояние в точках скручиваемого стержня представляет собой чистый сдвиг.
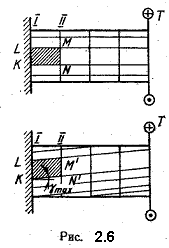 Формулы, полученные на основе этого допущения, подтверждаются опытами. Точка D переместится по дуге DD', точка C – поменьшей дуге CC'
Формулы, полученные на основе этого допущения, подтверждаются опытами. Точка D переместится по дуге DD', точка C – поменьшей дуге CC'

Для установления закона распределения касательных напряжений по поперечному сечению скручиваемого стержня рассмотрим более детально деформации стержня (рис. 2.6 и 2.8). На рис. 2.8 в более крупном масштабе изображена часть стержня между сечениями I и II и показана одна сторона KN элемента KLMN (рис. 2.6).
Угол сдвига для элемента KLMN, лежащего на поверхности стержня, равен отношению отрезка NN' к длине элемента dz (см. рис. 2.8)
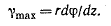 Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса p и повторяя те же рассуждения, получим угол сдвига для элемента, отстоящего на расстоянии p от оси стержня
Выделяя мысленно из рассматриваемой части бруса цилиндр произвольного радиуса p и повторяя те же рассуждения, получим угол сдвига для элемента, отстоящего на расстоянии p от оси стержня
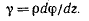 на основании закона Гука при сдвиге имеем
на основании закона Гука при сдвиге имеем
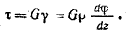 Как видим, при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.
Как видим, при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения.
Эпюра касательных напряжений по поперечному сечению стержня представлена на рис. 2.7 справа.
(Продолжение 15-го вопроса)
В центре тяжести круглого сечения касательные напряжения равны нулю. Наибольшие касательные напряжения будут в точах сечения, расположенных у поверхности стержня.
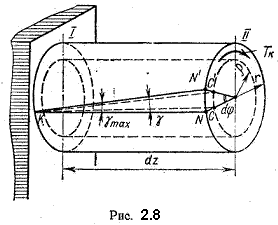
Зная закон распределения касательных напряжений, легко определить их величину из учловия, что крутящий момент в сечении представляет собой равнодействующий момент касательных напряжений в сечении:
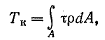 где ТрdA - элементарный крутящий момент внутренних сил, действующий по площадке dA.
где ТрdA - элементарный крутящий момент внутренних сил, действующий по площадке dA.
Подставив в (2.4) значение напряжений из формулы (2.3) получим
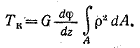 Имея ввиду, что
Имея ввиду, что
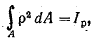 где Ip - полярный момент инерции сечения, получим
где Ip - полярный момент инерции сечения, получим
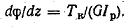 Подставляя значение
Подставляя значение 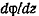 в формулу (2.3), имеем
в формулу (2.3), имеем
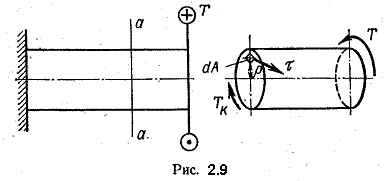
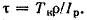 В частном случае, когда на стержень действует один внешний скручивающий момент Т (рис. 2.9), из условия равновесия отсеченной части стержня получим Тк = Т.
В частном случае, когда на стержень действует один внешний скручивающий момент Т (рис. 2.9), из условия равновесия отсеченной части стержня получим Тк = Т.
Таким образом, окончательная формула для определения касательных напряжений при кручении имеет вид
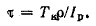 Как видно из этой формулы, в точках, одинаково удаленных от центра сечения, напряжения
Как видно из этой формулы, в точках, одинаково удаленных от центра сечения, напряжения 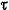 одинаковы.
одинаковы.
Наибольшие напряжения в точках у контура сечения равны
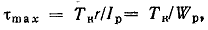
где
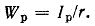 Геометрическая характеристика Wp называется полярным моментом сопротивления или моментом сопротивления при кручении.
Геометрическая характеристика Wp называется полярным моментом сопротивления или моментом сопротивления при кручении.
Для круглого сплошного сечения
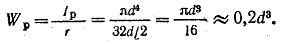
Для колцевогосечения
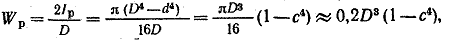 где c = d/D.
где c = d/D.
Условие статической прочности вала при кручении имеет вид
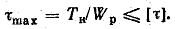 Здесь
Здесь 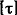 - допускаемое касательное напряжение.
- допускаемое касательное напряжение.
При действии статической нагрузки принимают (без учета концентрации напряжений и других факторов, снижающих прочность)
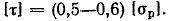 Кроме проверки прочности, по этой формуле можно также подбирать диаметр вала или определять допускаемыйкрутящий момент при известных остальных величинах.
Кроме проверки прочности, по этой формуле можно также подбирать диаметр вала или определять допускаемыйкрутящий момент при известных остальных величинах.
Имея в виду, что для круглого сплошного сечения 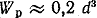 , получаем
, получаем
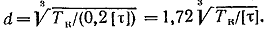 По этой формуле определяют диаметр вала из условия прочности.
По этой формуле определяют диаметр вала из условия прочности.
Допускаемый из условия прочности крутящий момент определяют по формуле
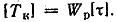 Касательные напряжения действуют не только в
Касательные напряжения действуют не только в
(Продолжение 15-го вопроса)
поперечных сечениях стержня, но и (как это следует из закона парности касательных напряжений) в продольных сечениях (рис. 2.10).
В наклонных же сечениях стержня действуют и нормальные и касательные напряжения. Они могут быть вычислены.
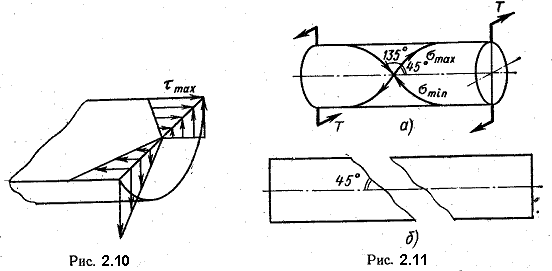
Опыты показывают, что хрупкие материалы, например чугун, при кручении разрушаются по плоскости (говоря точнее, по винтовой поверхности), наклоненной к оси вала под углом 45 градусов (рис. 2.11, б), т.е. по тем плоскостям, где действуют наибольшие растягивающие напряжения.
Следовательно, при кручении во всех точках стержня, кроме точек его оси (в которых вообще не возникает напряжений), имеет место двухосное напряженное состояние - чистый сдвиг. При кручении материал у поверхности стержня напряжен сильнее, чем материал, расположенный, ближе к оси стержня. Таким образом, напряженное состояние является неоднородным. Если же скручивать тонкостенную трубу, то можно считать, что практически во всех точках ее стенки возникают одинаковые напряжения, т.е. в этом случае напряженное состояние будет однородным. Опыты с кручением таких труб используют обычно для изучения чистого сдвига и, в частности, для установления предела текучести при сдвиге 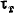 .
.
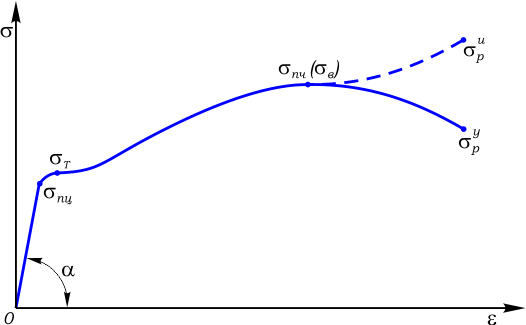 По этой диаграмме определяются следующие механические характеристики материала: σ пц - предел пропорциональности
Определяется как крайняя верхняя точка начального прямолинейного участка диаграммы.
σ пц = Fпц / A0 σ Т - предел текучести
Точка после которой линия диаграммы некоторое время движется параллельно осидеформаций ε.
Практически горизонтальный участок диаграммы, следующий за пределом текучести называется площадкой текучести.
σ Т = FТ / A0 σ пч - предел прочности (σ в - временное сопротивление)
Высшая точка условной диаграммы;
σ пч = Fmax / A0 σ р - напряжение в момент разрыва образца (σ ру - условное и σ ри - истинное)
Конечная точка диаграммы, при которой происходит разрыв образца.
- условное напряжение разрываσ ру = Fр / A0
- истинное напряжение при разрывеσ ри = Fр / Aш
здесь Aш - площадь поперечного сечения в области " шейки" образца.
При более тонких испытаниях по данной диаграмме можно определить предел упругостистали.
На рисунке 1 штриховой линией показан фрагмент истинной диаграммы напряжений. Возрастание напряжений после прохождения предела прочности объясняется тем, что в этот момент в рабочей части образца образуется локальное утоньшение (" шейка") уменьшаюшая его плошадь поперечного сечения A, что в свою очередь приводит к увеличению напряжений при уменьшении растягивающей силы.
Кроме того, по диаграмме напряжений можно приближенно определить величину модуля упругости I рода материала образца:
E=σ /ε =tgα
он определяется как отношение напряжений и относительных деформаций, для любой точки диаграммы расположенной от ее начала до предела пропорциональности, либо как тангенс угла наклона начального участка диаграммы к оси ε.
7.Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов). Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
10. Абсолютная деформация выражает абсолютное изменение какого-либо линейного или углового размера, площади сечения или участка граничной поверхности элемента, выделенного в деформируемом теле, или всего тела.
Относительная деформация характеризует относительное изменение тех же величин. Обычно относительную деформацию определяют как отношение абсолютного изменения какого-либо размера к его первоначальному значению.
Абсолютная деформация при осадке ∆ H = H - h. (см. рис. 1.4) не характеризует степени воздействия деформации на металл, что видно из следующего примера.
Пусть первая заготовка имеет начальную высоту Н, равную 1000 мм, вторая — 500 мм. Осадим каждую из них до половины начальной высоты, т. е. величина абсолютной деформации ∆ H составит для первой заготовки 500 мм, для второй — 250 мм.
Относительную деформацию в процентах для обеих заготовок подсчитаем по формуле є= (H-h') / H*100
Подставив числовые значения H u h, получим для первого и второго случаев одинаковую относительную деформацию, равную 50%, что свидетельствует об одинаковой степени воздействия деформации на металл при разных ее абсолютных значениях.
Для операции протяжки при ковке величина пластической деформации металла характеризуется уковом У= Fн/ Fк, где Fн и Fк- площади поперечных сечений соответственно заготовки и поковки.
Вытяжка μ при протяжке представляет собой отношение длины поковки Lк к длине заготовки Lн. Если поковка имеет по всей длине постоянное поперечное сечение, вытяжка и уковравны друг другу.
Абсолютное удлинение (укорочение) бруса (стержня) выражается формулой:
По этой диаграмме определяются следующие механические характеристики материала: σ пц - предел пропорциональности
Определяется как крайняя верхняя точка начального прямолинейного участка диаграммы.
σ пц = Fпц / A0 σ Т - предел текучести
Точка после которой линия диаграммы некоторое время движется параллельно осидеформаций ε.
Практически горизонтальный участок диаграммы, следующий за пределом текучести называется площадкой текучести.
σ Т = FТ / A0 σ пч - предел прочности (σ в - временное сопротивление)
Высшая точка условной диаграммы;
σ пч = Fmax / A0 σ р - напряжение в момент разрыва образца (σ ру - условное и σ ри - истинное)
Конечная точка диаграммы, при которой происходит разрыв образца.
- условное напряжение разрываσ ру = Fр / A0
- истинное напряжение при разрывеσ ри = Fр / Aш
здесь Aш - площадь поперечного сечения в области " шейки" образца.
При более тонких испытаниях по данной диаграмме можно определить предел упругостистали.
На рисунке 1 штриховой линией показан фрагмент истинной диаграммы напряжений. Возрастание напряжений после прохождения предела прочности объясняется тем, что в этот момент в рабочей части образца образуется локальное утоньшение (" шейка") уменьшаюшая его плошадь поперечного сечения A, что в свою очередь приводит к увеличению напряжений при уменьшении растягивающей силы.
Кроме того, по диаграмме напряжений можно приближенно определить величину модуля упругости I рода материала образца:
E=σ /ε =tgα
он определяется как отношение напряжений и относительных деформаций, для любой точки диаграммы расположенной от ее начала до предела пропорциональности, либо как тангенс угла наклона начального участка диаграммы к оси ε.
7.Диаграмма растяжения показывает зависимость удлинения образца от продольной растягивающей силы.Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном металлов). Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.Для этого образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до их полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
10. Абсолютная деформация выражает абсолютное изменение какого-либо линейного или углового размера, площади сечения или участка граничной поверхности элемента, выделенного в деформируемом теле, или всего тела.
Относительная деформация характеризует относительное изменение тех же величин. Обычно относительную деформацию определяют как отношение абсолютного изменения какого-либо размера к его первоначальному значению.
Абсолютная деформация при осадке ∆ H = H - h. (см. рис. 1.4) не характеризует степени воздействия деформации на металл, что видно из следующего примера.
Пусть первая заготовка имеет начальную высоту Н, равную 1000 мм, вторая — 500 мм. Осадим каждую из них до половины начальной высоты, т. е. величина абсолютной деформации ∆ H составит для первой заготовки 500 мм, для второй — 250 мм.
Относительную деформацию в процентах для обеих заготовок подсчитаем по формуле є= (H-h') / H*100
Подставив числовые значения H u h, получим для первого и второго случаев одинаковую относительную деформацию, равную 50%, что свидетельствует об одинаковой степени воздействия деформации на металл при разных ее абсолютных значениях.
Для операции протяжки при ковке величина пластической деформации металла характеризуется уковом У= Fн/ Fк, где Fн и Fк- площади поперечных сечений соответственно заготовки и поковки.
Вытяжка μ при протяжке представляет собой отношение длины поковки Lк к длине заготовки Lн. Если поковка имеет по всей длине постоянное поперечное сечение, вытяжка и уковравны друг другу.
Абсолютное удлинение (укорочение) бруса (стержня) выражается формулой:
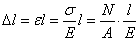 , т.е.
, т.е. 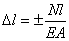 Учитывая, что величина
Учитывая, что величина 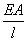 представляет собой жесткость поперечного сечения бруса длиной
представляет собой жесткость поперечного сечения бруса длиной  можно сделать вывод: абсолютная продольная деформация прямо пропорциональна продольной силе и обратно пропорциональна жесткости поперечного сечения. Этот закон впервые сформулировал Гук в 1660 году.
12.Из курса физики известно, что при повышении температуры линейные размеры тела увеличиваются, а при охлаждении— уменьшаются.
В случае если при нагреве (охлаждении) стержня ничто не препятствует изменению его длины, в нем не возникает никаких напряжений. Например, при нагревании.стержня ВС, поддерживающего шарнирно закрепленную одним концом балку, он удлиняется, вызывая поворот балки вокруг шарнира А.
Иное положение в статически неопределимых системах. Если нагреть стержень ВС статически неопределимой системы, изображенной на, то его свободному удлинению, а вместе с тем и повороту балки (считаем ее абсолютно жесткой) препятствует стержень DK. В результате в стержне ВС возникает сжатие и опускание точки В будет меньше, чем свободное температурное удлинение (Ы,) стержня. При этом стержень DK испытывает растяжение.
В задачах на температурные напряжения особенно важно четко разграничивать понятия «растяжение» и «удлинение», «сжатие» и «укорочение». Так, в рассмотренном примере стержень ВС хотя и удлиняется, но испытывает при этом сжатие.
Таким образом, изменение температуры статически неопределимой системы (или отдельных ее частей) вызывает напряжения в ее элементах (температурные напряжения).
Существует еще один вид напряжений, которые характерны только для статически неопределимых систем. Это так называемые начальныеили монтажные напряжения.
Причиной их возникновения может, в частности, явиться неточность изготовления отдельных элементов конструкции.
Сокращаясь (в силу своей упругости), стержень несколько приподнимет конец балки, что вызовет сжатиестержня DK. В статически определимой системе неточность изготовления ее элементов напряжений не вызовет. Начальнымисоответствующие напряжения называют потому, что они возникают в конструкции до приложений к ней рабочих нагрузок.
16. В опасном сечении вала при изгибе с кручением одновременно возникают наибольшие крутящий (
можно сделать вывод: абсолютная продольная деформация прямо пропорциональна продольной силе и обратно пропорциональна жесткости поперечного сечения. Этот закон впервые сформулировал Гук в 1660 году.
12.Из курса физики известно, что при повышении температуры линейные размеры тела увеличиваются, а при охлаждении— уменьшаются.
В случае если при нагреве (охлаждении) стержня ничто не препятствует изменению его длины, в нем не возникает никаких напряжений. Например, при нагревании.стержня ВС, поддерживающего шарнирно закрепленную одним концом балку, он удлиняется, вызывая поворот балки вокруг шарнира А.
Иное положение в статически неопределимых системах. Если нагреть стержень ВС статически неопределимой системы, изображенной на, то его свободному удлинению, а вместе с тем и повороту балки (считаем ее абсолютно жесткой) препятствует стержень DK. В результате в стержне ВС возникает сжатие и опускание точки В будет меньше, чем свободное температурное удлинение (Ы,) стержня. При этом стержень DK испытывает растяжение.
В задачах на температурные напряжения особенно важно четко разграничивать понятия «растяжение» и «удлинение», «сжатие» и «укорочение». Так, в рассмотренном примере стержень ВС хотя и удлиняется, но испытывает при этом сжатие.
Таким образом, изменение температуры статически неопределимой системы (или отдельных ее частей) вызывает напряжения в ее элементах (температурные напряжения).
Существует еще один вид напряжений, которые характерны только для статически неопределимых систем. Это так называемые начальныеили монтажные напряжения.
Причиной их возникновения может, в частности, явиться неточность изготовления отдельных элементов конструкции.
Сокращаясь (в силу своей упругости), стержень несколько приподнимет конец балки, что вызовет сжатиестержня DK. В статически определимой системе неточность изготовления ее элементов напряжений не вызовет. Начальнымисоответствующие напряжения называют потому, что они возникают в конструкции до приложений к ней рабочих нагрузок.
16. В опасном сечении вала при изгибе с кручением одновременно возникают наибольшие крутящий (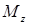 ) и результирующий изгибающий
) и результирующий изгибающий 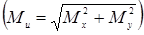 момент.
момент.
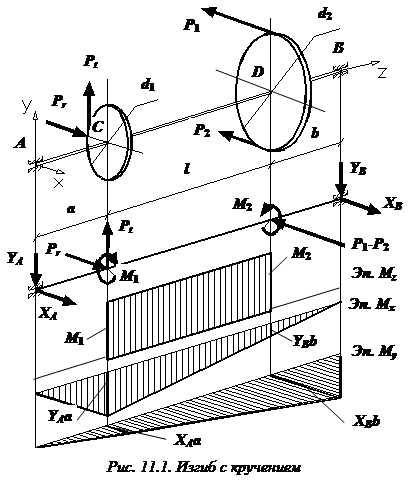 В рассматриваемом примере (рис. 11.1) опасным является либо поперечное сечение, расположенное чуть правее точки С, либо чуть левее точки D (в зависимости от того, какой из изгибающих моментов: больше
В рассматриваемом примере (рис. 11.1) опасным является либо поперечное сечение, расположенное чуть правее точки С, либо чуть левее точки D (в зависимости от того, какой из изгибающих моментов: больше 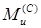 или
или 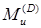 ).
Опасным является то сечение, в котором эквивалентный момент будет наибольшим.
Опасные точки – это 2 точки поперечного сечения, в которых одновременно нормальные напряжения от изгиба и касательные напряжения от кручения имеют наибольшие значения. Опасные точки расположены вблизи контура поперечного сечения вала. Поскольку валы, как правило, изготавливают из пластичного материала, обе опасные точки равноопасны.
(Продолждение 11-го вопроса)
предела текучести,
).
Опасным является то сечение, в котором эквивалентный момент будет наибольшим.
Опасные точки – это 2 точки поперечного сечения, в которых одновременно нормальные напряжения от изгиба и касательные напряжения от кручения имеют наибольшие значения. Опасные точки расположены вблизи контура поперечного сечения вала. Поскольку валы, как правило, изготавливают из пластичного материала, обе опасные точки равноопасны.
(Продолждение 11-го вопроса)
предела текучести, 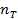 - коэф. запаса.
2) если неодинаково, то работают два условия:
- коэф. запаса.
2) если неодинаково, то работают два условия:
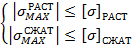 , где
, где 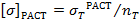 ,
, 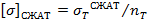 Если расчёт проектировочный, то из двух коэффициентов выбирется наибольший. В поверочном – наоборот.
В целях безопасной работы напряжения должны быть ниже предельных значений для данного материала. Таким образом при поверочном расчёте (нахожд. Нормативного коэф. запаса):
Если расчёт проектировочный, то из двух коэффициентов выбирется наибольший. В поверочном – наоборот.
В целях безопасной работы напряжения должны быть ниже предельных значений для данного материала. Таким образом при поверочном расчёте (нахожд. Нормативного коэф. запаса):
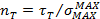 , где
, где 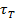 - предельное кас. напряжение материала, nТ – коэф. запаса,
за расчётный коэффициент принимают [n] > nТ, где [n] – нормативный (предписываемый нормами проектирования конструкций) коэф. запаса.
Продолжение 17-го вопроса
Допускаемое напряжение
- предельное кас. напряжение материала, nТ – коэф. запаса,
за расчётный коэффициент принимают [n] > nТ, где [n] – нормативный (предписываемый нормами проектирования конструкций) коэф. запаса.
Продолжение 17-го вопроса
Допускаемое напряжение 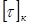 :
для пластичных материалов назначается в зависимости от предела текучести (
:
для пластичных материалов назначается в зависимости от предела текучести (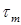 ) при кручении(сдвиге):
) при кручении(сдвиге):
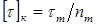 .
для хрупких материалов назначается в зависимости от предела прочности:
.
для хрупких материалов назначается в зависимости от предела прочности:
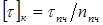 .
20. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
Определение поперечных сил и изгибающих моментов - сечение 1
Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой
.
20. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ
Определение поперечных сил и изгибающих моментов - сечение 1
Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой 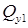 и изгибающим моментом
и изгибающим моментом 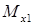 . Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.
Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия
Видим только реакцию опоры, направленную вниз. Таким образом, поперечная сила равна:
. Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.
Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия
Видим только реакцию опоры, направленную вниз. Таким образом, поперечная сила равна:
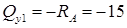 кН.
Знак «минус» нами взят потому, что сила
кН.
Знак «минус» нами взят потому, что сила 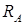 вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)
Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.
вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)
Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.
 Видим два усилия: реакцию опоры
Видим два усилия: реакцию опоры 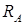 и момент M. Однако у силы
и момент M. Однако у силы 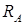 плечо практически равно нулю. Поэтомуизгибающий моментравен:
плечо практически равно нулю. Поэтомуизгибающий моментравен:
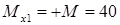 кН·м.
Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков)
Определение поперечных сил и изгибающих моментов - сечение 2
В отличие от первого сечения, у силы реакции
кН·м.
Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков)
Определение поперечных сил и изгибающих моментов - сечение 2
В отличие от первого сечения, у силы реакции 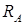 появилось плечо, равное а.
поперечная сила:
появилось плечо, равное а.
поперечная сила:
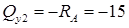 кН;
изгибающий момент:
кН;
изгибающий момент:
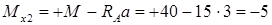 кН·м.
Определение поперечных сил и изгибающих моментов - сечение 3
поперечная сила:
кН·м.
Определение поперечных сил и изгибающих моментов - сечение 3
поперечная сила:
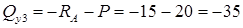 кН;
изгибающий момент:
кН;
изгибающий момент:
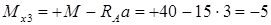 кН ·м.
Определение поперечных сил и изгибающих моментов - сечение 4
Теперь удобнее закрывать листком левую часть балки.
поперечная сила:
кН ·м.
Определение поперечных сил и изгибающих моментов - сечение 4
Теперь удобнее закрывать листком левую часть балки.
поперечная сила:
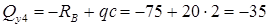 кН;
изгибающий момент:
кН;
изгибающий момент:
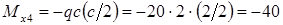 кН ·м.
(Продолжение 20-го вопроса)
Определение поперечных сил и изгибающих моментов - сечение 5
поперечная сила:
кН ·м.
(Продолжение 20-го вопроса)
Определение поперечных сил и изгибающих моментов - сечение 5
поперечная сила:
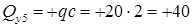 кН;
изгибающий момент:
кН;
изгибающий момент:
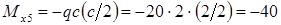 кН ·м.
Определение поперечных сил и изгибающих моментов - сечение 1
поперечная сила и изгибающий момент:
кН ·м.
Определение поперечных сил и изгибающих моментов - сечение 1
поперечная сила и изгибающий момент:
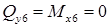 .
По найденным значениям производим построение эпюры поперечных сил
.
По найденным значениям производим построение эпюры поперечных сил 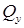 (рис. 7.7, б) и изгибающих моментов
(рис. 7.7, б) и изгибающих моментов 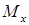 (рис. 7.7, в).
Проверка эпюры поперечных сил
Убеждаемся: под незагруженными участками эпюра поперечных сил идет параллельно оси балки, а под распределенной нагрузкой q –
(Продолжение 20-го вопроса)
по наклоненной вниз прямой. На эпюре продольной силы
(рис. 7.7, в).
Проверка эпюры поперечных сил
Убеждаемся: под незагруженными участками эпюра поперечных сил идет параллельно оси балки, а под распределенной нагрузкой q –
(Продолжение 20-го вопроса)
по наклоненной вниз прямой. На эпюре продольной силы 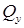 три скачка: под реакцией
три скачка: под реакцией 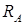 – вниз на 15 кН, под силой P – вниз на 20 кН и под реакцией
– вниз на 15 кН, под силой P – вниз на 20 кН и под реакцией 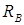 – вверх на 75 кН.
Проверка эпюры изгибающих моментов
На эпюре изгибающих моментов видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изгибающих моментов изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре изгибающего момента
– вверх на 75 кН.
Проверка эпюры изгибающих моментов
На эпюре изгибающих моментов видим изломы под сосредоточенной силой P и под опорными реакциями. Углы изломов направлены навстречу этим силам. Под распределенной нагрузкой q эпюра изгибающих моментов изменяется по квадратичной параболе, выпуклость которой направлена навстречу нагрузке. В сечении 6 на эпюре изгибающего момента 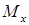 – экстремум, поскольку эпюра поперечной силы в этом месте проходит через нулевое значение
23. При поперечном изгибе наряду с изгибающим моментом в сечении балки возникает поперечная сила (Q). Наличие поперечной силы связано с возникновением в поперечном сечении касательных напряжений.
Русский инженер – мостостроитель Дмитрий Иванович Журавский в связи с проектированием деревянных мостов для ж/д Петербург – Москва проводил исследования определения и изменения касательных напряжений при поперечном изгибе и разработал в 1844-1850гг. теорию касательных напряжений в балках прямоугольного профиля. Им было установлено, что касательное напряжение при изгибе не распределяются равномерно на высоте сечения. Также он получил формулу для подсчета касательных напряжений при изгибе, которая носит название формулы Журавского.
τ =
– экстремум, поскольку эпюра поперечной силы в этом месте проходит через нулевое значение
23. При поперечном изгибе наряду с изгибающим моментом в сечении балки возникает поперечная сила (Q). Наличие поперечной силы связано с возникновением в поперечном сечении касательных напряжений.
Русский инженер – мостостроитель Дмитрий Иванович Журавский в связи с проектированием деревянных мостов для ж/д Петербург – Москва проводил исследования определения и изменения касательных напряжений при поперечном изгибе и разработал в 1844-1850гг. теорию касательных напряжений в балках прямоугольного профиля. Им было установлено, что касательное напряжение при изгибе не распределяются равномерно на высоте сечения. Также он получил формулу для подсчета касательных напряжений при изгибе, которая носит название формулы Журавского.
τ = 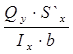 Qy (Q) – поперечная сила в рассматриваемом сечении.
S`x – статистический момент относительно нейтральной оси той части сечения, которая лежит выше или ниже прямой проведенной через данную точку;
Ix – осевой момент инерции всего сечения относительно нейтральной оси.
b – ширина поперечного сечения на уровне точки, в которой определяется напряжение.
Q, Ix, b для сечения постоянной ширины не меняются.
Sx изменяется в зависимости от y1 следовательно τ в любой точке поперечного сечения зависит только от y1. Касательные напряжения достигают максимального значения:
Для прямоугольного сечения: τ max =
Qy (Q) – поперечная сила в рассматриваемом сечении.
S`x – статистический момент относительно нейтральной оси той части сечения, которая лежит выше или ниже прямой проведенной через данную точку;
Ix – осевой момент инерции всего сечения относительно нейтральной оси.
b – ширина поперечного сечения на уровне точки, в которой определяется напряжение.
Q, Ix, b для сечения постоянной ширины не меняются.
Sx изменяется в зависимости от y1 следовательно τ в любой точке поперечного сечения зависит только от y1. Касательные напряжения достигают максимального значения:
Для прямоугольного сечения: τ max = 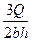 в точках на нейтральной линии, т. е. при y = 0.
Для двутавра: τ max =
в точках на нейтральной линии, т. е. при y = 0.
Для двутавра: τ max = 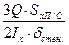 , где SxП/С – статистический момент полусечения.
Для круглого сечения: τ max =
, где SxП/С – статистический момент полусечения.
Для круглого сечения: τ max = 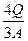 , где A – площадь.
Максимальное касательное напряжение для большинства симметричных сечений относительно нейтральной оси (X) имеет место в точках лежащих на нейтральной оси.
Для стальных балок [τ ] ≈ 0, 6∙ [σ ]
Условие прочности по касательным напряжениям: τ max ≤ [τ ]
При выводе формулы Журавского предполагалось: балка имеет прямоугольное поперечное сечение (рис. 7.11), поэтому
, где A – площадь.
Максимальное касательное напряжение для большинства симметричных сечений относительно нейтральной оси (X) имеет место в точках лежащих на нейтральной оси.
Для стальных балок [τ ] ≈ 0, 6∙ [σ ]
Условие прочности по касательным напряжениям: τ max ≤ [τ ]
При выводе формулы Журавского предполагалось: балка имеет прямоугольное поперечное сечение (рис. 7.11), поэтому
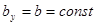 ;
; 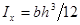 ;
; 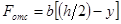 ;
; 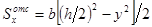 где y – расстояние от точки, в которой определяется касательное напряжение, до нейтральной оси x.
Подставляя эти формулы в формулу Журавского, длякасательныхнапряженийполучим:
(Продолжение 23 –го вопроса)
где y – расстояние от точки, в которой определяется касательное напряжение, до нейтральной оси x.
Подставляя эти формулы в формулу Журавского, длякасательныхнапряженийполучим:
(Продолжение 23 –го вопроса)
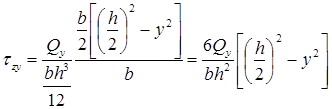 Касательные напряжения изменяются по высоте поперечного сечения по закону квадратичной параболы (см. рис. 7.11).
При
Касательные напряжения изменяются по высоте поперечного сечения по закону квадратичной параболы (см. рис. 7.11).
При 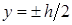 (для наиболее удаленных от нейтральной оси точек)
(для наиболее удаленных от нейтральной оси точек) 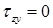 .
Для точек, расположенных на нейтральной оси (при
.
Для точек, расположенных на нейтральной оси (при 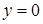 ),
), 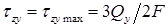 .
.
 14. Стержень испытывает кручение, если в его поперечных сечениях возникают крутящие моменты, т.е. моменты, лежащие в плоскости сечения. Обычно эти крутящие моменты Тк возникают под действием внешних моментов Т (рис. 2.1). Внешние моменты передаются на вал, как правило, в местах посадки на него шкивов, зубчатых колес и т.п.
Однако и поперечная нагрузка, смещенная относительно оси стержня, вызывает крутящие моменты (рис. 2.2), но в указанномслечае
14. Стержень испытывает кручение, если в его поперечных сечениях возникают крутящие моменты, т.е. моменты, лежащие в плоскости сечения. Обычно эти крутящие моменты Тк возникают под действием внешних моментов Т (рис. 2.1). Внешние моменты передаются на вал, как правило, в местах посадки на него шкивов, зубчатых колес и т.п.
Однако и поперечная нагрузка, смещенная относительно оси стержня, вызывает крутящие моменты (рис. 2.2), но в указанномслечае 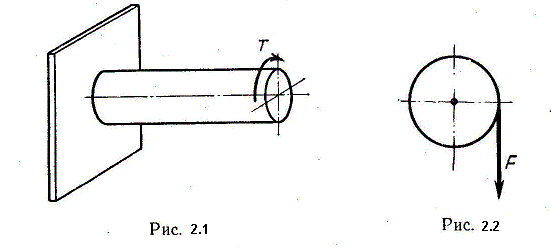 в поперечных сечениях наряду с крутящими моментами возникают и другие внутренние усилия - поперечные силы и изгибающие моменты.
Вращающиеся и работающие на кручение стержни называют валами.
Вместо аксонометрического изображения будем применять главным образом плоское, как более простое. Внешние скручивающие моменты и внутренние крутящие моменты будем изображать в виде линии с двумя кружочками. В одном из них будем ставить точку, обозначающую начало стрелки (на нас), в другом - крестик, обозначающий конец стрелки, направленный от нас (рис. 2.3).
Для определения крутящих моментов Тк возникающих в сечениях вала под действием внешних скручивающих моментов или поперечной нагрузки, будем применять метод сечений. Сделаем мысленный разрез стержня (рис. 2.3), например по а - а, отбросим одну часть стержня, в данном случае левую, и рассмотрим равновесие оставшейся правой части.
в поперечных сечениях наряду с крутящими моментами возникают и другие внутренние усилия - поперечные силы и изгибающие моменты.
Вращающиеся и работающие на кручение стержни называют валами.
Вместо аксонометрического изображения будем применять главным образом плоское, как более простое. Внешние скручивающие моменты и внутренние крутящие моменты будем изображать в виде линии с двумя кружочками. В одном из них будем ставить точку, обозначающую начало стрелки (на нас), в другом - крестик, обозначающий конец стрелки, направленный от нас (рис. 2.3).
Для определения крутящих моментов Тк возникающих в сечениях вала под действием внешних скручивающих моментов или поперечной нагрузки, будем применять метод сечений. Сделаем мысленный разрез стержня (рис. 2.3), например по а - а, отбросим одну часть стержня, в данном случае левую, и рассмотрим равновесие оставшейся правой части. 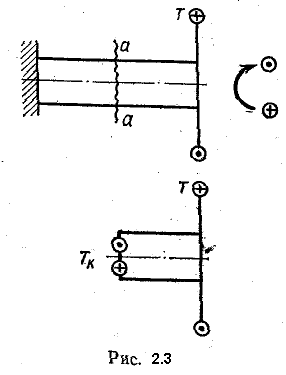 Взаимодействие частей стержня заменим крутящим моментом Тк, уравновешивающим внешний момент Т. Для равновесия отсеченной части необходимо, чтобы алгебраическая сумма всех моментов, действующих на нее, была равна нулю. Отсюда в рассматриваемом случае получим, что Тк = Т. Если на отсеченную часть будет
(Продолжение 14-го вопроса)
действовать несколько внешних моментов, то, проведя аналогичное рассуждения, можно убедиться, что крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения.
Для наглядного представления о характере распределения и величине крутящих моментов по длине стержня строят эпюры (графики) этих моментов. Построение их вполне аналогично построению эпюр продольных сил при растяжении или сжатии. Для построения эпюр необходимо условиться о правиле знаков. Общепринятого правила знаков для крутящих моментов не существует. Может быть принято любое правило знаков. Важно лишь принятое правило выдержать на всем протяжении эпюры.
Взаимодействие частей стержня заменим крутящим моментом Тк, уравновешивающим внешний момент Т. Для равновесия отсеченной части необходимо, чтобы алгебраическая сумма всех моментов, действующих на нее, была равна нулю. Отсюда в рассматриваемом случае получим, что Тк = Т. Если на отсеченную часть будет
(Продолжение 14-го вопроса)
действовать несколько внешних моментов, то, проведя аналогичное рассуждения, можно убедиться, что крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения.
Для наглядного представления о характере распределения и величине крутящих моментов по длине стержня строят эпюры (графики) этих моментов. Построение их вполне аналогично построению эпюр продольных сил при растяжении или сжатии. Для построения эпюр необходимо условиться о правиле знаков. Общепринятого правила знаков для крутящих моментов не существует. Может быть принято любое правило знаков. Важно лишь принятое правило выдержать на всем протяжении эпюры. 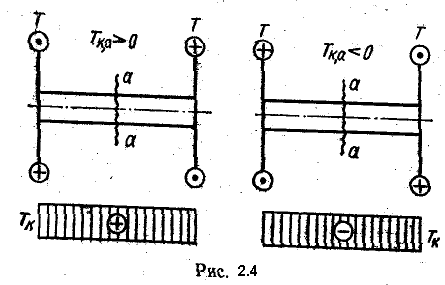 Примем следующее правило знаков (рис. 2.4). Крутящий момент в сечении а - а считается положительным, когда внешний момент вращает отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным.
Построение эпюры крутящих моментов поясним на следующем примере (рис. 2.5): рассмотрим вал CD, опирающийся на подшипники B и A и находящийся в равновесии под действием приложенных к нему в сечениях E, K и L моментов. Сделав сечение а - а где-либо на участке DL и рассмотрев равновесие правой отсеченной части, убедимся, что Тк = 0. Если мы сделаем затем сечение b - b в любом месте участка LK, то из условия равновесия правой от сечения части получим Тк = 20 кН * м.
Момент считаем положительным в соответствии с принятым правилом знаков. Сделав сечение с - с на участке KE из условия равновесия правой части, получаем 20 - 30 - Тк = 0. Откуда Тк = -10 кН * м.
Примем следующее правило знаков (рис. 2.4). Крутящий момент в сечении а - а считается положительным, когда внешний момент вращает отсеченную часть против часовой стрелки, если смотреть на отсеченную часть со стороны сечения. Если же внешний момент вращает отсеченную часть по часовой стрелке (при взгляде со стороны сечения), то крутящий момент в сечении будем считать отрицательным.
Построение эпюры крутящих моментов поясним на следующем примере (рис. 2.5): рассмотрим вал CD, опирающийся на подшипники B и A и находящийся в равновесии под действием приложенных к нему в сечениях E, K и L моментов. Сделав сечение а - а где-либо на участке DL и рассмотрев равновесие правой отсеченной части, убедимся, что Тк = 0. Если мы сделаем затем сечение b - b в любом месте участка LK, то из условия равновесия правой от сечения части получим Тк = 20 кН * м.
Момент считаем положительным в соответствии с принятым правилом знаков. Сделав сечение с - с на участке KE из условия равновесия правой части, получаем 20 - 30 - Тк = 0. Откуда Тк = -10 кН * м. 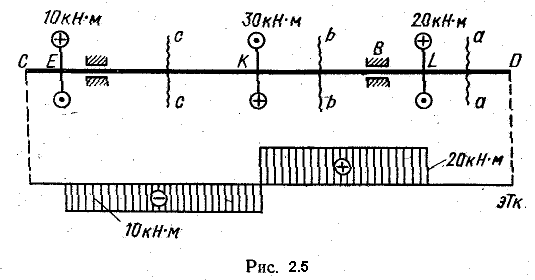 Получившаяся эпюра имеет форму двух прямоугольников. Важно заметить, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяюися на величину приложенного здесь внешнего момента.
Если заданы поперечные нагрузки, вызывающие кручение стержня (рис. 2.2), то предварительно вычисляют внешние скручивающие моменты, создаваемые этими силами. В случае, представленном на рис. 2.2, внешний скручивающий момент от силы F равен T = Fr. После определения внешних моментов определяют внутренние крутящие моменты и строят эпюры, как указано выше
Получившаяся эпюра имеет форму двух прямоугольников. Важно заметить, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяюися на величину приложенного здесь внешнего момента.
Если заданы поперечные нагрузки, вызывающие кручение стержня (рис. 2.2), то предварительно вычисляют внешние скручивающие моменты, создаваемые этими силами. В случае, представленном на рис. 2.2, внешний скручивающий момент от силы F равен T = Fr. После определения внешних моментов определяют внутренние крутящие моменты и строят эпюры, как указано выше