Ізокоста за своїм змістом і властивостями є аналогом бюджетної лінії споживача.

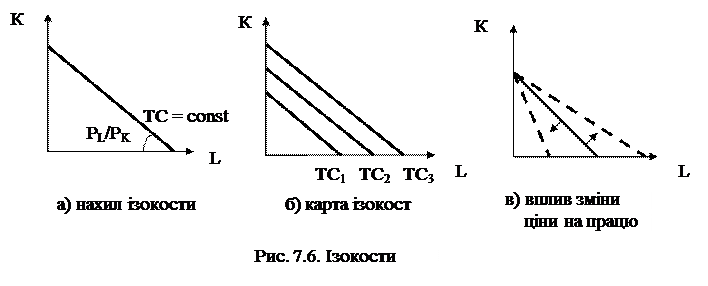
Властивості ізокости:

1. Всі точки ізокости відповідають однаковим сукупним витратам ресурсів.

2. Кут нахилу ізокости залежить від ціни ресурсу, його можна виразити наступним чином (див. рис. 7.6. а):

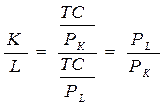
3. Чим далі від початку координат розміщена ізокоста, тим більший обсяг ресурсів використовується у виробництві.

4. Зміна ціни на працю чи капітал може змінити нахил ізокости. Наприклад, зростання ціни (зниження) ціни праці збільшує (зменшує) кут нахилу із зменшує ізокости.

Виробник намагається досягти стану рівноваги, тобто такої комбінації використовуваних ресурсів для виробництва означеного обсягу продукції, за якої величина витрат буде мінімальною.

Перед фірмою стоїть завдання знайти таку комбінацію праці і капіталу, яка за існуючих цін ресурсів забезпечила б мінімальні сукупні витрати на заданий фіксований обсяг виробництва.Для вирішення цього питання потрібно сумістити карту ізокост з фіксованою ізоквантою (рис. 7.7), остання показує технологічно ефективні комбінації для заданого рівня випуску.

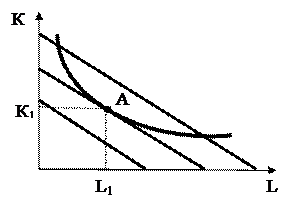Координати точки дотику (точка А) ізокости (однакових витрат) та ізокванти (заданий обсяг виробництва) показують, що обсяг продукції Q можна досягти комбінацією вхідних ресурсів К₁, L₁.

За допомогою функцій витрат можна вирішувати як прямі, так і зворотні задачі: визначення максимальних обсягів виробництва при заданих витратах. Для вирішення цього питання потрібно сумістити карту ізоквант з фіксованою ізокостою (рис. 7.8).

Умовою для визначення мінімальних витратах на заданий обсяг виробництва (як і максимальних обсягів виробництва при заданих витратах) є однаковий нахил ізокости та відповідної ізокости, що має спільну точку з ізокостою та найбільш віддалена від початку координат.

Нахил ізокванти визначається граничною нормою технологічного заміщення:

.

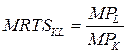Нахил ізокости – співвідношенням цін праці та капіталу: .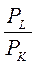

У точці дотику кут нахилу ізоквати збігається з кутом нахилу ізокости, тому умову рівноваги виробника, тобто такого його стану, в якому він не бажає замінювати співвідношення капіталу та праці, що задіяні у виробничому процесі, можна подати як рівність:

.

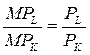Це рівняння має відображає принцип найменших витрат. Його суть у тому, що виробництво заданого обсягу продукції з мінімальними витратами вимагає, щоб ресурси, які одночасно використовуються, мали однакову величину граничного продукту на одиницю вартості ресурсу.

Питання для самоконтролю

1. Охарактеризуйте властивості виробничої функції з одним змінним ресурсом (аналітично, графічно).

2. У чому особливість виробничої функції з двома змінними факторами (аналітично, графічно).

3. Поясніть економічний зміст поняття “гранична норма технологічного заміщення ”.

4. Дайте визначення ізокости.

5. Розкрийте поняття рівноваги виробника, поясніть, як вона досягається.

6. Охарактеризуйте правило найменших витрат.

7. Охарактеризуйте залежність показників ТР_L, АР_l, МР_L на прикладі їх графіків.

8. Сформулюйте закон спадної віддачі.

9. Поясніть суть ефекту масштабу виробництва.

Рекомендована література: [1, 2, 3, 5, 7, 8, 9, 11].