
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Карта Карно (диаграмма Вейча).
|
|
Изучение принципов построения комбинационных устройств
Минимизация функций
Цель работы
Изучение способов задания функций алгебры логики (ФАЛ), законов алгебры логики, методов построения комбинационных устройств.
Основные понятия
Дискретные автоматы делят на два класса: комбинационные автоматы и автоматы с памятью.
В комбинационном автомате, называемом также автоматом без памяти или комбинационным устройством (схемой), каждый сигнал на выходе (логические 0 или 1) определяется лишь сигналами (логические 0 или 1), действующими в данный момент времени на входах автомата, и не зависит от сигналов, ранее действующих на этих входах. Комбинационный автомат не имеет памяти, он не хранит информации о своей прошлой работе.
В автоматах с памятью выходной сигнал определяется не только значениями сигналов на входах в данный момент времени, но и внутренним состоянием автомата. Внутреннее состояние автомата зависит от состояния его элементов памяти.
В данной лабораторной работе изучаются только комбинационные устройства (КУ) ‑ дискретные автоматы без внутренней памяти.
КУ можно рассматривать как функциональный преобразователь с большим числом входов и выходов, на каждом из которых имеется один разряд числа, принимающий одно из двух значений: 0 или 1.
Функциональная схема такого КУ приведена на рис.2.1.
На его вход подается входная величина Х в виде параллельного многоразрядного кода
Xm Xm-1 …X3 X2 X1 ,
где Х1 ‑ младший разряд числа,
Хm – старший разряд числа.
В течение короткого времени, меньшего длительности сигналов на входе, срабатывают отдельные элементы КУ, что приводит к появлению на выходе величины Y в виде параллельного многоразрядного кода
Ym Ym-1 …Y3 Y2 Y1 ,
где Y1 ‑ младший разряд числа (0 или 1),
Ym – старший разряд числа (0 или 1).
После прекращения действия входной величины Х исчезает выходная величина Y.
Зависимость числового кода Y выходной величины от числового кода Х входной величины определяется функцией алгебры логики (ФАЛ) или переключательной функцией (ПФ)
Y=F(X)=F(Xm Xm-1 …X3 X2 X1).
Всякое сложное КУ (рис. 2.1), имеющее много выходов, можно разбить на ряд простых КУ с одним выходом, каждый их которых соответствует одному разряду числового кода Y (рис. 2.2). В таком случае для описания функционирования сложного КУ вместо одной сложной ФАЛ F(X) можно использовать ряд простых ФАЛ F1, F2, F3, …, Fm, указывающих значение каждого разряда числового кода Y выходной величины в зависимости от числового кода Х входной величины, а именно:
Y1= F1(Xm Xm-1 …X3 X2 X1);
Y2= F2(Xm Xm-1 …X3 X2 X1);
………………………………
Ym= Fm(Xm Xm-1 …X3 X2 X1).
Функции алгебры логики (переключательные функции) F1, F2, F3, …, Fm могут принимать только одно из двух значений: 0 или 1 и называются булевыми функциями.
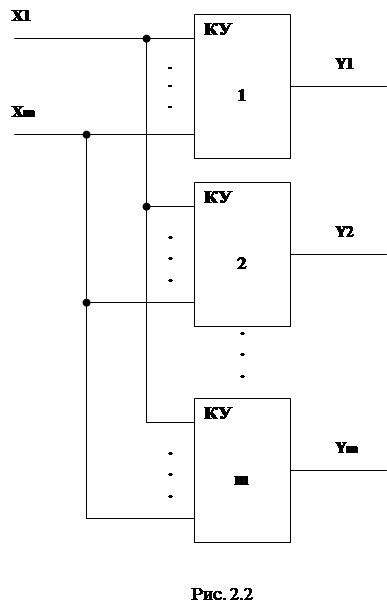 |

Числовые разряды Xm Xm-1 …X3 X2 X1 входной величины Х называются входными переменными или аргументамипереключательной функции F.
Конкретная комбинация Хk числовых значений всех аргументов носит название набора переменных, который представляет собою одно элементарное сообщение из заданного алфавита.
Реальные дискретные автоматы имеют конечное число входов, следовательно, число переменных соответствующих ФАЛ также конечно. Так как аргументы функции принимают только два значения, область определения любой ФАЛ также конечна. Общее число наборов двоичных аргументов, на которых определяется функция, будет
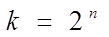 .
.
При каждом наборе переменных возможны два значения ФАЛ: 0 и 1. Поэтому в соответствие каждой ФАЛ можно поставить к-значное двоичное число. Следовательно, число функций алгебры логики
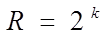 .
.
Число наборов одной переменной равно двум. Поэтому число ФАЛ одной переменной равно 4.
Число различных наборов значений двух переменных равно 4, а число различных возможных ФАЛ двух переменных составляет 16. В табл. 2.1 показаны функциональные схемы логических элементов, реализующих ФАЛ двух аргументов.
Любую функцию алгебры логики или просто логическую функцию можно задать одним из следующих способов:
- табличный способ (таблица истинности);
- числовая запись;
- аналитический способ (алгебраическая запись);
карта Карно (диаграмма Вейча).
Таблица 2.1
| Функция |  Символическое изображение Символическое изображение
| Функция | Символическое изображение |
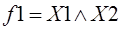 конъюнкция
конъюнкция
| 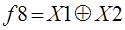 неравнозначность
(сумма по модулю 2)
неравнозначность
(сумма по модулю 2)
| ||
 дизъюнкция
дизъюнкция
| 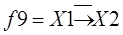 запрет Х1
запрет Х1
| ||
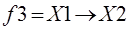 импликация
импликация
| 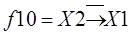 запрет Х2
запрет Х2
| ||
 импликация
импликация
| 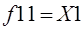 повторение Х1
повторение Х1
| ||
 штрих Шеффера
штрих Шеффера
| 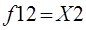 повторение Х2
повторение Х2
| ||
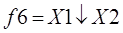 функция Вебба
(стрелка Пирса)
функция Вебба
(стрелка Пирса)
| 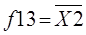 отрицание Х2
(инверсия Х2)
отрицание Х2
(инверсия Х2)
| ||
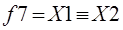 эквивалентность
(равнозначность)
эквивалентность
(равнозначность)
| 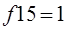 константа единицы
константа единицы
|
Табличный способ. Любая ФАЛ может быть задана с помощью таблицы, которую называют таблицей истинности, поскольку в математической логике логическая величина может принимать два значения, называемые «истина» и «ложь», а уж их цифровыми аналогами считаются соответственно 1 и 0.
Вид таблицы истинности приведен ниже.
| Номер набора | х1 | х2 | ... | хN | f |
| ... | ... | ... | ... | ... | |
| ... | ... | ... | ... | ... | |
| ... | ... | ... | ... | ... | ... |
| ... | ... | ... | ... | ... | ... |
В левых (х1,...хN) столбцах перечисляются все возможные наборы аргументов, а в самом правом столбце - значения функции для соответствующих входных наборов. Самый левый столбец таблицы вообще-то не нужен и введен только для удобства работы с таблицей, главным образом для того, чтобы систематизировать построение таблицы, когда число наборов велико и возникает опасность ошибочно записать некоторый набор более одного раза или опустить какой-то из наборов.
Можно предложить следующее правило построения таблицы. По известному числу двоичных элементов N (разрядности входного слова) определяют число различных наборов (при n переменных таблица содержит 2n строк). Нумеруют наборы целыми числами начиная с 0. Далее каждый номер набора представляют в виде двоичного числа разрядности N. Этот набор записывают в соответствующей строке таблицы истинности. Повторив указанное действие для каждого набора, получают подготовленную таблицу входных наборов, а уже затем, согласно конкретной функциональной зависимости описываемой функции, заполняют правый столбец таблицы истинности.
Пример. В таблице 2.2 задана ФАЛ трех переменных f(x1, x2, x3). При трех переменных можно образовать восемь наборов, каждый из которых представляет собой трехразрядное двоичное число.
Таблица 2.2
| номер набора | X1 | X2 | X3 | f |
Числовой способ. При задании функции каждому набору переменных ставят в соответствие определенное число в двоичной системе счисления и присваивают соответствующий номер. Функцию задают в виде десятичных номеров тех наборов, на которых она принимает единичное значение. Переменным х1, х2,...., хn приписываются соответствующие веса и переменные записываются в порядке уменьшения веса.
Пример. Для трех переменных функция, запишется:
f = {0, 3, 4, 7}x1x2x3;
для четырех переменных:
g = {2, 3, 4, 5, 6, 10, 11, 12, 13}x1x2x3x4.
Аналитический способ. При аналитическом (формульном) способе задания функцию задают в виде алгебраического выражения, показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции.
Аналитические выражения для функций f(x1, x2, x3) и g(x1, x2, x3, x4) имеют вид:
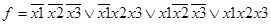
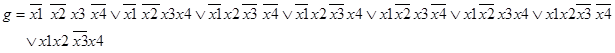 При аналитическом способе задания переключательной функции используется суперпозиция - подстановка функции вместо аргумента. Используя суперпозицию, можно получить любую сколь угодно сложную функцию. В аналитическом выражении порядок выполнения действий определяется старшинством функций (операций), а если он не подходит, используют круглые скобки. Наивысший приоритет (старшинство) имеет функция НЕ, затем И, а наименьший - функция ИЛИ.
При аналитическом способе задания переключательной функции используется суперпозиция - подстановка функции вместо аргумента. Используя суперпозицию, можно получить любую сколь угодно сложную функцию. В аналитическом выражении порядок выполнения действий определяется старшинством функций (операций), а если он не подходит, используют круглые скобки. Наивысший приоритет (старшинство) имеет функция НЕ, затем И, а наименьший - функция ИЛИ.
Пример. Пусть надо записать функцию
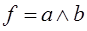 ,
,
где
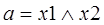 ,
,
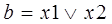 ,
,
тогда
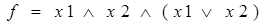 .
.
Аналитический способ позволяет задать сложную функцию значительно компактнее, чем табличный. Однако, особенно на первом этапе, табличный метод удобнее и нагляднее
Карта Карно. Функцию задают в виде координатной карты состояний, которую называют картой Карно. Карты представляют прямоугольные таблицы, разделенные горизонтальными и вертикальными линиями на клетки. Общее число клеток соответствует числу наборов функции. Все переменные разбивают на две группы. Одна группа определяет выбор строки, другая - выбор столбца. На пересечении строки и столбца находится клетка, в которую записывают значение функции при соответствующем наборе переменных. Разделение переменных на группы осуществляется так, чтобы в соседних клетках наборы различались только значением одной переменной. В клетках, соответствующих единичным наборам ФАЛ проставляются единицы, клетки, соответствующие нулевым наборам, обычно не отмечаются, т.е. нулевым наборам соответствуют пустые клетки карты.
Карты Карно для функции трех переменных f = {0, 3, 4, 7}x1x2x3 и функции четырех переменных g = {2, 3, 4, 5, 6, 10, 11, 12, 13}x1x2x3x4 приведены на рис.2.3а и рис.2.3б.
a)
| х1х2 х3 | ||||
б)
| х1х2 х3x4 | ||||
Рис. 2.3. Задание функции алгебры логики с помощью карты Карно
Наибольший практический интерес представляют для нас три функции.
Логическое отрицание НЕ. Эта функция является функцией одной переменной и определяет ее инверсию. Она истинна тогда, когда ложна переменная, и ложна, когда переменная истинна. Значения функции задаются таблицей истинности. Таблица истинности имеет следующий вид:
| Номер набора | X | 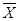
|
При использовании аналитической (формульной) записи функция логического отрицания значения переменной (далее просто отрицания или НЕ) изображается чертой над именем переменной.
Запись " 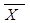 " читается как " не X".
" читается как " не X".
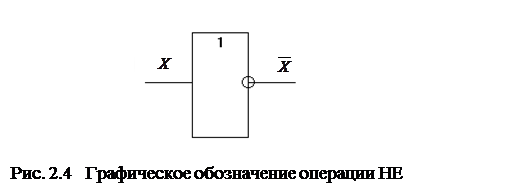 Функция НЕ графически обозначается кружком на входе или выходе логического символа.
Функция НЕ графически обозначается кружком на входе или выходе логического символа.
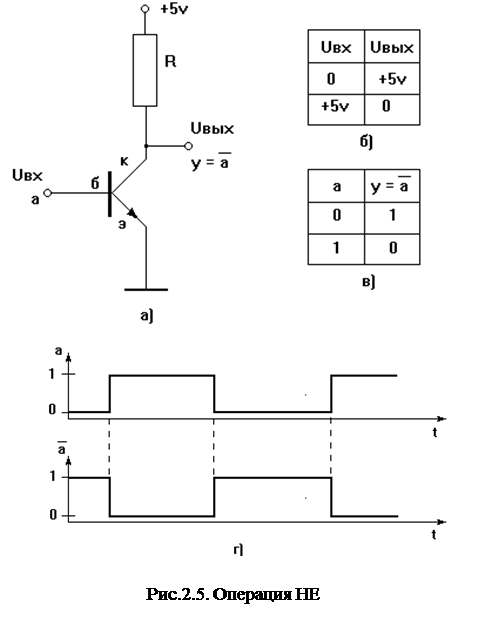
Для физической (аппаратной) реализации отрицания в простейшем случае используется элемент " инвертор". Электрическая схема инвертора, уровни напряжений на ее входе и выходе приведены на рис.2.5. Там же приведена и таблица истинности функции.
Транзистор в этой схеме работает в режиме ключа - он или закрыт, и тогда через него не протекает ток, а его сопротивление можно считать равным бесконечности, или открыт, и при этом через него протекает максимально возможный ток, а его сопротивление можно считать равным нулю.
Состояние напряжений на входе и выходе инвертора можно изобразить графически в виде так называемой временной диаграммы, на которой по оси абсцисс откладывается время, а на оси ординат напряжение (или условный логический уровень 0 или 1) для входа и выхода. В последнем случае можно говорить о логической временной диаграмме. Логическая временная диаграмма инвертора приведена на рис. 2.5(г).
 |
Логическое умножение. Эта функция является функцией двух переменных и истинна тогда и только тогда, когда одновременно истинны обе входные переменные. Эта функция имеет несколько названий. Кроме названия " логическое умножение", она называется также функцией конъюнкции или функцией И. При использовании аналитической (формульной) записи функция логического умножения (конъюнкции, И) изображается символом &, знаком  или точкой (как это делается при изображении операции умножения в математике). Запись "
или точкой (как это делается при изображении операции умножения в математике). Запись " 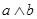 " читается " a и b".
" читается " a и b".
Графическое обозначение функции приведено на рис.2.6.
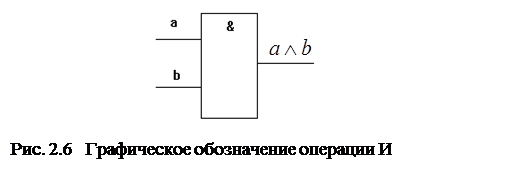 |
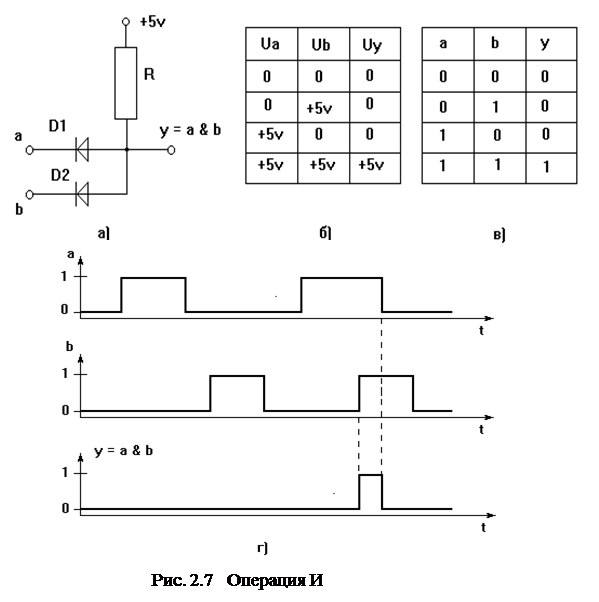 Таблица истинности функции, простейшая электрическая схема, реализующая конъюнкцию двух переменных, а также таблица напряжений входов и выхода схемы и логические временные диаграммы схемы приведены на рис.2.7.
Таблица истинности функции, простейшая электрическая схема, реализующая конъюнкцию двух переменных, а также таблица напряжений входов и выхода схемы и логические временные диаграммы схемы приведены на рис.2.7.
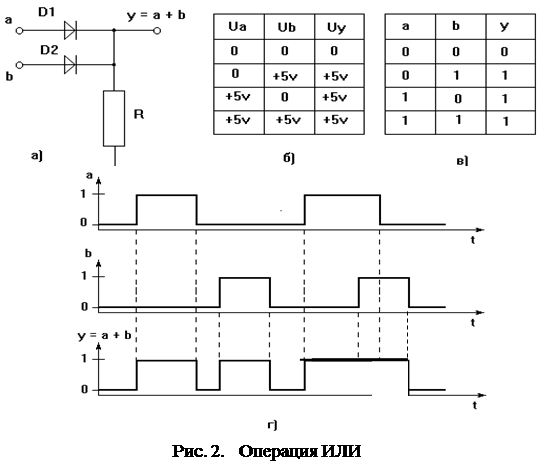
Логическое сложение. Эта функция является функцией двух переменных и истинна тогда, когда истинна хотя бы одна входная переменная. Функция имеет несколько названий - " логическое сложение", функция дизъюнкции или функция ИЛИ. При использовании аналитической (формульной) записи функция логического сложения (дизъюнкции, ИЛИ) изображается символом " Ú " или знаком объединения. Запись " а Ú в" читается " а или в".
Графическое обозначение функции приведено на рис.2.8.
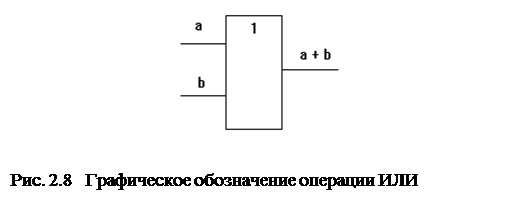 |
Таблица истинности функции, простейшая электрическая схема, реализующая дизъюнкцию двух переменных, а также таблица напряжений входов и выхода схемы и логические временные диаграммы схемы приведены на рис.2. 9.
Три рассмотренные функции позволяют реализовать любую логическую функцию, сколь бы сложна она ни была. Однако удобнее проиллюстрировать это можно при использовании аналитического, а не табличного способа.
Основные законы алгебры логики. Решение вопросов анализа и синтеза схем дискретных устройствжелезнодорожной автоматики, телемеханики и связи связано с преобразованием выражений, которые содержат ФАЛ основного базиса. Запись, содержащая двоичные переменные, соединенные знаками логического сложения, умножения и инверсии, называют логическим выражением. Такое выражение однозначно определяет комбинационное устройство, построенное на элементах И, ИЛИ, НЕ.
Основные законы булевой алгебры, позволяющие производить различные тожденственные преобразования формул булевой алгебры, включают:
1) Закон двойного отрицания
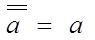
2) Переместительный закон (закон коммутативности)
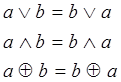
3) Сочетательный закон (закон ассоциативности)
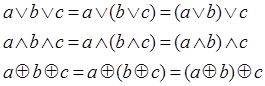
4) Распределительный закон (закон дистрибутивности)
а  (в Ú с) = а
(в Ú с) = а  в Ú a
в Ú a  с
с
а Ú в  c = (a Ú в)
c = (a Ú в)  (a Ú c)
(a Ú c)
При доказательстве правильности тех или иных законов обычно используют таблицы истинности. Проиллюстрируем этот прием для доказательства правильности последнего закона.
Поскольку функция имеет 3 входа, число возможных входных наборов равно 8 (см. таблицу на следующей странице).
Значения функции в столбце " а Ú в  с" получается при использовании значений столбцов " а" и " в
с" получается при использовании значений столбцов " а" и " в  с", а в столбце " (а Ú в)
с", а в столбце " (а Ú в)  (а Ú c)" - при использовании столбцов " а Ú в" и " а Ú с". Сравнение значений двух правых столбцов таблицы доказывает правильность второй записи распределительного закона.
(а Ú c)" - при использовании столбцов " а Ú в" и " а Ú с". Сравнение значений двух правых столбцов таблицы доказывает правильность второй записи распределительного закона.
| Номер набора | а | в | с | в  с с
| а Ú в | а Ú с | аÚ в  c c
| (а Ú в)  (а Ú с) (а Ú с)
|
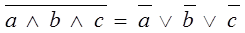 5) Правило де-Моргана
5) Правило де-Моргана
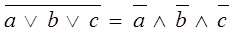 |
6). Правила операций с константами 0 и 1
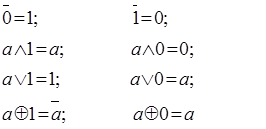
7) Правила операций с переменной и ее инверсией

8) Закон повторения
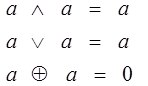
Следствие закона повторения - правило приведения подобных членов в выражении:
a  a
a  ...
...  a = a
a = a
a Ú a Ú... Ú a = a
9) Закон поглощения
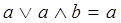
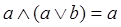
Для доказательства правильности закона используем аналитический метод и уже известные законы.
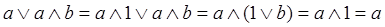
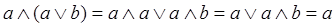
10) Закон склеивания
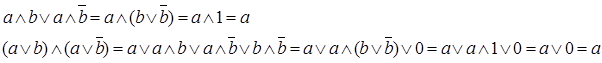 Примеры использования рассмотренных законов для упрощения логических выражений.
Примеры использования рассмотренных законов для упрощения логических выражений.