Общие теоремы прямого метода Ляпунова.

При исследовании систем импульсного и релейного регулирования возникают вопросы об определении устойчивости стационарного состояния движения или равновесия, когда в возмущенном движении известны состояния системы в дискретные равностоящие друг от друга моменты времени. Эти вопросы тесно связаны с изучением свойств решений систем разностных уравнений, и поэтому имеет смысл рассмотреть их в общем виде^[1].

Рассмотрим систему нелинейных разностных уравнений, заданных в нормальной форме

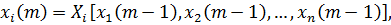(1.1)

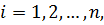
которые устанавливают связь между переменными 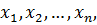для двух последовательных, равноотстоящих друг друга значений независимого переменного 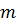. Не нарушая общности, будем считать, что переменно 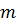принимает только целочисленное значения 0, 1, 2 … Независимую переменную 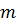, как и прежде, будем называть дискретным временем.

Правые части уравнений (1.1) суть однозначные, непрерывные функции переменных 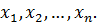При этих условиях всякая система значений переменных 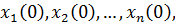принимаемая за начальные условия при 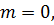определяет единственное решение Х уравнений (1.1), которое при 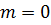удовлетворяет начальным условиям. Это решение будет непрерывно зависеть от начальных условий.

Будем считать, что существует область

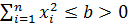(1.2)

изменения переменных 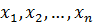внутри которой правые части (1.1) непрерывны и не обращаются одновременно в нуль, кроме значений переменных

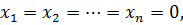(1.3)

при которых

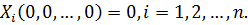(1.4)

Геометрически переменные 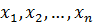можно трактовать как координаты n-мерного фазового пространства, а решение системы разностных уравнений (1.1)- как движение изображающей точки. Тогда систему уравнений (1.1) можно назвать дискретной системой^[2]. Дискретная динамическая система осуществляет точечное преобразование фазового пространства. Тогда 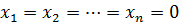являются неподвижной, или инвариантной, точкой данного преобразования.

Равенства (1.3) определяют тривиальное решение уравнений (1.1). В соответствии с терминологией Ляпунова^[3] 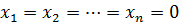будем называть невозмущенным движением системы, а уравнения (1.1)- уравнениями возмущенного движения, а их решения – возмущенными движениями системы.

Правые части уравнений (1.1) не зависят явно от дискретного времени М, поэтому их решение определяет устойчивость установившихся невозмущенных движений. Однако, как будет показано ниже, к анализу решений такого типа разностных уравнений будет сведена задача об устойчивости периодических режимов колебаний релейных систем регулирования.

Для дискретных систем можно сформулировать определение устойчивости по Ляпунову.

Если для всякого произвольно задаваемого числа 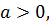как бы мало оно ни было, можно выбрать положительное число 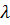так, что для всех возмущенных движений Х для которых в начальный момент времени 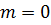выполняется неравенства

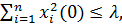(1.5)

будут иметь место неравенства

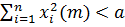(1.6)

для любого значения 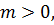то невозмущенное движение (1.3) устойчиво^[4]. В противном случае неустойчиво и устойчиво асимптотически, если дополнительно имеют место предельные равенства

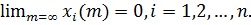(1.7)

Решение вопроса об устойчивости дискретных систем дается естественным распространением теорем прямого метода Ляпунова на рассматриваемый случай. Пусть существует вещественная функция 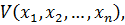относительно которой будем предполагать, что существует достаточно малая область

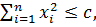(1.8)

внутри которой она однозначна, непрерывна и обращается в нуль, когда все координаты Х суть нули. Будем дополнительно считать, что функция 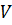является знакоопределенной положительной (отрицательной), если для всех значений координат удовлетворяющих неравенству (1.8), кроме 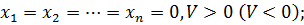знакопостоянной положительной (отрицательной), если при указанных выше условиях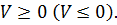

Если функция 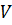не является знакоопределенной или знакопостоянной, то в любой сколь угодно малой окрестности точки 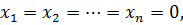то функция 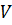может принимать как положительные, так и отрицательные значения. Такую функцию будем называть знакопеременной.

Введем обозначения

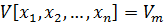(1.9)

и будем говорить, что первая разность 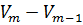функций 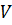взята в силу уравнений (1.1), если в ней переменные 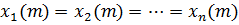выражены через 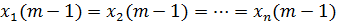посредством указанных уравнений.

Первая теорема об устойчивости. Если разностные уравнения (1.1) возмущенного движения таковы, что можно найти знакоопределенную функцию 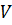первая разность которой в силу этих уравнений была бы знакопостоянной функцией противоположного знака с 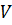или тождественно равна нулю, то невозмущенное движение устойчиво.

Эта теорема доказывается почти дословным повторением соответствующей теоремы Ляпунова. Пусть 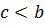и 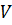есть определенно положительная функция, а первая разность ее, взята в силу уравнений (1.1), удовлетворяет уравнению

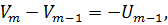(1.10)

где U - знакопостоянная положительная функция.

Отсюда суммирование получим

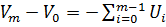(1.11)

и, учитывая, что 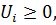будем иметь

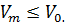(1, 12)

Пусть, далее, a есть некоторое произвольно малое положительное число (которое во всяком случае будем полагать меньше c); пусть l есть точная низшая граница функции V на сфере a

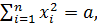(1.13)

т.е. для всех точек сферы a имеет место неравенство

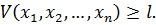(1.14)

Число l отлично от нуля и положительно, так как 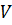представляет собой определенно положительную функцию. С другой стороны, для l найдется такое 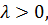что для значений переменных удовлетворяющих условию

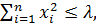(1.15)

значение функции 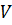будут удовлетворять неравенству

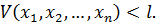(1.16)

Такое значение необходимо существует в силу свойств функции 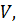оговоренных выше. Если при 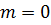начальные значения координат 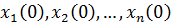выбраны таким образом, что они удовлетворяют неравенству (1.15), то в соответствии с формулами (1.9), (1.12) и (1.16) для любого момента дискретного времени будут иметь место неравенства

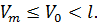(1.17)

Ввиду того, что в процессе движения 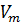не достигает значения l то в силу неравенств (1.13) и (1.14) изображающая точка никогда не достигает сферы a, т.е. для любого момента времени 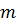координаты 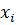удовлетворяют неравенству (1.6).

Вторая теорема об устойчивости. Если разностные уравнения (1.1) возмущенного движения таковы, что можно найти знакоопределенную функцию 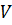, первая разность которой в силу этих уравнений была бы знакоопределенной функцией противоположного с 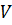знака, то невозмущенное движение устойчиво асимптотически.

В данном случае, очевидно, выполняется условия первой теоремы. Поэтому невозмущенное движение устойчиво. Покажем, что здесь имеют место предельные равенства (1.7). Пусть функция 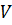является определенно положительной. Тогда в уравнении (1.10) 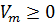и 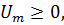причем знак равенства имеет место при 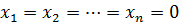. Из (1.10) следует, что с изменением времени m функция 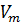образует монотонно убывающую последовательность

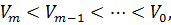(1.18)

ограниченную снизу нулем. Следовательно, эта последовательность стремиться к пределу при неограниченно возрастающем 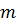. Этот предел равен нулю, и в силу определенной положительности функции 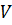координаты 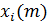в пределе также равны нулю.

Это положение доказывается от противного. Пусть указанный предел равен 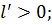тогда существует такая окрестность, ограниченная сферой 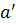в которую не может проникнуть изображающая точка с координатами 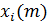при любом m. Вследствие этого определенно положительная функция 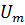для любого m будет больше некоторого, не равного нулю положительного числа 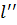. Но тогда из формулы (1.11) легко получить неравенство

, (1.19)

по которому функция 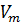наверняка становится отрицательной, что невозможно.

Имеют место две теоремы о неустойчивости.

Первая теорема о неустойчивости. Если разностные уравнения (1.1) возмущенного движения таковы, что можно найти функцию V которая обладала бы в силу этих уравнений знакоопределенной первой разностью и была бы такова, что при надлежащем выборе величин 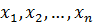, численно сколь угодно малых ее можно было бы сделать величиной одинакового знака с ее первой разностью, то невозмущенное движение неустойчиво.

Вторая теорема о неустойчивости. Если разностные (1.11) возмущенного движения таковы, что можно найти функцию V первая разность которой в силу этих уравнений приводилось бы к виду

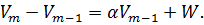(1.20)

где 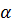- положительная постоянная, а W или тождественно равна нулю или представляет собой некоторую знакопостоянную функцию и при этом найденная функция V такова, что надлежащим выбором величин 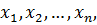численно сколь угодно малых, ее можно сделать величиной одинакового знака с W то невозмущенное движение неустойчиво.

В частности, условия теорем о неустойчивости наверняка будут выполнятся, если функция V будет знакопостоянной или знакоопределенной функцией одного знака с первой разностью (первая теорем) или с функцией В (вторая теорема).

Доказательство этих теорем легко провести, следуя соответствующим рассуждениям Ляпунова с теми упрощениями и изменениями, которые теперь ясны из данных выше доказательств теорем об устойчивости, поэтому мы их здесь в аналитическим виде приводить не будем.

Приведенные выше теоремы Ляпунова об устойчивости движения допускают очень наглядную геометрическую интерпретацию^[5]. Пусть V есть знакоопределенная положительная функция. Рассмотрим в фазовом пространстве однопараметрическое семейство поверхностей

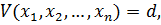(1.21)

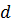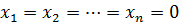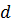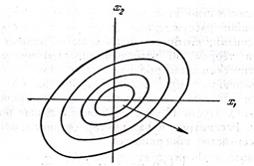
где параметр - положительное число. Будем называть их поверхностями равного уровня. Очевидно, V (0) вырождается в точку. Существует такая достаточно малая окрестность (1.8) около нулевой точки , в которой поверхности уровня будут замкнутыми и охватывающими нулевую точку. При изменении параметра от нуля до некоторого достаточно малого значения получим однопараметрическое семейство замкнутых, не пересекающихся между собой поверхностей разного уровня, охватывающих нулевую точку и стягивающихся в эту точку при 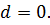На рис. 1.1 это поверхности представлены в виде кривых равного уровня для случая двухмерного фазового пространства – фазовой плоскости.

Каждая поверхность (1.21) охватывает все поверхности семейства, соответствующие более низкому уровню параметра 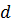. Величины 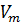вычисленные для текущих значений 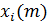координат изображающей точки, всегда совпадают с определенными значениями параметра 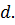Это означает, что в данный момент времени изображающая точка с координатами 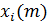попадает на поверхность указанного уровня. Таким образом, в дискретном движении изображающая точка перескакивает с одной поверхности равного уровня на другую, причем, если первая разность 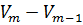представляет собой знакоопределенную функцию противоположного с V знака^[6], то изображающая точка всегда перескакивает с поверхности данного уровня на поверхность более низкого уровня и поэтому асимптотически приближается к нулевой точке. Если первая разность 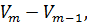взята в силу уравнений (1.1), тождественно равна нулю или является знакопостоянной функцией противоположного с V знака, то изображающая точка при своем движении может «застрять» на поверхности определенного уровня и тогда она наверняка не сможет неограниченно приближается к нулевой точке.

а)

б)

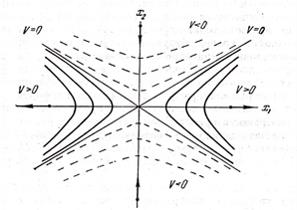
Рис. 1.1, Кривые равного уровня для знакоопределенной и знакопеременной функций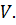

Если теперь функция V знакопеременная, то поверхности уровня (1.21) не будут замкнутыми. Параметр 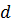в этом случае может принимать положительные и отрицательные значения, так что в окрестности нулевой точки будем иметь области 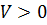и 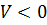причем эти области разделяются поверхностью 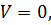которая проходит через нулевую точку 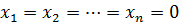. В области 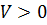поверхности (1.21) равного уровня не пересекаются в силу однозначности функции V и удаляются от нулевой точки с увеличением положительного параметра 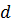в области 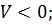с ростом отрицательного параметра 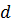поверхности равного уровня, наоборот, как бы приближаются к нулевой точке и к разделяющей поверхности 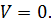На рис. 1.1, б представлена подобная ситуация для фазовой плоскости. В любой сколь угодно малой окрестности нулевой точки существует област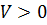и и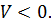

Пусть первая разность 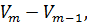вычислена в силу разностных уравнений (1.1), -определенно положительная функция. Тогда, если движение начинается из точки области 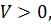находящая точка в процессе дискретного движения будет перескакивать с поверхностей низшего уровня на поверхности более высокого уровня. Изображающая точка, не покидая области 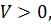обязательно выйдет за пределы любой наперед задаваемой области (1.6), поэтому невозмущенное движение будет неустойчивым. Заметим, что для доказательства неустойчивости невозмущенного движения достаточно найти хотя бы одну фазовую траекторию, которая выходит за пределы области (1.6).

В предыдущих рассуждениях не был в полной мере использован тот факт, что первая разность является определенно положительной функцией. Для доказательства достаточно только знать, что в любой близости нулевой точки существует область 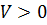и что первая разность 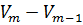взята в силу уравнений (1.1), является положительной в этой области.

Такое обозначение теорем Ляпунова о неустойчивости было дано Н.Г. Четаевым.

Общие теоремы об устойчивости невозмущенного движения дискретных динамических систем являются естественным обобщением соответствующих теорем Ляпунова. Функцию V, обладающую свойствами, которые оговорены в одной из четырех теорем, называют обычно функцией Ляпунова.

Приложение Общих теорем к исследованию устойчивости линейных дискретных систем требует своеобразного подхода, причем применение методов матричного исчисления позволяют получить решение такой задачи довольно простыми средствами.