
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Гомогенный реактор с линейной температурной обратной связью.
|
|
Рассмотрим точечную модель гомогенного реактора в предположении, что реактивность зависит от температуры горючего по линейному закону. Уравнения динамики запишутся в виде:
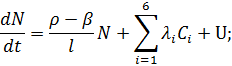
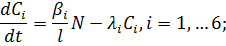
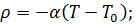 (2.3.1)
(2.3.1)
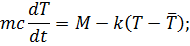
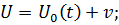
где 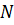 - мощность реактора;
- мощность реактора; 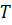 - температура делящегося вещества;
- температура делящегося вещества; 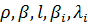 - постоянные;
- постоянные; 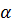 - температурный коэффициент реактивности;
- температурный коэффициент реактивности; 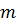 и
и 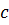 - масса и удельная теплоемкость горючего,
- масса и удельная теплоемкость горючего, 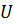 - управление. Постоянные
- управление. Постоянные 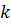 и
и 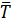 имеют различное содержание в зависимости от конкретного механизма отвода тепла. Так, если теплоотвод осуществляется циркуляцией горючего, то k=Gc, где G - массовый расход горючего, а
имеют различное содержание в зависимости от конкретного механизма отвода тепла. Так, если теплоотвод осуществляется циркуляцией горючего, то k=Gc, где G - массовый расход горючего, а 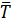 -постоянная температура горючего на входе в активную зону. Если же тепло отводится охлаждением через поверхность, то k- коэффициент теплопередачи от горючего с температурой Т к охлаждающей среде с температурой
-постоянная температура горючего на входе в активную зону. Если же тепло отводится охлаждением через поверхность, то k- коэффициент теплопередачи от горючего с температурой Т к охлаждающей среде с температурой 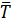 . В системе (2.3.1) и всюду ниже индекс «0» указывает на значение переменной в стационарной системе.
. В системе (2.3.1) и всюду ниже индекс «0» указывает на значение переменной в стационарной системе.
Система (2.3.1) допускает два разных состояния равновесия:
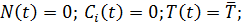
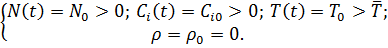
Первое состояние равновесия характеризует погашеный реактор. Второе состояние равновесия описывает стационарный режим при отличном от нуля уровне мощности.
Рассмотрим задачу устойчивости системы (2.3.1) в отклонениях при
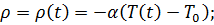
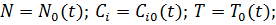 (2.3.2)
(2.3.2)
Перейдем к новым переменным
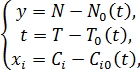
Учитывая уравнения (2.3.2) получим
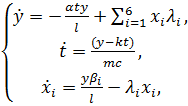 (2.3.3)
(2.3.3)
Применим функцию Ляпунова
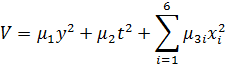
Производная от функции Ляпунова равна
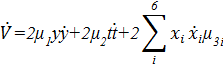
Подставляя соответствующие значения получим
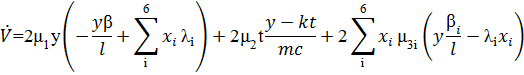
Раскрыв скобки получаем
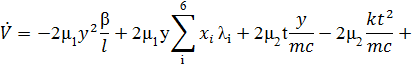
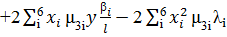 (2.3.4)
(2.3.4)
Выпишем матрицу коэффициентов квадратичной формы (2.3.4)


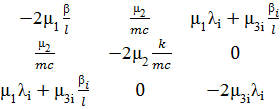
Применяя критерии асимптотической устойчивости линейного приближения, получим
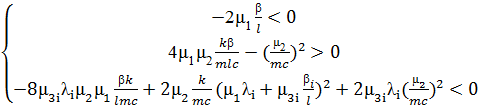 (2.3.5)
(2.3.5)
При условиях (2.3.5) система уравнений (2.3.3) асимптотически устойчива, а значит и исходная система (2.3.1) тоже асимптотически устойчива.
Было проведено численное моделирование системы (2.3.1) при следующих численных значениях (Приложение 1).
Заключение
Список литературы
* Эти возмущения всегда существуют в реальной установке; они носят, как правило, случайный характер и не поддаются точным количественным оценкам.
[1] Поставленный вопрос рассматривался автором с точки зрения построения функций Ляпунова в 1953 г. В 1919 г. Е. Коттон применял к анализу решений нелинейных разностных уравнений теорию характеристических чисел Ляпунова.
[2] Такое наименование находится в соответствии с терминологией принятой в качественной теории дифференциальных уравнений.
[3] С вопросами теории устойчивости движения по Ляпунову читатель может познакомиться по монографиям А.М. Ляпунова, Н.Г. Чатаева и И.Г. Малкина.
[4] Иногда говорят обыкновенно устойчиво или просто устойчиво.
[5] См. цитированную выше книгу И.Г. Малкина.
[6] То есть в данном случае определенно отрицательную функцию.
1. Библиографический указатель работ по устойчивости стационарных режимов ядерных энергетических установок (1954 – 1973 гг.) АИНФ 233. М., ЦНИИатомицформ, 1974. (Сост.: С.Л. Горяченко, В.Д. Гориченко).
2. Бернштейн С.И., Соловьев М.М. Автоколебания в системе регулирования мощности реактора с двумя управляющими органами. – В ки.: Управление ядерными энергетическими установками. Вып. 2. М., Атомиздат, 1967, с. 72 – 85.
3. Kando H., Iwazumi T., Hattory Y. Consideration of eigenvalue sensitivity for reactor system. – «J. Nuel. Sci. and Techn.», 1971, v. 8, № 7, p. 363 – 370.
4. Raju G. V. S., Josselson R. Stability of reactor control system in coutied core reactors. – «IEEE Trans. Nucl. Sci.», 1971, v. 18, № 1 (Part 1), p. 388-394.
5. Шульц М. Регулирование энергетических ядерных реакторов. Пер. с англ. Под ред. Д.И. Воскобойника. М., Изд-во иностр. лит., 1957.
6.Мистенко Ф.М., Моторов Б.И. Нестационарные режимы судовых ядерных паропроизводящих установок. Л., «Судостроение», 1970.
7.Основы автоматического управления ядерными космическими энергетическими установками. М., «Машиностроение», 1974, Авт.: В.В. Бугровский, Н.А. Винцевич, И.М. Вышнепольский и др.
8. Анапольский, Л.Ю. Метод сравнения в динамике дискретных систем / Л.Ю. Анапольский; ред. В.М. Матросов, Л.Ю. Анапольский // Вектор-функции Ляпунова и их построение. – Новосибирск: Наука, 1980.- С. 92-128.
9. Андреев, А.С. О моделировании цифрового регулятора на основе прямого метода Ляпунова / А.С. Андреев, Е.А. Кудашова, О.А. Перегудова // Научно-технический вестник Поволжья. – 2013. - №6. – С. 113-115.
10. Андреев, А.С. О моделировании цифрового регулятора на основе прямого метода Ляпунова / А.С. Андреев, Е.А. Кудашова, О.А. Перегудова // Научно-технический вестник Поволжья №6 2013. Казань: Научно-технический вестник Поволжья, 2013 – с. 113-115.
11. Беллман, Р. Дифференциально-разностные уравнения / Р. Беллман, К. Кук. – М.: Мир, 1967. – 548 с.
12. Богданов А.Ю. Устойчивость неавтономных дискретных систем типа Лотки – Вольтерра / А.Ю. Богданов, Е.А. Кудашова // Ученые записки УлГУ. Сер. Математика и информационные технологии. Вып. 1(18) – Ульяновск: УлГУ, 2007. – С. 182-188.
13. Богданов А.Ю. Развитие прямого метода Ляпунова и равномерная асимптотическая устойчивость решений дискретных с изменяющейся структурой / А.Ю. Богданов, Е.А. Кудашова // Обозрение прикладной и промышленной математики. Москва: ТВП. - 2009. – Том 16 – Вып. 2. – С. 294-295.
14. Бромберг, П.В. Матричные методы в теории релейного и импульсного управления / П.В. Бромберг. – М.: Наука, 1967. – 324 с.
15. Видаль, П. Нелинейные импульсные системы / П. Видаль. – М.: Энергия, 1974. – 336 с.
16. Гайшун, И.В. Дискретные уравнения с изменяющейся структурой и устойчивость их решений / И.В. Гайшун // Дифференциальные уравнения. – 1997. – Т. 33, №12. – С. 1607-1614.
17. Гайшун, И.В. Устойчивость дискретных процессов Вольтерра с Убывающим последействием / И.В. Гайшун // Автоматика и телемеханика. – 1997. – №6. – С. 118-124.
18. Гайшун, И.В. Управляемость систем, описываемых линейными дискретными уравнениями Вольтерра / И.В. Гайшун, М.П. Дымков // Автоматика и телемеханика. – 2000. – №7. – С. 88-100.
19. Гайшун, И.В. Системы с дискретным временем / И.В. Гайшун. – М.: Минск, 2011.
20. Гайшун, И.В. Системы с дискретным временем / И.В. Гайшун. – Минск: Институт математики НАН Беларуси, 201.
21. Гелиг, А.Х. Стабилизация нестационарных импульсных систем / А.
Х. Гелиг, И.Е. Зубер // Автоматика и телемеханика. – 2004. – №5. – С. 29-37.
22. Колмановский, В.Б. О применении второго метода Ляпунова к разростным уравнениям Вольтерра / В.Б. Колмановский // Автоматика и телемеханика. – 1995, №11. – С. 50-64.
23. Кудашова Е.А. Метод векторных функций Ляпунова в задаче об асимптотической устойчивости разностных систем / О.А. Перегудова, Е.А. Кудашова // Научно-технический вестник Поволжья, 2015. – с. 118-121.
24. Кудашова Е.А. Об асимптотическом поведении решений неавтономной нелинейной системы второго порядка / Е.А. Кудашова //Труды Симбирской молодежной научной школы по аналитической динамике, устойчивости и управлению движениями и процессами, 8-12 июня 2009 г., г. Ульяновск. – Ульяновск: УлГУ, 2009. С. 67-68.
25. Кудашова Е.А. Прямой метод Ляпунова в задаче об устойчивости неавтономных дискретных систем типа Лотки-Вольтерра / Е.А. Кудашова // Труды Х международной Чатаевской конференции «Аналитическая механика, устойчивость и управление», - Казань: КНИТУ КАИ. – с. 316-322.
26. Леонов, Г.А. Проблема Броккета для линейных дискретных систем управления /Г.А. Леонов // Автоматика и телемеханика. – 2002. – №5. – С. 92-96.
27. Маликов, А.И. Вектор функции Ляпунова в анализе свойств систем со структурными изменениями / А.И. Маликов, В.М. Матросов // Дифференциальные уравнения. – 1998. – №2. – С. 47-54. 530 с.
28. Перегудова, О. А. Метод сравнения в задачах устойчивости и управления движениям механических систем / О.А. Перегудова. – Ульяновск; Издательство УлГУ, 2009. – 253 с.
29. Самарский, А.А. Устойчивость разностных систем / А. А. Самарский, А.В. Гулин. – М.: Наука, 1973. – 397 с.
30. Фурасов, В.Д. Устойчивость и стабилизация дискретных процессов / В.Д. Фурасов. – М.: Наука, 1982. – 192 с.
31. Цыпкин, Я.З. Теория линейных импульсных систем / Я.З. Цыпкин. – М.: Наука, 1963. – 968 с.
32. Юревич, Е.И. Основы робототехники / Е.И. Юревич. – 2-е изд. – СПб.: БХВ-Петербург, 2005. – 416 с.
33. Юревич, Е.И. Теория автоматического управления / Е.И. Юревич. – 3-е изд. – СПб.: БХВ-Петербург, 2007. – 560 с.