
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие о теории графов
|
|
Содержание
3.1. Понятие о теории графов
3.2. Анализ размерных связей деталей с использованием теории графов
3.3. Выбор технологических баз
3.4. Синтез технологического маршрута
Основным способом автоматизации проектирования процессов механической обработки в условиях единичного производства является автоматизация по методу анализа размерных связей.
Понятие о теории графов
Теория графов представляет собой раздел математики, имеющий широкое практическое применение при решении многих проблем в различных областях науки и техники.
Любой граф состоит из двух групп элементов: точек и линий, соединяющих эти точки. Придерживаясь стандартной терминологии, точки будем называть вершинами или узлами графа, а линии – ребрами, если они не имеют направления, и дугами, если на них задано направление.
Графом G называется совокупность множества V, элементы которого называются вершинами, и множества А упорядоченных пар вершин, элементы которого называются ребрами. Предполагается, что как множество V, так и множество A содержат конечное число элементов.
Граф обозначается как G = (V, A), где V = {v1, v2, …, vn}, A = { a ij ½ i, j Î V}. При графическом представлении графа вершины обозначаются кружками, ребра – отрезками прямых, дуги – отрезками прямых с направляющими стрелками. Как правило, вершины обозначаются цифрами или буквами (например, 1, i, j), ребра – либо парой вида (i, j), либо a ij, указывающей начальную и конечную вершину ребра. Ребро с совпадающими начальной и конечной вершинами называется петлей.
Граф, в котором направления дуг не задаются, называется неориентированным. Граф, в котором направления дуг задаются, называется неориентированным. Граф, в котором имеются дуги и ребра, называется смешанным.
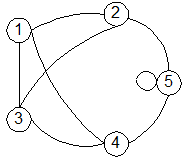 |  | ||
На рис.3.1 приведен пример неориентированного графа с множеством вершин V = {1, 2, 3, 4, 5} и множеством ребер A = { a 12, a 13, a 14, a 32, a 52, a 45, a 55, a 34}.
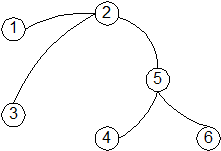
Рис.3.1. Пример графа Рис.3.2. Пример дерева
Путем, маршрутом или цепью из узла i в узел j на графе называется последовательность вершин и ребер, в которой конечный узел каждой дуги является начальным узлом следующей (исключая начальную и конечную вершину последовательности). При этом одно и то же ребро может встречаться в маршруте несколько раз. Если в маршруте графа нет ребер, предшествующих некоторой вершине, то она называется начальной вершиной маршрута. Если нет ребер, следующих за некоторой вершине, то такая вершина называется конечной (висящей) вершиной маршрута. Любая вершина графа, принадлежащая двум соседним ребрам, называется внутренней или промежуточной вершиной.
Пример пути из вершины 1 в вершину 4 (рис.3.1): 1, a 14, 4; 1, a 12, a 25, a 54, 4. Начальная вершина маршрута – 1, конечная вершина – 4.
Циклом называется конечный путь, начальный и конечный узлы которого совпадают.
Граф называется связным, если для любых двух различных вершин существует, по крайней мере, один соединяющий их путь. Частным случаем связных ориентированных и неориентированных графов являются деревья.
Деревом называется граф, не имеющий циклов. Пример дерева представлен на рис. 3.2. Корнем ориентированного дерева называется вершина, из которой ориентированные дуги могут только исходить.
Подграфом графа G = (V, A) называется граф G1 = (V1, A1), у которого V1Í V, AÍ A1, причем A1 = { a ij ½ i, j Î V1}.
Графы в памяти ЭВМ представляются в виде массивов или матриц.
Матрицей смежности ориентированного графа G называется квадратная матрица n ´ n (n – число вершин графа), в которой dij=1, если существует дуга от вершины i к j, и dij=0, если дуги нет. Если граф является неориентированным, то каждое ребро (i, j) Í A можно заменить двумя противоположно направленными дугами. При этом матрица смежности графа будет симметричной.
Матрицей инциденций ориентированного графа G называется квадратная матрица n ´ m (n – число вершин графа, m – количество дуг), в которой dik=1, если вершина i является начальной вершиной дуги k, dik=–1, если вершина i является конечной вершиной дуги k, и dij=0 в противном случае. Если граф является неориентированным, то dik=1, если узел i принадлежит ребру j и dij=0 в противном случае.