Несобственный интеграл от разрывной функции(2 рода)

Пусть функция f(x) непрерывна при a ≤ x < b и имеет точку разрыва при x =b. Тогда соответствующий несобственный интеграл от разрывной функции определяется формулой

(8)

и называется сходящимся или расходящимся в зависимости от того, существует или не существует предел правой части равенства (8).

Если существует функция F (x), непрерывная на отрезке [ a, b ] и такая, что F '(x) = f (x) при a ≤ x < b (обобщенная первообразная), то для несобственного интеграла (8) справедлива обобщенная формула Ньютона-Лейбница:

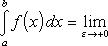
(9)

Если функция f(x) непрерывна при a< x ≤ b и имеет точку разрыва x = a, тогда

(10)

Если подынтегральная функция перестает быть ограниченной внутри отрезка интегрирования, например, при x = c, то эту точку " вырезают", а интеграл определяют в предположении, что F(x) - первообразная для f(x), так:

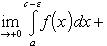
(11)

Если пределы в (9) существуют и конечны, то интеграл называется сходящимся, в противном случае - расходящимся.