Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вектор поляризации. Электрическое поле в диэлектриках
|
|
Для количественного описания свойств диэлектриков вводится физическая величина – вектор поляризации Р. Вектор поляризации определяется как предел отношения
, (2. 1)
– векторная сумма электрических моментов молекул, находящихся в этом элементе объема. Согласно (2. 1), вектор поляризации это электрический момент единицы объема диэлектрика. Вектор поляризации, являясь усредненной характеристикой диэлектрика, позволяет описать явления, не вдаваясь в подробности его микроструктуры.
В отсутствии внешнего электрического поля вектор поляризации равен нулю. Как показывает расчет, при не слишком больших полях вектор поляризации полярных и неполярных диэлектриков пропорционален напряженности электрического поля Е внутри диэлектрика:
, (2. 2)
где c – диэлектрическая восприимчивость (безразмерная величина), она определяется плотностью и внутренним строением диэлектриков. Для полярных диэлектриков c зависит от их температуры. Электрическое поле Е внутри диэлектрика (рис. 2.5), находящегося во внешнем поле Е 0, согласно принципа суперпозиции, определяется так
, (2. 3)
где Е / – напряженность электрического поля, созданного поляризационными зарядами диэлектрика.
Зная вектор поляризации, можно определить поляризационные заряды и наоборот. Рассмотрим в поле Е 0 однородный диэлектрик в виде наклонной призмы с основанием S и ребром l, параллельным Е 0 (рис. 2.6). В этом случае призма при однородной поляризации (вектор Р одинаков по всему диэлектрику) приобретет электрический момент р:
. (2. 4)
Объем призмы равен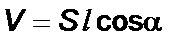 
, поэтому, электрический момент
единицы объема или численное значение вектора поляризации равно
,
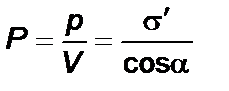откуда
, (2. 5)
где Рn – проекция вектора поляризации Р на направление внешней нормали к рассматриваемой поверхности.
Таким образом, поверхностная плотность поляризационных зарядов равна нормальной составляющей вектора поляризации в данной точке поверхности.
Можно показать, что поток вектора поляризации через любую замкнутую поверхность S (рис. 2.7) равен, взятой с обратным знаком, алгебраической сумме поляризационных зарядов, охватываемых данной поверхностью:
. (2. 6)