
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение показателя адиабаты воздуха
|
|
Цель работы.
Целью работы является углубление знаний в теории исследования термодинамических процессов, ознакомление с методикой опытного определения показателя адиабаты реальных газов, получения навыков в проведении теплотехнического эксперимента и его статистической обработки.
При выполнении работы производится экспериментальное определение численного значения показателя адиабаты воздуха и ознакомление со статистическими методами обработки результатов эксперимента.
Теоретическое положение.
Для исследования термодинамических процессов, характеризующих изменение состояния рабочего тела (газа или пара), используется ряд основных положений технической термодинамики. Первый закон термодинамики гласит, что все тело, подведенное к рабочему телу, затрачивается на изменение его внутренней энергии и совершение работы расширения:
 (1)
(1)
уравнение состояния рабочего тела:
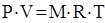 (2)
(2)
связывает основные параметры рабочего тела: Р – давление, Па; V – объем, занимаемый рабочим телом, м3; Т – абсолютную температуру, оК, (М – масса газа, кг; R – газовая постоянная, Дж/кг× К).
Путем совместного решения уравнения (1) и (2) получена зависимость, описывающая все реальные термодинамические процессы:
 P × Vn = const (3)
P × Vn = const (3)
Такое уравнение называется уравнением политропы или или политропного процесса, а n – показатель политропы.
Показатель политропы может принимать различные значения (от +0 до ±¥) и его величина будет соответствовать известным термодинамическим процессам, характеристики которых приведены в табл.2
Таблица 2
Характеристики основных термодинамических процессов
| Наименование процесса | Уравнение в P-V диаграмме | Показатель политропы | Уравнение 1 закона термодинамики | Значение теплоемкости, Дж/кг× К | Уравнение в T-S диаграмме |
| Политропный | P× Vn = const | n | dQ=dE+dL | C = Cn | 
|
| Изохорный | V = const | n = ±¥ | dQ = dE | C = Cv | 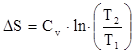
|
| Изобарный | P = const | n = 0 | dQ=dE+dL | C = Cp | 
|
| Изотермичес-кий | T = const | n = 1 | dQ = dL | C = ¥ | 
|
| Адиабатный (изоэнтропий-ный) | P× Vк = const | n = K | dQ = 0 | C = 0 | 
|
На рис.2. представлены изображения основных термодинамических процессов в P-V и T-S диаграммах, описываемых соответствующими уравнениями табл.2.
Так как работы расширения в термодинамическом процессе определяется по зависимости:
dL = P × dV, Дж (4)
то величина совершенной рабочим телом работы может быть определена в P-V диаграмме как площадь под кривой термодинамического процесса 1-2, то есть: 
 , Дж (5)
, Дж (5)

|
|

Рис. 2. Изображение термодинамических процессов в P-V (а) и T-S (б) диаграммах.
Для определения количества тепла, подведенного к рабочему телу, используется параметр состояния – энтропия S, Дж/кг× К:
 , Дж/кг× К (6)
, Дж/кг× К (6)
Таким образом, применяя T-S диаграмму, можно определить количество тепла, переданное рабочему телу, как площадь под кривой термодинамического процесса 1-2:
 , Дж (7)
, Дж (7)
Одним из наиболее часто встречающихся на практике термодинамических процессов является адиабатный процесс.
Адиабатным процессом называется термодинамический процесс изменения состояния рабочего тела, происходящий без обмена теплом с окружающей средой (dQ = 0).
В этом случае, работа расширения совершается за счет изменения внутренней энергии рабочего тела (dU = - dL).
Уравнение адиабатного процесса имеет вид:
P× Vn = const, (8)
где показатель адиабаты k, равный отношению изобарной теплоемкости cp к изохорной cv:
 > 1 (9)
> 1 (9)
Численное значение показателя адиабаты для идеального газа можно получить исходя из молекулярно-кинетической теории газов:
для одноатомного газа
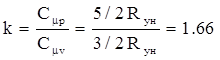 (10)
(10)
для двухатомного газа
 (11)
(11)
для многоатомного газа
 (12)
(12)
Oтсюда видно, что для идеальных газов величина k является постоянной, не зависящей от параметров состояния газа.
Связь между изобарной и изохорной теплоемкостями устанавливает уравнение Майера:
cp – cv = R(13)
Выразив из (5) cp, формулу (2.1) можно привести к виду:
 (14)
(14)
Поскольку для реальных газов теплоемкость Сv возрастает с увеличением температуры интенсивнее, чем Ср, то значение k с увеличением температуры уменьшается. Величина k для реальных газов одной атомности при прочих равных условиях имеет отличия. Так, например, для двухатомных газов: водород k=1, 41; азот k=1, 404; воздух k=1, 4.
Основные характеристики адиабатного процесса можно определить, зная численное значение показателя адиабаты (табл.3.).
Допустим, что условия опыта с достаточной степенью точности удовлетворяют уравнению состояния идеального газа
P V=M× R× T (15)
Представим сосуд, заполненный газом, имеющим параметры: давление P1 и температуру Т1, превышающие параметры окружающей среды.
Таблица 3.
| № | Характеристика | Уравнение |
| 1. | Связь между давлением и температурой. | 
|
| 2. | Связь между давлением и объемом. | 
|
| 3. | Связь между объемом и температурой. | 
|
| 4. | Работа расширения | 
|
| 5. | Техническая работа | 
|
| 6. | Теплоемкость | С1-2 = 0 |
За счет охлаждения стенок сосуда окружающей средой и отвода некого количества теплоты q1, температура газа станет равной температуре окружающей среды – Т2, а давление снизится до некого значения Р2 (процесс 1-2 рис.2.). Затем быстро выпустим газ из резервуара, соблюдая тем самым условия адиабатного расширения - отсутствие теплообмена с окружающей средой. В конце этого процесса (2-3) давление в сосуде станет равным давлению окружающей среды Р3, а температура понизится до Т3, меньшей Т2. Закроем сосуд и выждем некоторое время, в течении которого от окружающей среды к более холодному телу будет подведена теплота q2 (процесс 3-4). В результате температура возрастет до температуры окружающей среды (Т4 =Т2), а давление повысится до некого значения Р4.

Рис. 3. К определению показателя адиабаты газа.
Рассмотрим условный изотермический процесс 2-4. Так как для изотермического процесса уравнение (15) имеет вид
P V = const (16)
то
 (17)
(17)
а так как V3 = V4, то
 (18)
(18)
Используя уравнение адиабатного процесса:
PVk = const (19)
можно записать
 (20)
(20)
так как P2V2k = P3V3k.
Окончательно, прологарифмировав выражение (20), получим
 (21)
(21)
Эта формула будет в дальнейшем использоваться при обработке результатов.
Описание экспериментальной установки.
Экспериментальная установка (рис.4.) состоит из ресивера 8, в котором с помощью компрессора 6 создается избыточное давление, измеряемое датчиком давления 10. На линии нагнетания от компрессора к ресиверу расположен кран 7. Выпуск сжатого воздуха из ресивера производится через кран 11. Привод компрессора осуществляется от электродвигателя 5.
Для индикации напряжения предусмотрен вольтметр 4 и сигнальная лампа 3. Установка снабжена розеткой 220 В переменного тока 2.
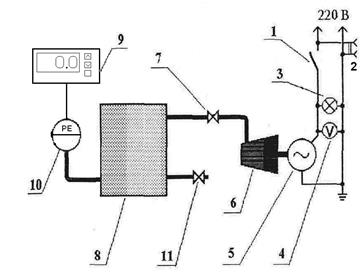
Рис. 4. Схема экспериментальной установки.
1- выключатель; 2- розетка 220 В; 3- сигнальная лампа; 4- вольтметр; 5- электродвигатель; 6- компрессор; 7- кран; 8- ресивер; 9 – показывающий прибор (измеритель), 10 – датчик давления (электрический преобразователь); 11- быстродействующий кран.
Обработка полученных данных и оформление отчета:
1) Pi=Ризбi+ Рбар (кПа) (Расчет Р2 и Р4 для каждого опыта)
Р2(1)= 13, 9+101, 4= 115, 3 P4(1)=3, 3+101, 4=104, 7
P2(2)=16, 2+101, 4= 117, 6 P4(2)=8, 2+101, 4= 109, 6
P2(3)=18, 3+101, 4= 119, 7 P4(3)=6, 2+101, 4= 107, 6
P2(4)=29, 4+101, 4= 130, 8 P4(4)=12, 2+101, 4=113, 6
P2(5)=35, 1+101, 4= 136, 5 P4(5)=12, 9+101, 4=114, 3
P2(6)=27, 1+101, 4= 128, 5 P4(6)=9+101, 4=110, 4
P2(7)=41, 8+101, 4= 143, 2 P4(7)=25, 9+101, 4=127, 3
P2(8)=30, 4+101, 4= 131, 8 P4(8)=11, 2+101, 4=112, 6
P2(9)=46, 7+101, 4= 148, 1 P4(9)=17, 6+101, 4=119
2)  ( расчет k для каждого опыта)
( расчет k для каждого опыта)
k1=  k2=
k2=  k3=
k3= 
k4=  k5=
k5= 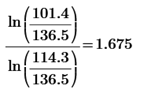 k6=
k6= 
k7=  k8=
k8=  k9 =
k9 = 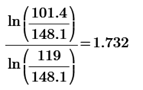
3)  ( расчет k среднего)
( расчет k среднего)

4) kотклi=│ ki-kcp│ ( расчет k отклонения от нормы, для каждого опыта)
k(1)=1.332-1.818=0.486 k(3)=1, 557-1.818=0.261 k(5)=1.675-1.818=0.143
k(2)=2.104-1.818=0.286 k(4)=1.806-1.818=0.012 k(6)=1.56-1.818=0.258
k(7)=2.933-1.818= 1.115 k(8)=1.665-1.818= 0.153 k(9)=1.732-1.818=0.086
5)  ( действительная ошибка эксперимента)
( действительная ошибка эксперимента)
qк=│ (1.4-1.818)/1.4│ =0.299*100%=29.9%
6)  ( Среднеквадратичная ошибка эксперимента)
( Среднеквадратичная ошибка эксперимента)
 0.023
0.023
Вывод о проделанной работе:
В ходе лабораторной работы было проведено ознакомление с методикой опытного определения показателя адиабаты реальных газов и ознакомление со статистическими методами обработки результатов эксперимента, после обработки полученных данных, была найдена адиабата реального газа равная k=1.818, действительная ошибка эксперимента составила 29.9%, среднеквадратичная ошибка составила 0.023.

