
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средние индексы. Общие индексы могут быть представлены не только в агрегатной форме, но и другим способом – путем вычисления средней величины из индивидуальных индексов.
|
|
Общие индексы могут быть представлены не только в агрегатной форме, но и другим способом – путем вычисления средней величины из индивидуальных индексов.
При расчете индексов часть необходимой информации может отсутствовать или базироваться на результатах выборочного наблюдения. Поэтому агрегатная форма общих индексов не применяется. В этом случае используется другая форма общих индексов – средневзвешенные индексы.
Таким образом, средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. Средний индекс всегда равен агрегатному индексу.
Средние индексы используются, когда отсутствуют данные по динамике признаков, но есть их относительное изменение. Средние индексы выводятся из агрегатных индексов и должны быть тождественны им. Для этого необходимо, чтобы слагаемые знаменателя агрегатного индекса были весами индивидуальных индексов.
На практике средние индексы рассчитываются в форме среднего арифметического и среднего гармонического индексов.
Средний арифметический индекс применяется в случае, если известно готовое произведение (выручка от реализации продукции) только базисного периода и изменение индивидуального индекса. Все преобразования производятся в числителе агрегатного индекса.
Преобразуем агрегатный индекс физического объема продукции в тождественную ему форму средних индексов:
 ;
;  ,
,  .
.
Таким образом, общий индекс физического объема продукции может быть выражен в форме средней арифметической из индивидуальных индексов физического объема продукции, взвешенных по стоимости продукции базисного периода  :
:
 - средний арифметический индекс физического объема продукции.
- средний арифметический индекс физического объема продукции.
Среднегармонический индекс применяется в случае, если известно готовое произведение (выручка от реализации продукции), а также изменение индивидуального индекса. Все преобразования производятся в знаменателе агрегатного индекса.
Преобразуем агрегатный индекс цены продукции в тождественную ему форму средних индексов:
 ;
;  ,
, 
Таким образом, общий индекс цены продукции может быть выражен в форме средней гармонической из индивидуальных индексов цены продукции, взвешенных по стоимости продукции текущего периода  :
:
 - средний гармонический индекс цены продукции.
- средний гармонический индекс цены продукции.
При построении средних индексов следует руководствоваться следующим правилом: для индекса количественного показателя используют формулу среднего арифметического индекса; для индекса качественного показателя (цена, себестоимость и т.д.) – формулу среднего гармонического индекса.
Например, запишем формулы среднего арифметического индекса физического объема продукции  и среднего гармонического индекса себестоимости
и среднего гармонического индекса себестоимости 


Средний арифметический индекс производительности труда определяется по формуле:
 .
.
Учитывая, что 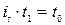 , можно перейти к агрегатному индексу трудоемкости продукции, в котором весами являются общие затраты времени на производство продукции в текущем периоде.
, можно перейти к агрегатному индексу трудоемкости продукции, в котором весами являются общие затраты времени на производство продукции в текущем периоде.
В средней арифметической форме также рассчитывается индекс производительности труда по трудоемкости, известный как индекс С.Г. Струмилина:
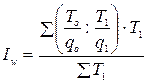 .
.
Индекс Струмилина показывает относительное изменение производительности труда.
Также средние индексы используются для анализа рынка ценных бумаг (индексы Доу-Джонса, Стэндарда и Пура).
9.5. Индексный анализ средних величин: индексы постоянного, переменного составов и структурных сдвигов
Индексы позволяют проанализировать изменения средних величин. При изучении динамики качественных показателей приходится определять изменение средней величины индексируемого показателя.
При этом на изменение средней величины показателя  одновременно могут влиять два фактора:
одновременно могут влиять два фактора:
1. изменение значений индексируемого показателя (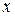 ) у отдельных единиц;
) у отдельных единиц;
2. изменение состава (структуры) совокупности ( ), т.е. весов.
), т.е. весов.
Под изменением структуры явления понимается изменение доли отдельных единиц совокупности в общей их численности ( ). Например, средняя зарплата может вырасти за счет роста оплаты труда сотрудников или за счет увеличения доли высокооплачиваемых сотрудников. Так как на изменение средней величины показателя
). Например, средняя зарплата может вырасти за счет роста оплаты труда сотрудников или за счет увеличения доли высокооплачиваемых сотрудников. Так как на изменение средней величины показателя  влияют два фактора
влияют два фактора  , то необходимо определить степень влияния каждого из них на общую динамику средней.
, то необходимо определить степень влияния каждого из них на общую динамику средней.
Поэтому, индексный метод в статистике также применяется для решения следующих задач:
· изучение динамики средних величин;
· выявление факторов, влияющих на динамику средних величин.
Динамику среднего уровня качественного показателя для однородной совокупности статистика изучает с помощью системы трех взаимосвязанных индексов:
· индекс переменного состава  ;
;
· индекс постоянного состава  ;
;
· индекс структурных сдвигов  .
.
Индекс переменного состава представляет собой соотношение средних величин показателя в текущем и базисном периодах.
В связи с тем, что средние величины рассчитываются, как правило, по формуле средней арифметической взвешенной, то индекс переменного состава для любых качественных показателей может быть построен следующим образом:
 .
.
Он характеризует динамику среднего показателя в однородной совокупности за счет влияния двух факторов:
1) изменение индексируемой величины 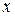 у отдельных единиц совокупности;
у отдельных единиц совокупности;
2) изменение структуры совокупности по изучаемому признаку (весов  ).
).
Индекс постоянного (фиксированного) состава отражает динамику среднего показателя лишь за счет изменения индексируемой величины 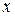 при фиксировании весов на уровне отчетного периода
при фиксировании весов на уровне отчетного периода  . В общем виде данный индекс можно записать следующим образом:
. В общем виде данный индекс можно записать следующим образом:
 .
.
Индекс постоянного состава может быть рассчитан и в агрегатной форме:

Индекс структурных сдвигов отражает динамику среднего показателя лишь за счет изменения весов  при фиксировании индексируемой величины на уровне базисного периода
при фиксировании индексируемой величины на уровне базисного периода  .
.
 .
.
Индекс структурных сдвигов можно получить, разделив индекс переменного состава на индекс постоянного состава:
 .
.
Этот индекс показывает, в какой степени изменение средней величины индексируемого показателя произошло за счет изменения структуры совокупности.
Таким образом, индексы переменного, постоянного состава и структурных сдвигов взаимосвязаны следующей формулой:

Если в качестве весов (соизмерителей) использовать показатели доли единиц совокупности в ее общей численности  , то система индексов может быть писана в следующем виде:
, то система индексов может быть писана в следующем виде:



где  ,
,  - доли отдельных единиц во всей совокупности в базисном и отчетном периодах соответственно (
- доли отдельных единиц во всей совокупности в базисном и отчетном периодах соответственно ( ).
).
Система индексов средних величин строится для изучения динамики среднего уровня цен, себестоимости, рентабельности, заработной платы, производительности труда, фондоотдачи и других признаков.
Также с помощью индексов средних величин можно отразить абсолютное изменение среднего уровня показателя за счет отдельных факторов. Например, общий абсолютный прирост (уменьшение) среднего уровня показателя в целом по совокупности находится как разность числителя и знаменателя индекса переменного состава:


Абсолютное изменение среднего уровня показателя в целом по совокупности можно показать за счет:
1) изменения значений индексируемого показателя (индекс постоянного состава):
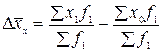 ;
; 
2) изменения структуры совокупности (индекс структурных сдвигов):
 ;
; 
В общем виде разложение индексов имеет вид:
 .
.
Рассмотрим применение индексного метода для анализа динамики средней цены  . При изучении динамики средней цены на однородную продукцию (услуги), реализуемую на разных рынках, можно рассчитать следующие индексы:
. При изучении динамики средней цены на однородную продукцию (услуги), реализуемую на разных рынках, можно рассчитать следующие индексы:
Индекс переменного состава: 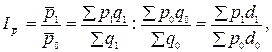
где: 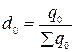 ,
,  .
.
Данный индекс показывает, относительное изменение средней цены определенного вида товара, реализованного по разным ценам и на разных рынках за счет двух факторов:
- изменения цен  на отдельных рынках;
на отдельных рынках;
- изменения количества (доли) товаров  , реализованных на разных рынках.
, реализованных на разных рынках.
Индекс постоянного состава: 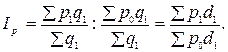
Этот индекс отражает среднее изменение цен на данный товар на всех рынках путем устранения влияния структурного фактора на динамику средних цен.
Индекс структурных сдвигов:  .
.
Этот индекс отражает изменение средней цены товара за счет структурного фактора, т.е. за счет изменения долей продукции, реализованной по разным ценам.
На основе данных индексов можно рассчитать абсолютное изменение средней цены в целом и за счет изменения отдельных факторов.
Абсолютное изменение средней цены за счет изменения индивидуальных цен и за счет изменения структуры совокупности (производства продукции):
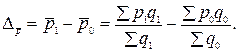
Абсолютное изменение средней цены за счет изменения индивидуальных цен при условии постоянства структуры совокупности (производства продукции):

Абсолютное изменение средней цены за счет изменения структуры совокупности (производства продукции):

Тогда общее изменение средней цены составит:

Индексы средних величин взаимосвязаны следующим образом:

Аналогично можно оценить динамику средней себестоимости, производительности труда, заработной платы.