Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка тесноты линейной связи
|
|
| Значение коэффициента корреляции | Теснота связи | Значение коэффициента детерминации, % |
| 0, 1 – 0, 3 | Слабая | до 10 |
| 0, 3 – 0, 5 | Умеренная | 10 – 25 |
| 0, 5 – 0, 7 | Заметная | 25 - 50 |
| 0, 7 – 0, 9 | Тесная | 50 - 80 |
| 0, 9 – 0, 99 | Весьма тесная | 80 и более |
Пример. Имеются данные по восьми однотипным фирмам о часовой оплате труда х и уровне текучести кадров у:
Часовая оплата труда, руб. ( )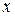
| ||||||||
Уровень текучести кадров, % ( )
|
Требуется:
1) найти уравнение регрессии 
(уравнение зависимости уровня текучести кадров от величины часовой оплаты труда);
2) измерить тесноту связи между признаками х и у.
Решение. Для решения задачи построим вспомогательную таблицу (табл. 10.4).
Таблица 10.4
Расчетная таблица для определения линейного коэффициента корреляции
| № п/п | Часовая оплата труда, руб. х | Уровень текучести кадров, % у | х2 | х у |
| у2 |
| 37, 25 | ||||||
| 33, 75 | ||||||
| 30, 25 | ||||||
| 26, 75 | ||||||
| 23, 25 | ||||||
| 19, 75 | ||||||
| 16, 25 | ||||||
| 12, 75 | ||||||
| Σ | ||||||
| Средняя величина | ||||||
| 
| 
| 
| 
|
1) Применяя метод приведения параллельных данных, видим, что с ростом значений признака х, значения признака у убывают. Поэтому с помощью графика зависимости у = у (х) можно предположить, что зависимость между х и у обратная, линейная.
Для построения линейного уравнения регрессии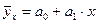 
найдем параметры а 0 и а 1:
= 
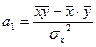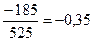- коэффициент регрессии, показывает, на сколько (в абсолютном выражении) изменяется значение результативного признака у при изменении факторного признака х на единицу.
уравнение регрессии
Подставляя в это уравнение последовательно значения х =30, 40, 50 и т.д., получаем выровненные (теоретические) значения результативного показателя (графа 6 таблицы).
Выровненные уровни показывают, каким теоретически должен быть средний уровень текучести кадров при данной часовой оплате труда хi . (при прочих равных условиях для всех предприятий).
2) Для измерения тесноты связи межу х и у применим формулу линейного коэффициента корреляции rху, т.к. связь линейная и число признаков равно двум.
2.1. Линейный коэффициент корреляции: 
.
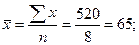
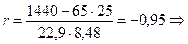связь обратная сильная, т.к. 
и 
.
2.2. Воспользуемся еще одной формулой линейного коэффициента корреляции:
Таким образом, между оплатой труда х и уровнем текучести кадров у существует сильная обратная связь, т.е. с увеличением оплаты труда текучесть кадров снижается.
Теснота связи при нелинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение рассчитывается по формуле:
,
где 
- межгрупповая дисперсия результативного признака, определяемая по формуле 
;
- общая дисперсия результативного признака, определяемая по формуле 
.
Теоретическое корреляционное отношение рассчитывается по формуле:
,
где - дисперсия эмпирических (фактических) значений результативного признака;
- остаточная дисперсия, отражающая вариацию результативного признака за счет факторов, не учтенных в уравнении регрессии. Значит, общая дисперсия эмпирического ряда равна сумме факторной и остаточной дисперсий: = 
+ 
.
В данном виде корреляционное отношение при криволинейной зависимости обычно называют индексом корреляции.
Корреляционное отношение 
показывает только силу связи и изменяется в пределах от 0 до 1 
. Направление связи определяют по групповым и корреляционным таблицам. Корреляционное отношение применимо для парной и множественной корреляции независимо от формы связи.
С помощью корреляционного отношения можно оценить тесноту связи при линейной и нелинейной зависимости между признаками (табл. 10.4.)
Таблица 10.4