Что такое логарифмическое преобразование. Когда применяется

Рассмотрим далее функции, которые являются нелинейными как по параметрам, так и по переменным:

Если обозначить , , , то уравнение (8) можно переписать в следующем виде:

.

Процедура оценивания регрессии следующая:

1. Вычисляется и 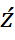для каждого наблюдения путем взятия логарифмов от исходных значений.

2. Оценивается регрессионная зависимость от 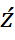. Коэффициент 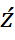будет представлять собой непосредственную оценку β. Постоянный член является оценкой , т.е. . Для получения оценки α необходимо вычислить .

Логарифмическое преобразование – переход от нелинейной и по переменным и по параметрам модели к логарифмической модели .

61. Опишите включение случайного члена в исходную модель, если преобразованная модель имеет вид

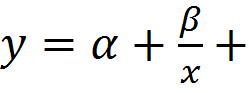Исходное (т.е. непреобразованное) уравнение будет иметь вид u

62. Опишите включение случайного члена в исходную модель, если преобразованная модель имеет вид

Если вернуться к исходному уравнению, то формулу следует переписать в виде , где v и u связаны соотношением . В этом случае соотношение имеет вид: , которое представляет собой уравнение 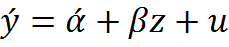с соответствующими изменениями определений. Следовательно, для получения аддитивного случайного члена в уравнении регрессии необходимо начать с мультипликативного случайного члена в исходном уравнении.

Случайный член v изменяет выражение путем увеличения или уменьшения его в случайной пропорции, а не на случайную величину. Если u =0, то , т.е. при v =1.