Распределение и трансформация токов и напряжений при несимметричных режимах.

Фазные токи и напряжения при несимметричных режимах проще всего находить путем суммирования их симметричных составляющих.

Поскольку рассматриваемые трехфазные схемы предполагаются выполненными симметрично, то распределение токов и напряжений каждой последовательности находят в схеме замещения одноименной последовательности, руководствуясь правилами и законами распределения токов и напряжений в линейных электрических цепях.

При определении фазных величин за трансформаторами нужно иметь в виду, что векторы токов и напряжений при переходе через трансформатор изменяются не только по величине, но и по фазе в зависимости от вида соединения его обмоток.

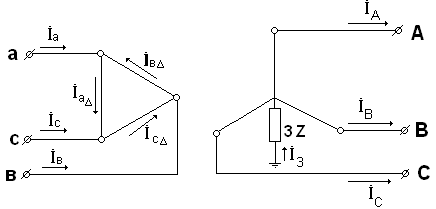
Обратимся к рис.4.6, где приведена принципиальная схема трансформатора с соединением обмоток звезда с заземленной нейтралью/треугольник.

Если число витков фазных обмоток соответственно равны 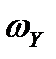и 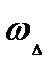, то линейный коэффициент трансформации будет .

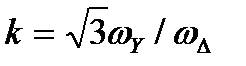При заданных фазных токах 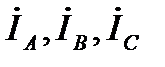в соответствии с принятыми на рис. 4.6 положительными направлениями для токов в линейных проводах за треугольником имеем:

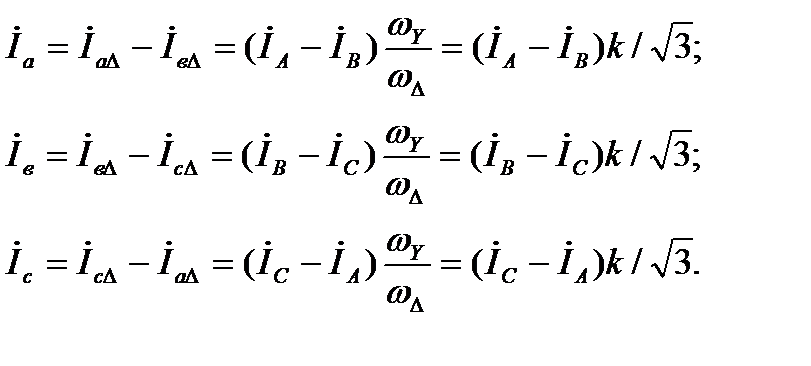(4.13)

Эту запись можно видоизменить, выразив токи через их симметричные составляющие.

Так, например для тока 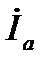получим

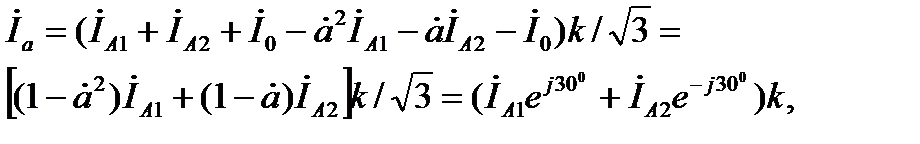(4.14)

откуда, в частности, видно, что линейные токи на стороне обмотки трансформатора, соединенной в треугольник, не содержат составляющих нулевой последовательсти.

Аналогично могут быть найдены напряжения на стороне обмотки трансформатора, соединенной в треугольник.

Если 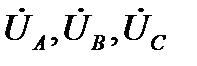- фазные напряжения со стороны звезды, включающие в себя и падения напряжения в самом трансформаторе, то искомые фазные напряжения со стороны треугольника будут:

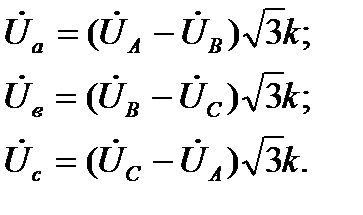(4.15)

При выражении напряжений через симметричные составляющие, например, для напряжения 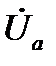, будем иметь:

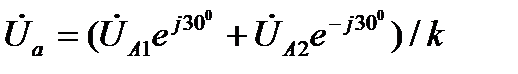. (4.16)

Структура выражений (4.14) и (4.16) показывает, что при переходе со стороны звезды на сторону треугольника трансформатора, обмотки которого соединены по группе векторы прямой последовательности повертываются на 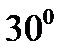в направлении вращения векторов (против направления движения стрелки часов), а векторы обратной последовательности – на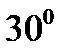

в противоположном направлении (рис.4.7-4.8).

При переходе через трансформатор в обратном направлении угловые смещения симметричных составляющих меняют свой знак на противоположный.

Рис.4.7. Рис.4.8.