
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Цели и задачи исследования математических моделей систем
|
|
Математическое моделирование – создание математического описания реального объекта и изучение этого описания.
Первоначально любые расчеты по моделям производились вручную. По мере развития вычислительных устройств, эти устройства применялись для ускорения расчетов.
Компьютер позволяет использовать его как средство автоматизации научной работы и для решения сложных расчетных задач используют различные специализированные программы.
В то же время, в научной работе встречается широкий спектр несложных математических задач, для решения которых можно использовать универсальные профессиональные средства.
К таким несложным задачам относятся, например, следующие:
подготовка научно-технических документов, содержащих текст и формулы, записанные в привычной для специалистов форме;
вычисление результатов математических операций, в которых участвуют числовые константы, переменные и размерные физические величины;
операции с векторами и матрицами;
решение уравнений и систем уравнений (неравенств);
статистические расчеты и анализ данных;
построение двумерных и трехмерных графиков;
тождественные преобразования выражений (в том числе упрощение), аналитическое решение уравнений и систем;
дифференцирование и интегрирование, аналитическое и численное;
решение дифференциальных уравнений;
проведение серий расчетов с разными значениями начальных условий и других параметров.
Для работы с математическими моделями используются прикладные пакеты математического моделирования.
Наиболее частой, если не единственной, целью построения математической модели является задача оптимизации моделируемого объекта.
26, 27 Классификация математических моделей.
 1)
1)
Система есть совокупность взаимосвязанных элементов, в определенном смысле обособленная от окружающей среды и взаимодействующая с ней как целое.
 Для сложных систем характерно наличие большого числа взаимосвязанных между собой элементов:
Для сложных систем характерно наличие большого числа взаимосвязанных между собой элементов:
Схема электронной системы
Например: система состоит из 3 блоков (N = 3) каждый блок находится в 2-х состояниях (М = 2 вкл. и выкл.) => S=23=8 состояний. Число связей = 6.
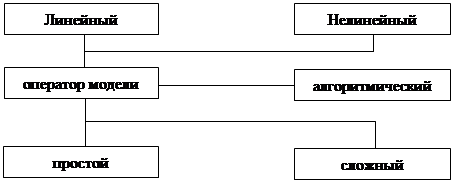
2) Выше отмечалось, что любая математическая модель рассматривается как оператор А, который является алгоритмом или определяет совокупность уравнений.
 |
| функция | обыкновенное дифференциальное уравнение | алгебраические дифференциальные уравнения в частных производных |
Если оператор обеспечивает линейную зависимость выходных параметров Y от значений входных параметров Х, то математическая модель называется линейной.

Схема нелинейной модели
 |
Методы исследования таких моделей прогрессируют, например: синергетика – наука о сложных самоорганизующих системах
В случае, когда оператор модели является алгебраическим, отображающим функциональную зависимость выходных параметров Y от входных Х модель называется простой. Модель, включающая системы дифференциальных и интегральных соотношений называется сложной.
3) Классификация в зависимости от параметров.
4) Классификация математических моделей в зависимости от методов реализации.
 | |||
 |
Метод модели относится к аналитическому, если он позволяет получить выходные
параметры в виде аналитических выражений.
Частым случаем аналитических выражений является алгебраические выражения в которых используется конечное или счетное число арифметических операций.
5) Классификация моделей в зависимости от целей моделирования.
Целью дискрептивных моделей (описание) является установление законов изменения параметров модели.
Оптимизационные модели предназначены для определения оптимальных параметров моделируемого объекта или для поиска оптимального режима управления процессом.
Управленческие модели применяются для принятия эффективных управленческих решений в различных областях деятельности.

28. Этапы математического моделирования.
Этапы построения математической модели:
1) Обследование модели, постановка задачи.
2) Концептуальная и математическая постановка задачи.
3) Анализ модели.
4) Выбор метода решения задачи (аналитический, прочие методы).
5) Проверка адекватности модели.
6) Практическое использование построенной модели.