
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 1.
|
|
Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий:
а). Построить большой завод стоимостью Ст1 = 500 тысяч у.е. При этом варианте возможны большой спрос (годовой доход в размере Д1 = 200 тысяч у.е. в течение следующих 5 лет) с вероятностью p1 = 0, 7 и низкий спрос (ежегодные убытки Д2 = 90 тысяч у.е.) с вероятностью р2 = 0, 3.
б). Построить маленький завод стоимостью Ст2 = 300 тысяч у.е. При этом варианте возможны большой спрос (годовой доход в размере Д3 = 100 тысяч у.е. в течение следующих 5 лет) с вероятностью p3 = 0, 7 и низкий спрос (ежегодные убытки Д4 = 40 тысяч у.е.) с вероятностью р4 = 0, 3.
в). Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью p5 = 0, 4 и p6 = 0, 6 соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, а вероятности большого и низкого спроса меняются на p7 = 0, 8 и р8 = 0, 2 соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет.
Нарисовав дерево решений, определим наиболее эффективную последовательность действий, основываясь на ожидаемых доходах.
Решение.
Строим дерево решений.
Строим узел 1, из которого исходят три заявленные в условии варианты. Обозначаем эти ветви пунктиром, поскольку это – возможные решения.
На концах ветвей ставим узлы-исходы, заключаем их в круг и обозначаем буквами А, В и т.д. Рисуем из этих узлов-исходов ветви с возможными исходами при выборе того или иного варианта из условия. Под каждой ветвью подписываем вероятности соответствующих исходов. На концах каждой ветви, не закрытой новым узлом, выставляем доходы и убытки, умноженные (исходя из условия) на время (годы из условия). На ветвях (возможные решения) ставим стоимость строительства со знаком «-», так как это расходы компании. Убытки на концах «открытых» ветвей также пишем со знаком «-».

Рис.1 – Дерево решений для примера 1. Первый этап построения
Далее считаем ожидаемые стоимостные оценки узлов.
Ожидаемая стоимостная оценка узла А равна:
ЕМV(А) = 0, 8 х 1000 + 0, 2 х (-450) -500 = 210.
EMV(B) = 0, 8 х 500 + 0, 2 х (-200) - 300 = 60.
EMV(D) = 0, 9 x 800 + 0, 1 x (-360) - 500 = 184.
EMV(E) = 0, 9 x 400 + 0, 1 х (-160) - 300 = 44.
Для узлов принятия решения 2 (второй уровень, условно) выбираем максимальную оценку:
EMV(2) = max {EMV(D), EMV(E)} = max {184, 44} = 184 = EMV(D).
Поэтому в узле 2 отбрасываем возможное решение «маленький завод».
EMV(C) = 0, 7 x 184 + 0, 3 x 0 = 128, 8.
Для узла принятия решения 1 – узла принятия окончательного решения, аналогично выбираем максимальную оценку на других узлах.
EMV(1) = max {ЕМV(A), EMV(B), EMV(C)} = max {210; 60; 128, 8} = 210 = EMV(А).
Поэтому в узле 1 выбираем решение «большой завод». Исследование проводить не нужно. Строим большой завод. Ожидаемая стоимостная оценка этого наилучшего решения равна 210 тысяч у.е.
Ответ: наиболее подходящее решение – решение строить большой завод.
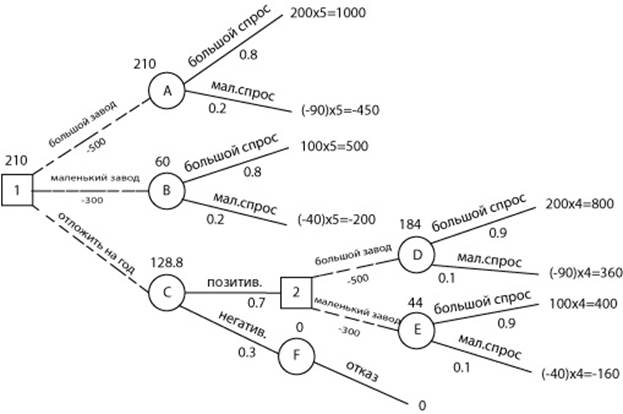
Рис.2 – Дерево решений со стоимостными оценками
В рассмотренном примере мы произвели отсечение ветвей в узле 2. И далее в задаче мы отсекаем те ветви и узлы, стоимостные оценки которых не приемлемы для принятия наиболее выгодного решения.
Способ 2. Применяется в случаях, если необходимо провести исследование по каким-либо атрибутам. Чаще всего, здесь фигурируют понятия таблиц, как в базах данных. Проще говоря, деревья решений разбивают данные на группы на основе значений переменных, в результате чего возникает иерархия операторов " ЕСЛИ - ТО", которые классифицируют данные.
И такие деревья решений называются деревьями классификаций.
Цель построения деревьев классификации заключается в предсказании (или объяснении) значений категориальной зависимой переменной, и поэтому используемые методы тесно связаны с более традиционными методами, например, кластерного анализа [1]. Широкая сфера применимости деревьев классификации делает их весьма привлекательным инструментом анализа данных.
Что же такое деревья классификации? Рассмотрим простой пример.
Пример 2. Необходимо придумать устройство, которое отсортирует коллекцию монет по их достоинству (например, 1, 2, 3 и 5 копеек). Предположим, что какое-то из измерений монет, например - диаметр, известен и, поэтому, может быть использован для построения иерархического устройства сортировки монет. Заставим монеты катиться по узкому желобу, в котором прорезана щель размером с однокопеечную монету. Если монета провалилась в щель, то это 1 копейка; в противном случае она продолжает катиться дальше по желобу и натыкается на щель для двухкопеечной монеты; если она туда провалится, то это 2 копейки, если нет (значит это 3 или 5 копеек) - покатится дальше, и так далее. Таким образом, мы построили дерево классификации. Решающее правило, реализованное в этом дереве классификации, позволяет эффективно рассортировать горсть монет, а в общем случае применимо к широкому спектру задач классификации. [2]
Деревья классификации идеально приспособлены для графического представления, и поэтому сделанные на их основе выводы гораздо легче интерпретировать, чем если бы они были представлены только в числовой форме.
В печатных изданиях приводится ряд примеров применения деревьев классификации. Один из них посвящен диагностике больных, поступающих в стационар с сердечным приступом. В приемном отделении у них измеряют несколько десятков показателей (частоту пульса, кровяное давление и т.д.). Одновременно в базу данных заносится много другой информации о больном (возраст, перенесенные болезни и др.). Из последующей истории пациента можно, в частности, выделить такой показатель: прожил ли он 30 дней (или более) после приступа. Для разработки методов лечения больных с сердечной недостаточностью было бы весьма полезно научиться по данным первичного обследования выявлять пациентов с высокой степенью риска (тех, кто, вероятнее всего, не сможет прожить больше 30 дней, например). Одно из деревьев классификации, построенных авторами для этой задачи, представляло собой бинарное дерево классификации, и его можно описать следующей фразой: " Если нижнее давление у пациента в течение первых суток не опускается ниже 91, то, если его возраст превосходит 62.5 года, то, если у него наблюдается синусоидальная тахикардия, то в этом и только в этом случае следует ожидать, что пациент не сможет прожить 30 дней." Из этого предложения несложно представить себе соответствующее " дерево" решений. Как видим, в таком дереве вопросы задаются последовательно (иерархически), и окончательное решение зависит от ответов на все предыдущие вопросы. Иерархическое строение дерева классификации - одно из наиболее важных его свойств.