Модуль і аргумент комплексного числа.

Довжина вектора, що зображає|змальовує| комплексне число, називається модулем цього комплексного числа. Модуль всякого|усякого| комплексного числа, не рівного нулю, є позитивне число. Модуль комплексного числа а + bi позначається|значиться| | а + bi |, а також буквою|літерою| r. З|із| креслення видно|показно|, що

r = | а + bi | = a² + b²

Модуль дійсного числа співпадає|збігається| з|із| його абсолютним значенням. Зв'язані комплексні числа а + bi u а – bi мають один і той же модуль.

Геометричний сенс|зміст, рація| складання і віднімання комплексних чисел.

Хай|нехай| вектори ОМ і ОМ’ (фіг. 4) зображають|змальовують| комплексні числа z= x + yi u z’ = x’ + y’i. З|із| точки М проведемо вектор МК|, рівний OM’. Тоді вектор ОК| зображає|змальовує| суму даних комплексних чисел.

Побудований|споруджений| вказаним чином вектор ОК| називається геометричною сумою векторів ОМ і ОМ’.

Отже, сума двох комплексних чисел представляється сумою векторів, що зображають|змальовують| окремі доданки.

Довжина сторони ОК| трикутника ОМК| менше суми і більше різниці довжин ОМ і МК|. Тому

||z| - |z’|| < |z + z’| < |z| + |z’|.

Рівність має сенс тільки|лише| в тих випадках, коли вектори ОМ і ОМ’ мають однакові (фиг.5) або протилежні (фиг.6) напрями|направлення|. У першому випадку |OM| + |OM’| = |OK|, тобто |z +z’|=|z| + + |z’|. У другому випадку |z + z’|=||z| - |z’||.

Завдання|задавання| для перевірки знань:

5. Як можна зобразити|змалювати| на площині|плоскості| число 5-3i, 3+8i-4i?

6. Що таке модуль комплексного числа?

7. Що таке аргумент комплексного числа?

8. Який геометричний сенс|зміст, рацію| мають складання і віднімання комплексних чисел?

Література:

2. А.Д. Мышкис «Лекции по высшей математике» стр.221-222

Розділ: «Комплексні числа»

Матеріал для самостійного вивчення

Тема: Тригонометрична й показова форми комплексного числа

Ціль: Розглянути зі студентамитригонометричну й показову форми комплексного числа

План: 1. Тригонометрична форма комплексного числа

2. Показова форма комплексного числа

Тригонометрична форма комплексного числа.

Абсциса а й ордината b комплексного числа a + bi виражаються через модуль r і аргумент q. Формулами

a = r cos q; b = r sin q.

Тому всяке комплексне число можна представити у вигляді r(cos q + i sin q), де r > 0.

Це вираження називається нормальною тригонометричною формою або, коротше тригонометричною формою комплексного числа.

Показова форма комплексного числа

Ця формула називається формулою Ейлера:

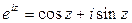(1)

Застосовуються також формула:

(2)

а також формули:

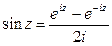(3)

Всі ці формули були знайдені Ейлером в 1743 р.

З формули Ейлера на основі властивості одержуємо вираження для експоненти з будь-яким комплексним показником

(4)

Порівняння із тригонометричною формою показує, що

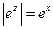
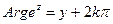(5)

Зокрема, видно, що завжди , тобто 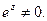якщо у формулі (4) замість 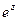писати z, те на підставі (5) одержимо

.

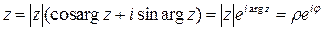Така «показова форма» комплексного числа буває зручна для виконання над ним алгебраїчних дій.

З формул (2) випливають співвідношення між тригонометричними й гіперболічними функціями: 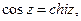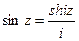, тобто . Звідси, підставивши iz замість z, одержимо cosiz=chz, siniz=ishz.

Завдання для перевірки знань:

1. Тригонометрична форма комплексного числа

2. Показова форма комплексного числа

Література:

3. А.Д. Мышкис «Лекции по высшей математике» стр.222-223

Розділ: «Комплексні числа»

Лекція

Тема: Дії з|із| комплексними числами у формі, алгебри

Мета|ціль|: Набути навичок при виконанні арифметичних операцій над комплексними числами

План: 1. Складання комплексних чисел

2. Віднімання комплексних чисел

3. Множення комплексних чисел

4. Ділення|поділка, розподіл, поділ| комплексних чисел