
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ділення|поділка,розподіл,поділ| комплексних чисел.
|
|
Відповідно до визначення ділення|поділки, розподілу, поділу| дійсних чисел встановлюється наступне|таке| визначення.
Визначення. Розділити комплексне число а + bi на комплексне число a’ + b’i – означає|значить| знайти таке число x + yi, яке, будучи помножено на дільника, дасть ділиме.
Якщо дільник не рівний нулю, то ділення|поділка, розподіл, поділ| завжди можливе, і приватне єдино (доказ дивися в зауваженні 2). На практиці приватне найзручніше знаходити|находити| таким чином.
Приклад|зразок| 1. Знайти приватне (7 – 4i): (3 + 2i).
Записавши дріб (7 – 4i)/(3 + 2i), розширюємо її на число 3 – 2i, зв'язане з 3 + 2i. Одержимо|отримаємо|:
((7 – 4i)(3 - 2i))/((3 + 2i)(3 – 2i)) = (13 – 26i)/13 = 1 – 2i.
Приклад|зразок| 1 | параграфа дає перевірку.
Приклад|зразок| 2. (-2 +5i)/(-3 –4i) = ((-2 + 5i)(-3 – 4i))/((-3 – 4i)(-3 + 4i)) = (-14 –23i)/25 = -0, 56 – 0.92i.
Щоб довести, що права частина|частка| дійсно є|з'являється, являється| приватною, досить множити її a’ + b’. Одержимо|отримаємо| а + bi.
З а м е ч а н і е 1. Формулу (1) було б прийняти за визначення ділення|поділки, розподілу, поділу|.
З а м е ч а н і е 2. Формулу (1) можна вивести ще таким чином. Згідно визначенню, ми повинні мати: (a’ + b’i)(x + yi) = а + bi. Означає|значить|, повинні задовольнятися наступні|слідуючі| два рівняння:
a’x – b’y = а; b’x + a’y = b.
якщо a’/b’ = -b’/a’, тобто якщо a’2 + b’2 = 0.
Залишається розглянути|розгледіти| випадок a’2 + b’ 2 = 0. Він можливий лише тоді, коли a’ = 0 і b’ = 0, тобто коли дільник a’ + b’i рівний нулю. Якщо при цьому і ділиме а + bi рівне нулю, то приватне невизначене. Якщо ж ділиме не рівне нулю, то приватне не існує (говорять, що воно рівне нескінченності).
Завдання|задавання| для перевірки знань:
1. Складання комплексних чисел
2. Віднімання комплексних чисел
3. Множення комплексних чисел
4. Ділення|поділка, розподіл, поділ| комплексних чисел
Література:
4. А.Д. Мышкис «Лекции по высшей математике» стр.220-223
Розділ: «Комплексні числа»
Матеріал для самостійного вивчення
Тема: Застосування комплексних чисел в електротехнічних розрахунках
Ціль: Розглянути зі студентамизастосування комплексних чисел в електротехнічних розрахунках
План: 1. Застосування до опису коливань.
2. Поняття комплексної напруги й комплексної сили.
Застосування до опису коливань.
Функцію

 (1)
(1)
Зручно застосувати для дослідження гармонійних коливань. Для цього треба помітити, що величина (1) має модуль М и аргумент  , тобто вона представима вектором постійної довжини, що рівномірно обертається з кутовою швидкістю
, тобто вона представима вектором постійної довжини, що рівномірно обертається з кутовою швидкістю  .
.
Розглянемо, наприклад, накладення коливань, що відбуваються з однаковою частотою. Нехай треба скласти дві величини:  і
і 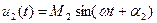 . Для цього введемо відповідні комплексні величини
. Для цього введемо відповідні комплексні величини  й
й  , у яких
, у яких  і
і  будуть служити мнимими частинами. Вектори
будуть служити мнимими частинами. Вектори  й
й  рівномірно обертаються з кутовою швидкістю
рівномірно обертаються з кутовою швидкістю  ; виходить, і вектор
; виходить, і вектор  рівномірно обертається з тією же швидкістю й тому його можна представити у вигляді (1). Щоб знайти М и
рівномірно обертається з тією же швидкістю й тому його можна представити у вигляді (1). Щоб знайти М и 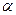 , досить розглянути картину в момент t=0, з її, проектуючи на осі координат, одержимо
, досить розглянути картину в момент t=0, з її, проектуючи на осі координат, одержимо
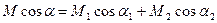
 (2)
(2)
Взявши мниму частину від  , ми приходимо остаточно до висновку, що
, ми приходимо остаточно до висновку, що  , де М и
, де М и 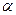 перебувають із рівностей (2).
перебувають із рівностей (2).
Аналогічний результат виходить при накладенні будь-якого числа гармонійних коливань, що відбуваються з однаковою частотою.
Перевага експоненти (1) перед тригонометричними функціями особливо проявляється при диференціюванні:
 (3)
(3)
У цьому випадку виходить вектор, що також рівномірно обертається з кутовою швидкістю  , але випереджальний U на 90º і модуль, що має, у
, але випереджальний U на 90º і модуль, що має, у  раз більший. При подальших диференціюваннях ці поворот і розтягання повторюються.
раз більший. При подальших диференціюваннях ці поворот і розтягання повторюються.
Покажемо застосування функцій виду (1) до розрахунку сталого струму в ланцюзі з активним опором і індуктивністю, якщо до ланцюга підключене джерело напруги, що міняється за гармонійним законом 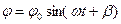 . При цьому в ланцюзі виникає струм, що також міняється за гармонійним законом
. При цьому в ланцюзі виникає струм, що також міняється за гармонійним законом  , однак
, однак  і
і 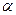 нам заздалегідь не відомі. Дорівнюючи
нам заздалегідь не відомі. Дорівнюючи 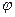 сумі падінь напруг на R і L на основі відомих у фізику законів, одержуємо основне рівняння задачі
сумі падінь напруг на R і L на основі відомих у фізику законів, одержуємо основне рівняння задачі 
Введемо поняття комплексної напруги й комплексної сили струму по формулах  ,
,  ; «справжні» напруга й сила струму служать мнимими частинами цих виражень. Для одержання j треба вирішити рівняння
; «справжні» напруга й сила струму служать мнимими частинами цих виражень. Для одержання j треба вирішити рівняння  , від відповіді взяти мниму частину. Відповідно до формули (3) одержуємо
, від відповіді взяти мниму частину. Відповідно до формули (3) одержуємо  , тобто
, тобто  (4)
(4)
Ми бачимо, що індуктивність L можна витлумачити як якийсь опір, чисельно рівне  ; це значення називається гаданим опором або імпедансом елемента L. Записавши
; це значення називається гаданим опором або імпедансом елемента L. Записавши  в показовій формі з (4) одержимо
в показовій формі з (4) одержимо

Завдання для перевірки знань:
1. Застосування до опису коливань.
2. Поняття комплексної напруги й комплексної сили
Література:
5. А.Д. Мышкис «Лекции по высшей математике» стр.223-224