
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Напряжение и потенциал электростатического поля
|
|
Основные величины, характеризующие электростатическое поле – это напряженность и потенциал. Напряженность электростатического поля – величина векторная и определяется в каждой точке поля значением и направлением. Потенциал – величина скалярная и определяется в каждой точке поля некоторым числом. Поле считается определенным, если известен потенциал во всех точках поля, или известен закон изменения напряженности.
Поместим в электрическое поле некоторый заряд q. На заряд будет действовать сила, и он будет перемещаться из т. 1 в т. 2 по пути 1-3-2.

Так как направление силы  , может не совпадать с элементом пути
, может не совпадать с элементом пути 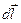 , то работа по перемещению заряда на пути
, то работа по перемещению заряда на пути 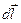 определится скалярным произведением силы на элемент пути:
определится скалярным произведением силы на элемент пути:

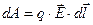
Заряд может быть любым, поэтому примем его равным 1(единичный заряд).
 – скалярное произведение
– скалярное произведение
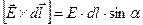 – векторное произведение
– векторное произведение
Или в интегральной форме:

Под разностью потенциалов (напряжением) принято понимать работу, затрачиваемую силами поля при переносе единичного заряда из начальной точки 1 в конечную точку 2.

Предположим, что в точке W находится точечный заряд q1, создающий поле, а из точки 1 в т.2 через т.3 перемещается единичный положительный заряд q =1.
 (см. рисунок)
(см. рисунок)

Таким образом, разность потенциалов между исходной и конечной точкой зависит только от положения этих точек и не зависит от пути, по которому происходило перемещение.
Если перемещать заряд по замкнутому контуру1-3-2-4-1, то исходная и конечная точки пути совпадут, и разность потенциалов будет равна нулю.

Условие потенциальности электростатического поля в интегральной форме
На основании теоремы Стокса заменим циркуляцию по замкнутому контуру поверхностным интегралом:



Условие потенциальности электростатического поля в дифференциальной форме
Потенциальное поле – некоторая ограниченная область пространства, каждая точка которой имеет свой постоянный и неизменный во времени потенциал.
Если поле потенциально, то оно безвихревое.
Если потенциал конечной точки равен 0, то получим уравнение потенциала электростатического поля:

За точку нулевого потенциала можно принять любую точку поля. Нередко принимают, что точка с нулевым потенциалом лежит в бесконечности, тогда постоянная интегрирования С =0, в итоге получим:

Потенциал произвольной точки поля можно определить как работу, совершаемую силами поля по переносу единичного положительного заряда из данной точки поля в ту точку поля, потенциал которой равен нулю (в бесконечность) и на оборот.