
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Умова-Пойтинга
|
|
Теорема Умова-Пойтинга выражает закон сохранения энергии. Она связывает изменение энергии в некотором объёме с потоком энергии через поверхность, ограничивающую этот объём.
1)  - первое уравнение Максвелла
- первое уравнение Максвелла
2)  - второе уравнение Максвелла
- второе уравнение Максвелла
Для того, чтобы получить выражение, в которое бы вошла полная энергия в каком-то объёме dV, необходимо умножить первое уравнение Максвелла на  , а второе уравнение Максвелла на
, а второе уравнение Максвелла на  .
.


Вычтем из уравнения (1) уравнение (2).
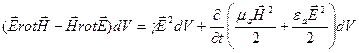
 видно, что левая часть есть дивергенция со знаком «-»
видно, что левая часть есть дивергенция со знаком «-»

Для сокращения векторное произведение  на
на  обозначим через
обозначим через
 - вектор Пойтинга
- вектор Пойтинга 
Таким образом, вектор Пойтинга имеет размерность мощности (или энергии в единицу времени), отнесенной к единице поверхности и направление его совпадает с направлением движения острия правоходного винта, если головку последнего вращать по кратчайшему расстоянию от  к
к  .
.


Рассмотрим некоторый конечный объем

Заменим объемный интеграл на поверхностный на основании теоремы Остроградского - Гаусса


 - запас электромагнитной энергии.
- запас электромагнитной энергии.
 - теорема Умова-Пойтинга
- теорема Умова-Пойтинга
 - мощность тепловых потерь - энергия, выделяющаяся в виде теплоты в единицу времени в единице объема.
- мощность тепловых потерь - энергия, выделяющаяся в виде теплоты в единицу времени в единице объема.
 - скорость изменения запаса электромагнитной энергии.
- скорость изменения запаса электромагнитной энергии.
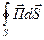 - поток вектора Пойтинга, входящий в поверхность S или мощность, передаваемая внутрь поверхности. Размерность ВА.
- поток вектора Пойтинга, входящий в поверхность S или мощность, передаваемая внутрь поверхности. Размерность ВА.
Так как вектор  направлен внутрь объема, а нормаль направлена перпендикулярно наружу, то угол между нормалью и вектором
направлен внутрь объема, а нормаль направлена перпендикулярно наружу, то угол между нормалью и вектором  будет больше 900, поэтому скалярное произведение вектора Пойтинга на нормаль всегда будет иметь отрицательное значение, следовательно, знак «-» в левой части уравнения делает эту часть положительной.
будет больше 900, поэтому скалярное произведение вектора Пойтинга на нормаль всегда будет иметь отрицательное значение, следовательно, знак «-» в левой части уравнения делает эту часть положительной.

Вывод:
Теорему Умова-Пойнтинга трактуют, как уравнение энергетического баланса: левая часть - это мощность, доставляемая в виде вектора Пойтинга внутрь некоторого объема; правая часть - это энергия, расходуемая и запасаемая в единице времени в единице объема.
Пример.
Энергия постоянного тока передается по коаксиальному кабелю. Между жилой и оболочкой пространство заполнено идеальным диэлектриком. R1 – радиус жилы, R2 – радиус оболочки. Проводимость материала жилы равна бесконечности  , т.е. потерь нет
, т.е. потерь нет  .
.

R1 < R < R2
Вектор Пойтинга направлен от нас (от источника у нагрузке). Так как  , то:
, то:

Из закона полного тока 
Вектор напряжённости в диэлектрике при постоянном токе определяется также, как и в условиях электростатики

 – напряжение между жилой и оболочкой
– напряжение между жилой и оболочкой
 – полный заряд жилы на длине l
– полный заряд жилы на длине l

Вектор Пойнтинга в некоторой точке диэлектрика

Поток вектора Пойнтинга

Так как вектор Пойнтинга  и нормаль
и нормаль  расположены под углом 180 градусов, то избавляемся от скалярного произведения
расположены под углом 180 градусов, то избавляемся от скалярного произведения  и знака «-»
и знака «-»


Вывод:
Получили, что вся мощность передается по диэлектрику, следовательно, энергия по жиле и оболочке не передается. Проводник (жила – оболочка), это каналы, по которым проходит ток, а так же организаторы структуры поля. Если диэлектрик не идеален, то энергия на покрытие тепловых потерь частично поступает в проводник из диэлектрика (проводимость конечна), следовательно, напряженность будет направлена по току, тогда поток вектора Пойтинга будет направлен через боковую поверхность внутрь провода.