Практична робота № 1

Розрахунок рівнозмінного та рівномірного рухів. Побудова графіків

Мета: розглянути основні характеристики рівномірного та рівнозмінного рухів; навчитися розраховувати різні види рухів та будувати їх графіки.

Основні теоретичні відомості

Розташування точки на траєкторії при прямолінійному русі визначається її координатою x. Вираз виду x=f(x) називається кінетичним рівнянням руху матеріальної точки. Якщо точка рухається по прямій в одному напрямку, то координата співпадає з довжиною шляху, який пройшло тіло від початку координат. Якщо в певний момент часу точка змінює напрям руху на протилежний, то координата і шлях не співпадають, оскільки координата зменшується, а шлях продовжує збільшуватися.

Середня швидкість:

= ,

де Δ x – зміна координати x за проміжок часу Δ t.

Дана формула втрачає зміст, якщо інтервал Δ x містить точку повернення, тобто точку, в якій рух змінюється на зворотній. У цьому випадку користуються формулою:

= .

Миттєва швидкість:

𝜗 = .

Середнє прискорення:

= ,

де Δ 𝜗 – зміна швидкості за проміжок часу Δ t.

Миттєве прискорення:

a = = .

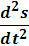Прискорення при рівнозмінному русі а = соnst. Якщо а< 0, то рух рівносповільнений, якщо а > 0, то рух рівноприскорений.

Рівняння рівнозмінного руху:

x = + + ,

де – початкова координата точки, 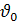– початкова швидкість.

Швидкість рівномірного руху:

𝜗 = + аt.

Пройдений шлях:

= + .

Виключивши час:

s = .

При рівномірному русі 𝜗 = соnst, а = 0.

Рівняння рівномірного руху:

x = + .

Існує два способи задання руху точки по криволінійній траєкторії.

За першим способом вказується траєкторія точки, а рівняння руху точки по кривій має загальний вигляд:

s = f(t).

При цьому величини середньої та миттєвої швидкостей визначаються таким способом, як і у випадку прямолінійного руху.

Напрям миттєвої швидкості в кожній точці траєкторії співпадає з напрямком дотичної до траєкторії в даній точці.

Для знаходження миттєвого прискорення його розкладають на дві складові: тангенціальну та нормальну.

Тангенціальне прискорення характеризує зміну швидкості за величиною, спрямоване по дотичній та визначається за формулою:

a _𝜏 = .

Нормальне прискорення характеризує зміну швидкості за напрямком, спрямоване до центра кривизни траєкторії та визначається за формулою:

a _n = ,

де R – радіус кривизни траєкторії.

Загальне прискорення:

a = .

Напрямок повного прискорення визначається кутами, які вектор прискорення утворює з радіусом або з дотичною. Косинуси цих кутів визначаються за формулами:

cos(а, а_n) = ;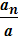

cos(а, а_𝜏 ) = .

При другому способі задання криволінійного руху вказується рівняння руху точки, що встановлює залежність координати точки від часу. Для випадку руху точки на площині достатньо задати два рівняння:

x = f₁(t);

y = f₂(t).

Проекції швидкостей на осі координат:

𝜗 _x = ;

𝜗 _y = .

Швидкість визначається через проекції за допомогою формули:

𝜗 = .

Напрямок швидкості визначається кутами, які вони утворюють з осями координат. Косинуси цих кутів визначаються за формулами:

cos(𝜗, 𝜗 _x) = 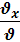; cos(𝜗, 𝜗 _y) = .

Проекції повного прискорення на осі координат:

a _x = ; a _y = .

Повне прискорення:

а = .

Напрямок повного прискорення визначається кутами, які вектор прискорення утворює з осями координат. Косинуси цих кутів визначаються за формулами:

cos(а, а_x) = , cos(а, а_y) = .

Будь-яка точка тіла, що обертається навколо осі, описує коло, площина якого перпендикулярна до осі обертання, а центр знаходиться на осі обертання.

Проведемо радіус-вектор такої точки в момент часу t = 0 і в будь-який інший момент часу t. Кут між цими двома положеннями радіус-вектора визначає кут повороту 𝜑 тіла. При обертанні тіла кут повороту 𝜑 є змінною величиною, що залежить від часу t.

Кінетичне рівняння обертального руху:

𝜑 = f (t).

Середня кутова швидкість:

𝜔 _с = ,

де 𝛥 𝜑 ― зміна кута повороту за час 𝛥 t.

Миттєва кутова швидкість:

𝜔 = .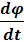

Середнє кутове прискорення:

𝛽 = ,

де 𝛥 𝜔 ― зміна кутової швидкості за час 𝛥 t.

Миттєве кутове прискорення:

𝛽 = = .

Рівняння рівнозмінного обертального руху:

𝜑 = + .

Кутова швидкість рівнозмінного обертального руху:

𝜔 = + 𝛽 t.

Кутове прискорення:

𝛽 = соnst.

Рівняння рівномірного обертання:

𝜑 = 𝜔 t.

При рівномірному обертанні кутова швидкість:

𝜔 = соnst.

Кутове прискорення: 𝛽 = 0.

Хід роботи

Приклад. Рівняння руху матеріальної точки вздовж осі має вид х = А + Вt + Ct³, де А = 2 м, В = 1 м/с, С = – 0, 5 м/с³. Знайти координату х, швидкість υ та прискорення а в момент часу t = 2 с.

Розв’язок. Координату х знайдемо, підставивши в рівняння руху числові значення коефіцієнтів А, В і С та часу t:

х = (2 + 1 × 2 – 0, 5 × 2³) м = 0.

Миттєва швидкість є перша похідна від координати за часом:

У момент часу t = 2 с.

υ = (1 – 3 × 0, 5 × 2²) м/с = – 5 м/с.

Прискорення точки знайдемо, взявши першу похідну від швидкості за часом:

У момент часу t = 2 с. а = 6 (– 0, 5) × 2 м/с² = – 6 м/с².

Задачі

Прямолінійний рівноприскорений рух

1. Рух тіла заданий рівнянням:

x = 3t 0, 25 .

Визначити момент часу, коли 𝛝 = 0. Знайти координату і прискорення в даний момент часу. Побудувати графік координати, шляху, швидкості даного руху.

2. Рух матеріальної точки заданий рівнянням:

x = 4t 0, 05 .

Визначити момент часу, коли 𝛝 = 0. Знайти координату і прискорення в даний момент часу. Побудувати графік координати, шляху, швидкості даного руху.

3. Дві матеріальні точки мають однакову початкову координату та напрямок руху. Друга точка почала свій рух через 2 с після початку руху першої. Перша точка рухалася з початковою швидкістю 1 м/с і прискоренням 2 м/ 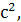друга – з початковою швидкістю 10 м/с і прискоренням 1 . Де і коли друга точка наздожене першу?

4. Рухи двох матеріальних точок задаються рівняннями:

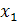= 20 + 2t 4 ;

= 2 + 2t + 0, 5 .

У який момент часу швидкості матеріальних точок будуть однаковими? Визначити швидкості та прискорення точок у цей момент часу.

5. Рухи двох матеріальних точок задаються рівняннями:

= 4t + 8 ;

= 2t .

У який момент часу прискорення матеріальних точок будуть однаковими? Визначити швидкості та прискорення точок в цей момент часу.

6. Рух точки по прямій задається рівнянням:

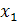=2t .

Визначити середню швидкість руху точки в інтервалі часу від t₁ =1 с до t₂= 3с.

7. Точка рухається по прямій згідно рівняння:

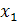=6t .

Визначити середню швидкість руху точки в інтервалі часу від t₁=2 с до t₂ =6 с.

8. Як напрямлене прискорен­ня кульки, що розхитується на нитці (див. рисунок), у точках А, В, С? Точка А — гранична точка траєкторії.

9. Точка рухається по кривій з постійним тангенціальним прискоренням 0, 5 м/с². Визначити повне прискорення точки на ділянці траєкторії з радіусом кривизни 3 м, якщо точка рухається із швидкістю 2 м/с.

10. Рух точки по траєкторії з радіусом кривизни 4 м заданий рівнянням:

= 10 t³ +5 .

Знайти тангенціальне, нормальне та повне прискорення точки в момент часу =2 с.

11. Рух точки по траєкторії з радіусом кривизни 4 м заданий рівнянням:

= 1 4t + t³.

Знайти тангенціальне, нормальне та повне прискорення точки в момент часу = 1 с.

12. Точка рухається по дузі кола, радіус якої становить 2 м згідно рівняння:

S = .

У який момент часу нормальне прискорення точки буде дорівнювати тангенціальному? Чому буде дорівнювати повне прискорення точки в даний момент часу?

13. Рух точки по прямій заданий рівнянням:

x = t³;

y = 2t.

Знайти рівняння траєкторії точки, її швидкість та прискорення в момент часу = 0, 8 с.

14. Диск радіусом 20 см, що знаходився в стані спокою, почав рухатися з постійним кутовим прискоренням 0, 5 рад/с². Визначити тангенціальне, нормальне та повне прискорення точок на колі диску через 2 с після початку обертання.

15. Диск радіусом 20 см обертається згідно рівняння:

= 4 4t + 0, 1 .

Визначити тангенціальне, нормальне та повне прискорення точок на колі диску в момент часу t=10с.

Питання для самоконтролю знань

1. Три способи визначення руху точки в просторі.

2. Швидкість руху точки. Миттєва та середня швидкість

3. Прискорення. Миттєве та середнє прискорення.

4. Рівнозмінний рух. Секторна швидкість і секторне прискорення.

5. Поступальний рух твердого тіла.

6. Обертальний рух твердого тіла навколо нерухомої осі.

7. Рівняння руху. Кутова швидкість тіла і кутове прискорення.