Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Данные / анализ данных / РЕГРЕССИЯ.
⇐ ПредыдущаяСтр 2 из 2
|
|
Коэффициенты а и b содержатся в столбце «коэффициенты».
| Коэффициенты | |
| Y-пересечение | a |
| t | b |
Опр. Коэффициент b называется выборочным коэффициентом регрессии. Величина коэффициента регрессии b показывает среднее изменение результата Y при увеличении фактора времени t на 1 единицу (с каждым годом, с каждым днем, …).
Смысл коэффициента a (значение Y в начальный момент времени) не представляет практического интереса.
Отчет о работе программы «РЕГРЕССИЯ» содержит несколько таблиц. Искомые коэффициенты находятся в третьей таблице:
| Коэффициенты | |
| Y-пересечение | 10, 467 |
| t | 0, 770 |
Таким образом,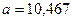 
; 
.
Уравнение модели имеет вид 
.
, следовательно, с каждым годом урожайность Y увеличивается в среднем на 0, 770 ц/га.
Для построения чертежа: правой кнопкой мыши кликнуть на графике исходных данных, выбрать меню добавить линию тренда, выбрать тип зависимости – линейный, параметры – показывать уравнение на диаграмме.
Получим:
После добавления линии тренда обязательно убедитесь, что коэффициенты, найденные программой Регрессия совпадают с теми, которые получены в уравнении на графике.
представляют собой случайную компоненту 
, следовательно, для них должны выполняться следующие свойства:
1. случайности;
2. равенства нулю математического ожидания;
3. независимости;
4. нормального распределения.
Таким образом, если все перечисленные свойства для остаточной компоненты выполняются, то можно говорить о том, что модель правильно отражает систематические компоненты временного ряда. Такая модель называется адекватной.
Вычислим значения остаточной компоненты 
и рассмотрим способы проверки адекватности и точности модели.
можно найти в столбце «Остатки» таблицы «ВЫВОД ОСТАТКА».
Для проверки случайности уровней ряда остатков используется критерий поворотных точек (пиков), в соответствии с которым:
1.Определить количество поворотных точек р: п оворотными являются точки экстремума (мин и макс) на графике остатков.
Выделим поворотные точки на графике: лев кнопкой мыши кликнуть на точке, кликнуть правой кнопкой, выбрать «Формат точки данных» и изменить маркер.
Подсчитаем их количество: 
.
вычисляют критическое значение, где квадратные скобки означают, что от результата вычисления в правой части необходимо взять целую часть
(не путать с процедурой округления!).
.
- если 
, то свойство случайности уровней ряда остатков выполняется;
- если 
, то ряд остатков нельзя считать случайным, он содержит регулярную компоненту, следовательно, модель не является адекватной.
> 
, следовательно, свойство случайности для ряда остатков выполняется.
выполняется автоматически; для других – требует проверки.
. Таким образом, проверка по критерию Стьюдента не требуется, проверяемое свойство выполняется.
.
2. По таблице d – статистик Дарбина – Уотсона определяют критические уровни: нижний d1 и верхний d2.
3. Сравнивают полученную фактическую величину d с критическими уровнями d1 и d2 и делают вывод согласно схеме:
- если 
, то уровни ряда остатков сильно автокоррелированы, модель неадекватна;
- если 
, то однозначного вывода о зависимости или независимости уровней ряда остатков по критерию Дарбина-Уотсона сделать нельзя, требуется дополнительная проверка;
- если 
, то уровни ряда остатков являются независимыми;
- если 
, то это свидетельствует об отрицательной корреляции. В этом случае перед проверкой величину d следует заменить на 
.
Дополнительную проверку свойства независимости ряда остатковвыполняют с помощью первого коэффициента автокорреляции.
1. Вычисляют первый коэффициент автокорреляции 
.
2. По таблице критических уровней корреляции определяют критическое значение 
.
3. Сравнивают полученную фактическую величину 
с критическим значением 
и делают вывод согласно схеме:
- если 
, то свойство независимости остаточной компоненты выполняется;
- если 
, то наблюдается существенная автокорреляция уровней ряда остатков, модель неадекватна.
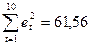(fx/математические/ СУММКВ)
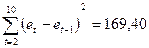(fx/математические/ СУММКВРАЗН).
Таким образом, 
.
Критические значения d – статистик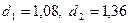 
заданы.
Согласно схеме проверки: 
.
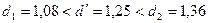. В этом случае на основании критерия Дарбина-Уотсона нельзя сделать однозначного вывода о зависимости или независимости остаточной компоненты. Требуется выполнить проверку свойства с помощью другого критерия.
Подготовим 
(fx/математические/ СУММПРОИЗВ).
Тогда 
.
Критическое значение для коэффициента автокорреляции задано 
.
Сравнение с критическим значением показывает, что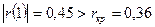 
. Таким образом, в ряде остатков наблюдается автокорреляция, свойство независимости остатков нарушается, модель не является адекватной и требует улучшения.
Дальнейшее рассмотрение этой модели проводим в учебных целях.
,
2. По таблице критических границ отношения R/S определяют критический интервал.
3. Сопоставляют фактическую величину R/S с критическим интервалом и делают вывод согласно схеме:
- если 
критическому интервалу, то гипотеза о нормальном распределении уровней ряда остатков принимается;
- если 
критическому интервалу, то уровни ряда остатков не подчиняются нормальному распределению, модель неадекватна.
Если все четыре свойства выполняются, делают вывод о том, что выбранная трендовая модель является адекватной реальному ряду наблюдений. Только в этом случае её можно использовать для построения прогнозных оценок. В противном случае модель нужно улучшать (изменить кривую роста, выделить дополнительные регулярные компоненты и т.п.).
(fx/статистические / МИН),
(fx/статистические / МАКС),
(fx/статистические / СТАНДОТКЛОН).
Вычислим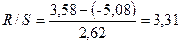 
.
При 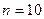критические уровни R/S – критерия 
.
, значит, для построенной модели свойство нормального распределения остаточной компоненты выполняется.
Проведенная в рассмотренном примере проверка свойств адекватности показывает, что построенная модель урожайности не является адекватной (для нее нарушается свойство независимости остаточной компоненты).
Дальнейшее рассмотрение этой модели проводим в учебных целях.
.
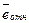Предварительно для всех уровней ряда остатков вычисляют относительные погрешности 
, затем определяют их среднюю величину .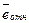
Вывод о точности модели делают согласно схеме:
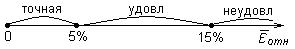Для сравнительной оценки точности различных моделей можно использовать среднее квадратичное отклонение ряда остатков 
.
В общем случае допустимый уровень точности устанавливает пользователь модели, который в результате содержательного анализа проблемы выясняет, насколько велики потери из-за неточного решения.
(fx/ математические / ABS), где ei - остаток на i -ом уровне, уi - соответствующее значение исходного значения Y.
Получим:
| Наблюдение | Предсказанное Y | Остатки | относ. погр |
| 11, 23636 | -0, 93636 | 9, 09 | |
| 12, 00606 | 2, 29394 | 16, 04 | |
| 12, 77576 | -5, 07576 | 65, 92 | |
| 13, 54545 | 2, 25455 | 14, 27 | |
| 14, 31515 | 0, 08485 | 0, 59 | |
| 15, 08485 | 1, 61515 | 9, 67 | |
| 15, 85455 | -0, 55455 | 3, 62 | |
| 16, 62424 | 3, 57576 | 17, 70 | |
| 17, 39394 | -0, 29394 | 1, 72 | |
| 18, 16364 | -2, 96364 | 19, 50 |
Средняя относительная погрешность аппроксимации составит
% (fx /статистические / СРЗНАЧ).
% > 15%. Следовательно, точность модели неудовлетворительная.
.
В случае линейной модели роста 
.
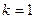, при этом 
.
Согласно уравнению модели получим точечную прогнозную оценку 
Таким образом, ожидаемое значение урожайности в будущем году составит около 18, 93 ц/га.
.
Затем рассчитывают границы интервала вокруг точечного прогнозного значения
и 
.
Размах u характеризует ошибку прогнозирования. Чем больше размах, тем менее точным является прогноз.
).
Для расчета подготовим:
(fx/статистические /СТЬЮДРАСПОБРпри
);
(найдено ранее);
(fx/статистические / СРЗНАЧ);
(fx/статистические / КВАДРОТКЛ).
По формуле вычислим размах прогнозного интервала:
Теперь можно определить границы:
и
Таким образом, с вероятностью 95% можно утверждать, что урожайность в будущем году будет от 11, 19 ц/га до 26, 68 ц/га.
Для наглядности покажем результаты расчета прогнозных оценок на графике: выбрать данные/добавить
· «точечный прогноз», 
, 
;
· «нижняя граница», , 
;
· «верхняя граница», , 
.
Большой размах прогнозного интервала говорит о низкой точности прогнозирования. Это объясняется низким качеством используемой модели.
.
Здесь k – период упреждения (количество шагов прогнозирования);
- расчетное значение показателя У для 
- периода;
- коэффициенты модели, изменяющиеся (адаптирующиеся) во времени.
По основной формуле Брауна производится расчет прогнозных значений показателя У на k шагов вперед.
Уточнение (корректировка) коэффициентов при переходе от уровня 
к новому моменту времени 
производится по формулам:
,
.
Здесь 
- ошибка прогноза, найденного по модели Брауна для момента t.
b - коэффициент дисконтирования данных, отражающий степень важности более поздних данных.
Для временного ряда урожайности построить модель Брауна (принять коэффициент сглаживания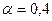 
) и рассчитать прогноз урожайности на 2 года вперед. Исходные данные, результаты моделирования и прогнозирования показать на чертеже.
В качестве значений 
используют коэффициенты вспомогательной линейной модели 
, построенной по первым пяти уровням ряда 
.
С помощью «Данные/ анализ данных/ РЕГРЕССИЯ» найдем
| Коэффициенты | |
| Y-пересечение | 9, 59 |
| Переменная t | 0, 97 |
Примем 
, 
, занесем эти значения в нулевой уровень соответствующих столбцов основной расчетной таблицы и перейдем к построению собственно модели Брауна. Согласно условию задачи коэффициент сглаживания 
.
| год | урож-ть | построение модели Брауна | |||
| t | Y(t) | a(t) | b(t) | Yp(t) | e(t) |
| 9, 59 | 0, 97 | ||||
| 10, 3 | 10, 4 | 0, 9 | 10, 6 | -0, 3 | |
| 14, 3 | 13, 2 | 1, 4 | 11, 3 | 3, 0 | |
| 7, 7 | 10, 2 | 0, 3 | 14, 6 | -6, 9 | |
| 15, 8 | 13, 9 | 1, 1 | 10, 5 | 5, 3 | |
| 14, 4 | 14, 6 | 1, 0 | 15, 0 | -0, 6 | |
| 16, 7 | 16, 3 | 1, 2 | 15, 7 | 1, 0 | |
| 15, 3 | 16, 1 | 0, 9 | 17, 5 | -2, 2 | |
| 20, 2 | 19, 0 | 1, 4 | 17, 0 | 3, 2 | |
| 17, 1 | 18, 3 | 0, 8 | 20, 4 | -3, 3 | |
| 15, 2 | 16, 6 | 0, 2 | 19, 1 | -3, 9 | |
| 16, 8 | |||||
| 17, 0 |
Таким образом, модель Брауна построена.