
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дослідні закони теплопровідності та внутрішнього тертя та їх мол.-кін. тлумачення
|
|
Внутрішнє тертя. Якщо швидкості впорядкованого руху молекул у потоці газу змінюються від шару до шару (тобто шари рухаються з різними швидкостями), то між шарами газу виникають сили
внутрішнього тертя (див. рис. 2.5), які визначаються за формулою


де η – коефіцієнт внутрішнього тертя,;
 – градієнт швидкості впорядкованого руху молекул, величина, яка характеризує зміну швидкості у перпендикулярному напрямку до вектора u;
– градієнт швидкості впорядкованого руху молекул, величина, яка характеризує зміну швидкості у перпендикулярному напрямку до вектора u;
S – площа шарів, які стикуються між собою.
Коефіцієнт внутрішнього тертя чисельно дорівнює силі, що діє на одиничну площадку при одиничному градієнті швидкості. Молекули газу переходять внаслідок теплового руху з шару в
шар і переносять з собою імпульс. У результаті імпульс більш повільного шару зростає, а більш швидкого зменшується. Перенесення імпульсу з шару в шар і обумовлює виникнення внутрішнього тертя.
У молекулярно-кінетичній теорії виводиться формула для коефіцієнта внутрішнього тертя  де ρ – густина газу; < v> – середня швидкість теплового руху молекул; λ – середня довжина вільного пробігу молекул.
де ρ – густина газу; < v> – середня швидкість теплового руху молекул; λ – середня довжина вільного пробігу молекул.
Теплопровідність. Якщо в газі вздовж деякого напрямку
z температура не залишається сталою, то вздовж цього напрямку
встановлюється потік q тепла в напрямку зменшення температури
(див. рис. 2.6).

де 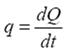 – потік теплоти, тобто кількість тепла, яка переноситься через площадку S у одиницю часу;
– потік теплоти, тобто кількість тепла, яка переноситься через площадку S у одиницю часу;  – градієнт температури, який характеризує швидкість зміни температури вздовж осі Z
– градієнт температури, який характеризує швидкість зміни температури вздовж осі Z
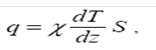 (2.22) де – коефіцієнт теплопровідності, cV, який дорівнює потоку тепла через одиничну площадку при одиничному градієнті температури; V c -питома теплоємність.
(2.22) де – коефіцієнт теплопровідності, cV, який дорівнює потоку тепла через одиничну площадку при одиничному градієнті температури; V c -питома теплоємність.
Теплопровідність обумовлена тим, що переміщуючись внаслідок теплового руху, кожна молекула переносить з місця з більшою температурою в місце з меншою температурою енергію < > = ikT /2. У результаті теплопровідності температура менш нагрітих місць підвищується, а температура більш нагрітих – зменшується. Коли температури вирівнюються, потік тепла припиняється.
16.Другий закон термодинаміки.(16.1)
Неможливі процеси, єдиним і кінцевим результатом яких був би перехід тепла від тіл менш нагрітих до тіл більш нагрітих.
Круговий процес ( цикл ) – процес, при якому система, проходячи через ряд станів, повертається в початковий стан.
Отже робота, що здійснюється газом за цикл, визначається площею, охоплюваною замкненою кривою. Якщо за цикл здійснюється позитивна робота A = ∫ pdV > 0 (протікає за год. стріл.), то його називають прямим (рис. 3.1, а), якщо за цикл здійснюється негативна робота A = ∫ pdV < 0 (проти г. с.), то його називають зворотнім (рис. 3.1, б). Прямий цикл використовують в теплових двигунах – двигунах, що діють періодично і виконують роботу за рахунок одержаної ззовні теплоти. Зворотній цикл використовують в холодильних машинах – установках, що діють також періодично, але в яких за рахунок роботи зовнішніх сил теплота переноситься до тіл з вищою температурою від менш нагрітих тіл.
У результаті кругового процесу система повертається в початковий стан і, таким чином, повна зміна внутрішньої енергії газу дорівнює нулю (dU = 0). Тому перший закон термодинаміки для кругового процесу Q =∆ U + A = A, тобто робота, що здійснюється за цикл, дорівнює кількості одержаної ззовні теплоти. Однак в результаті кругового процесу система може теплоту як одержувати, так і віддавати, тому Q = Q1 - Q2, де Q1 – кількість теплоти, одержана системою; Q2 – кількість теплоти, віддана системою.
Термодинамічний процес називають оборотним, якщо він може відбуватися як у прямому, так і у зворотному напрямі. Всякий процес, що не задовольняє цим умовам, є необоротним.
Поняття оборотного процесу можна віднести тільки до замкненої системи.
Звичайно, всі процеси в реальних системах необоротні. Якщо перейти до теплових процесів, то всі теплові процеси необоротні. Відомо, що теплообмін завжди походить від гарячого тіла до холодного, причому до тих пір, поки температури тіл не стануть однаковими.
У теплових двигунах використовується прямий цикл. Від нагрівача T1, за цикл віднімається кількість теплоти Q1, а холодильнику T2, за цикл передаєтьсякількість теплоти Q2, при цьому здійснюється робота А = Q1 – Q2.
(ККД): 
У холодильній машині (рис. 3.5, b) використовується зворотній цикл. За цикл системою від холодильника T2 віднімається кількість теплоти Q2 і віддається нагрівнику T1 кількість теплоти Q1. Для кругового процесу Q = А, але є умова Q = Q2 - Q1 < 0, тому А < 0 і Q2 - Q1 = - A.
Таким чином, без здійснення роботи не можна відбирати теплоту від менш нагрітого тіла і віддавати її більш нагрітому. Це твердження є не що інше, як другий закон термодинаміки у формулюванні Клаузіуса.
Цикл Карно. З другого закону термодинаміки випливає, що єдиним оборотним процесом, який супроводжується теплообміном з тепловим резервуаром з постійною температурою, є ізотермічний процес, що протікає при температурі резервуара. 
Отже оборотний цикл, у ході якого система вступає у теплообмін з двома тепловими резервуарами, повинен складатися з двох ізотерм і двох адіабат. Адіабати йдуть крутіше ізотерм і замикають дві ізотерми у цикл. Такий цикл було введено в розгляд Карно і він отримав його ім’я (див. рис. 2.3), а теплова машина, яка працює за циклом Карно, називається ідеальною тепловою машиною.
ККД циклу Карно визначається формулою  Справедливі два твердження:
Справедливі два твердження:
1. ККД всіх оборотних теплових машин, що працюють в ідентичних умовах (тобто при однакових температурах нагрівача і охолоджувача), однаковий.
 2. ККД теплової машини, яка працює за необоротним циклом, завжди менший, ніж ККД машини, що працює за оборотним циклом, якщо умови роботи двох машин однакові. Це пояснюється тим, що повна робота при необоротному циклі менша, ніж при оборотному.
2. ККД теплової машини, яка працює за необоротним циклом, завжди менший, ніж ККД машини, що працює за оборотним циклом, якщо умови роботи двох машин однакові. Це пояснюється тим, що повна робота при необоротному циклі менша, ніж при оборотному.
Ентропія. Із виразів ККД для циклу Карно (2.13), (2.14) випливає Таким чином, ентропія є мірою хаосу (невпорядкованості) в системі. Чим більша ентропія – тим більший хаос в системі. З урахуванням необоротних процесів формулу (2.16) переписуємо у вигляді нерівності  (2.18) де знак рівності береться для оборотних процесів, а нерівності – для необоротних. Для ізольованої системи D Q=0 і D S. 0. З цього випливає, що:
(2.18) де знак рівності береться для оборотних процесів, а нерівності – для необоротних. Для ізольованої системи D Q=0 і D S. 0. З цього випливає, що:
1) ентропія ізольованої системи тільки збільшується, якщо процеси в неї необоротні (закон збільшення ентропії);
2) ентропія ізольованої системи залишається сталою, якщо процеси в ній оборотні (закон збереження ентропії).
 Функцію стану, диференціалом якої є (3.2), називають ентропією і позначають S (таке поняття ентропії введене в 1865 р. Р. Клаузіусом).
Функцію стану, диференціалом якої є (3.2), називають ентропією і позначають S (таке поняття ентропії введене в 1865 р. Р. Клаузіусом).
Можна дати коротше формулювання другого закону термодинаміки: у процесах, що відбуваються в замкненій системі, ентропія не зменшується. Тут важливо, що йдеться про замкнені системи, оскільки в незамкнених системах ентропія може поводитися будь-яким чином (зменшуватися, зростати, залишатися постійною). Крім того, підкреслимо ще раз, що ентропія залишається постійною у замкненій системі тільки при оборотних процесах. При необоротних процесах у замкненій системі ентропія завжди зростає.
Формула Больцмана (3.12) дозволяє дати статистичне тлумачення другого закону термодинаміки. Постулат другого закону – зростанняентропії в замкненій системі при необоротних процесах, означає перехідсистеми з менш вірогідних у більш вірогідні стани.
Наведемо ще два формулювання другого закону термодинаміки:
1) за Кельвіном: не можливий круговий процес, єдиним результатом якого є перетворення теплоти, одержаної від нагрівача, в еквівалентну їй роботу;
2) за Клаузіусом: не можливий круговий процес, єдиним результатом якого є передача теплоти від менш нагрітого тіла до більш нагрітого.
З формулювання другого закону термодинаміки за Кельвіном виходить, що вічний двигун другого роду – діючий періодично двигун, який здійснює роботу за рахунок охолоджування одного джерела теплоти, – неможливий.
-------------------------------------------------------- 17 -------------------------------------------------------
17. Реальні гази.(17.1) Реа́ льний газ— газ, що не підлягає рівнянню стану ідеального газу Клапейрона-Менделєєва, молекули його взаємодіють між собою та займають певний об'єм.
17.3.Рівняння Ван-дер-Ваальса(17.2.Відступи від законів ідеальних газів)
Рівняння стану реального газу в загальному вигляді має вигляд f(p, V, Т )= 0, (5.2), де кожна із змінних є функцією двох інших. Взаємодія молекул реального газу обумовлює відхилення рівняння (5.2) від рівняння Менделеєва-Клапейрона, що описує ідеальний газ.
Голландський фізик Ван-дер-Ваальс у 1873 р. вивів рівняння стану реального газу, вводячи в рівняння Менделеєва-Клапейрона поправки на власний об'єм молекул і сили міжмолекулярної взаємодії.
1. Врахування власного об'єму молекул. Наявність сил відштовхування, які протидіють проникненню в зайнятий молекулою об'єм інших молекул, зводиться до того, що фактичний вільний об'єм, в якому можуть рухатися молекули 1 моля реального газу, буде не Vm, а Vm – b, де b – об'єм, займаний самими молекулами. Об'єм b дорівнює збільшеному вчетверо власному об ' єму молекул.
2. Облік притягання молекул. Дія сил притягання між молекулами газу приводить до появи додаткового тиску на газ, названого внутрішнім тиском. За обчисленнями Ван-дер-Ваальса, внутрішній тиск обернено пропорційний до квадрата молярного об'єму:  де а – постійна Ван-дер-Ваальса, що характеризує сили міжмолекулярного притягання; Vm – молярний об'єм. Вводячи обидві поправки і рівняння Менделеєва-Клапейрона, одержимо рівняння Ван - дер - Ваальса для 1 моля газу (рівняння стану
де а – постійна Ван-дер-Ваальса, що характеризує сили міжмолекулярного притягання; Vm – молярний об'єм. Вводячи обидві поправки і рівняння Менделеєва-Клапейрона, одержимо рівняння Ван - дер - Ваальса для 1 моля газу (рівняння стану
реальних газів): 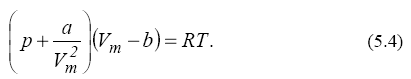 Для довільної кількості речовини ν газу рівняння Ван-дер-Ваальса
Для довільної кількості речовини ν газу рівняння Ван-дер-Ваальса
набуде вигляду  де поправки а і b – постійні для кожного газу величини, визначувані експериментально (записуються рівняння Ван-дер-Ваальса для двохвідомих з досліду станів газу і розв'язуються відносно а і b). Рівняння Ван-дер-Ваальса, зважаючи на цілий ряд спрощень, є наближеним і кількісно описує властивості реальних газів у області високих температур і низького тиску. Рівняння Ван-дер-Ваальса – не єдине
де поправки а і b – постійні для кожного газу величини, визначувані експериментально (записуються рівняння Ван-дер-Ваальса для двохвідомих з досліду станів газу і розв'язуються відносно а і b). Рівняння Ван-дер-Ваальса, зважаючи на цілий ряд спрощень, є наближеним і кількісно описує властивості реальних газів у області високих температур і низького тиску. Рівняння Ван-дер-Ваальса – не єдине
рівняння, що застосовується до опису реальних газів.