
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция задана таблично. Пользуясь интерполяционной формулой Ньютона, вычислить значение функции для аргумента .
|
|
Таблица 3 – Задание функции 

| 
| 
| 
| 
| 
| |||
| 0, 1 0, 2 0, 3 0, 4 0, 5 0, 6 | 1, 00000 1, 20500 1, 42007 1, 64538 1, 88124 2, 12815 2, 38676 | 0, 7 0, 8 0, 9 1, 0 1, 1 1, 2 1, 3 | 2, 65797 2, 94290 3, 24293 3, 55975 3, 89537 4, 25216 4, 63285 | 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | 5, 04065 5, 47918 5, 95261 6, 46561 7, 02350 7, 63219 8, 29835 | |||
Оценить погрешность вычислений, погрешность метода, суммарную погрешность, если точность входных данных одинакова  .
.
3. Функция  задана таблично. Вычислить значения функции с точностью ε = 10-3 с помощью интерполяционного многочлена Лагранжа. Оценить погрешность вычислений, погрешность метода, суммарную погрешность.
задана таблично. Вычислить значения функции с точностью ε = 10-3 с помощью интерполяционного многочлена Лагранжа. Оценить погрешность вычислений, погрешность метода, суммарную погрешность.
Таблица 4– Задание функции 
| 0, 00 | 0, 08000 | 0, 13000 | 0, 20000 | 0, 27000 | 0, 31000 | 0, 38000 | 0, 44000 |
| 1, 00000 | 1, 72539 | 1, 97664 | 1, 92950 | 1, 45474 | 1, 07307 | 0, 42687 | 0, 09338 |


4. С точностью ε = 10-3 найти наименьший положительный корень уравнения f(x) = 0 тремя способами
1. Методом половинного деления
2. Методом Ньютона
3. Методом хорд
(Номер выполняемого примера 4. n, где  ).
).
Результаты занести в таблицу. Сделать выводы.
 4.1.
4.1.
 4.2.
4.2. 
4.3.
5. Дана таблица значений функции  (см. пример 2). Вычислить значения
(см. пример 2). Вычислить значения 
 и
и  в заданных точках. Оценить погрешность вычислений, считая, что функция в таблице задана точно. Аргумент
в заданных точках. Оценить погрешность вычислений, считая, что функция в таблице задана точно. Аргумент  (не совпадает с узлами таблицы!)
(не совпадает с узлами таблицы!)
6. Вычислить определённый интеграл тремя способами с помощью формул:
· -трапеций;
· -Симпсона;
· -прямоугольников (3 шт.)
с числом узлов  для каждого метода.
для каждого метода.
Оценить погрешность вычислений интеграла по формуле Рунге. Выполняемый вариант – номер в списке группы по модулю 12.
1.  ; 2.
; 2.  ; 3.
; 3. 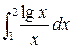 ; 4.
; 4.  ; 5.
; 5.  ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8.  ; 9.
; 9.  ; 10.
; 10. 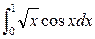 ; 11.
; 11.  ; 12.
; 12.  .
.
7. Вычислить интеграл по формуле Гаусса и оценить погрешность для числа узлов  . Выполняемый – номер в списке группы по модулю 3..
. Выполняемый – номер в списке группы по модулю 3..
1.  ; 2.
; 2.  , 3.
, 3.  .
.
8. Сравнить работу различных модификаций метода Ньютона для фиксированного  =6 нахождения корня функции, а именно:
=6 нахождения корня функции, а именно:
- модифицированный метод Ньютона;
- метод ложного положения;
- метод секущих;
- метод Стефенсена.
Результаты занести в таблицу. Функция в табл.2
| модифиц. метод Ньютона | метод ложного положения | метод секущих | метод Стефенсена | ||||||||

|

| число |

|

| число |

|

| число |

|

| число |
| верн. знач. | выч. функций | верн. знач. | выч. функций | верн. знач. | выч. функций | верн. знач. | выч. функций | ||||
9. Сравнить эффективность работы модификаций метода Ньютона для достижения необходимой точности:
- модифицированный метод Ньютона;
- метод ложного положения;
- метод секущих;
- метод Стефенсона.
Задаются: - ε = 0, 01, Функция в табл.2 Результаты занести в таблицу.
| .модифиц. метод Ньютона | метод ложного положения | метод секущих | метод Стефенсена | ||||||||

| 
| 
| 
| (ε  ) )
| 
| 
| (ε  ) )
| 
| 
| (ε  ) )
| |
10. .Сравнить работу методов Ньютона и обратной квадратичной интерполяции для фиксированного числа шагов.
Задаются: число узлов  =6; функция в табл.2. Результаты занести в таблицу.
=6; функция в табл.2. Результаты занести в таблицу.
| метод Ньютона | метод обратной квадратичной интерполяции | ||||

| 
| число ВЗЦ | 
| 
| число ВЗЦ |
11. Сравнить работу методов с высоким порядком сходимости для достижения заданной точности. ε = 0, 01
- метод Ньютона;
- метод секущих;
- метод Стефенсена
f(x) – функция в табл.2... Результаты занести в таблицу.
12. Сравнить эффективность метода Ньютона и метода обратной квадратичной интерполяции для достижения заданной точности. ε = 0, 01
: f(x – функция в табл.2. Результаты занести в таблицу.
13. Вычислить коэффициенты обусловленности корней полинома пятой степени в зависимости от коэффициентов полинома a priori и a posteori, то есть теоретически и вычислив корни полинома с помощью приближенных методов по формуле Ньютона. Покажите, что для кратных и простых корней метод имеет различную скорость сходимости
Коэффициенты уравнения вещественны и заданы с точностью 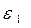 , которая должна быть предварительно подсчитана.
, которая должна быть предварительно подсчитана.
Ответ – 30 штук значений для коэффициентов обусловленности!!!!! Номер выполняемого варианта – номер в списке по модулю 11.
1. (х-2, 1114)3(х-1)(х-5)=0
2. (х+2)(х+1, 12459)(х-3)2(х-2.5)=0
3. (3х+2, 122345)(х+2)3(х-4)=0
4. (х+3)2(2х+3, 12987)(х-2)2=0
5. (х+2)3(х-1)(x-4.12654)=0
6. (2x-7.4445)4 (x+12)=0
7. (2х-1)3(х-1)(х-4.45689)=0
8. (2х-1)(х-1.6548)2(х-5)2=0
9. (х-1.32154)(х-4)2(х-5)2=0
10. (2х-1)(х-4)2(х-5.65321)2=0
11. (2х-1.25864)(х-1)2(х-4)2=0