
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычисление производных
|
|
Вычислить приближённые значения производных (первой и второй) для функции f (x), заданных в таблице 1. Аргумент задан в таблице.
Первую производную аппроксимировать центральным разностным отношением, а для второй производной использовать формулу
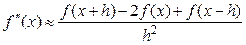
(а) Найдите приближения к первой производной по указанному правилу для всех трёх функций. Используйте формулу центрального разностного отношения для значений 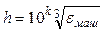 ,
,
где k = -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
(б) Вычислите приближения для вторых производных. Шаг тот же.
В каждом случае сравните вычисленные приближения с истинными значениями производных. Можете ли вы объяснить, как на выбор наилучшего значения h влияет поведение функции f (x) вблизи точки x?
(в) Используйте технику экстраполяции, чтобы улучшить приближения, полученные в пунктах (а) и (б).
(г) Сделайте выводы, проанализировав погрешность вычислений. Результаты оформите в таблице, сравнив точные и приближенные значения производных, а также полученную ошибку. Приведите график ошибки в зависимости от k.
ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ
Ниже приводится пример выполнения задания для указанного варианта.
| номер | Фамилия | 1, 14 | лабор. работа | ||||||||
| m | N функ. | x. | N примера | N примера | N примера | N функции | N примера | ||||
| 1, 1 |
1 Задание №1
Задание
Найти корни уравнения f(x) = 0 методом итераций с точностью ε =10-4.

1.2. Идея метода простых итераций
Представим функцию f(x)=0 в виде x = φ (x). На каждом шаге x(n) = φ (x(n-1)). Значение x(n) постепенно приближается к корню уравнения f(x)=0.
1.3. Построение итерационной функции
Преобразуем выражение 
 или
или  , значит,
, значит,
 – искомая итерационная функция
– искомая итерационная функция
1.4. Критерий окончания итерационного процесса
Требуемая точность будет достигнута, когда  , где q = max|φ ’(x)| на промежутке [0, 0.5].
, где q = max|φ ’(x)| на промежутке [0, 0.5].
Так как  на промежутке [0, 0.5], то q = φ ’(0) = 0.5
на промежутке [0, 0.5], то q = φ ’(0) = 0.5
Таблица 1 – Поиск корня уравнения методом простых итераций.
| Номер п/п, n | Предыдущее приближение, x(n-1) | Текущее приближение, x(n) |

|
| 0.0000 | 0.5000 | 1.0000 | |
| 0.5000 | 0.4196 | 0.1609 | |
| 0.4196 | 0.4437 | 0.0482 | |
| 0.4437 | 0.4369 | 0.0135 | |
| 0.4369 | 0.4389 | 0.0039 | |
| 0.4389 | 0.4383 | 0.0011 | |
| 0.4383 | 0.4385 | 0.0003 | |
| 0.4385 | 0.4384 | 0.0001 |
Вывод: С помощью метода простых итераций за 8 шагов был найден корень уравнения f(x)=0, полученный корень:
x = 0.4384±0.0001
2. Задание №3
2.1. Задание
Функция  задана таблично. Вычислить значения функции с помощью интерполяционного многочлена Лагранжа. Оценить погрешность вычислений, погрешность метода, суммарную погрешность.
задана таблично. Вычислить значения функции с помощью интерполяционного многочлена Лагранжа. Оценить погрешность вычислений, погрешность метода, суммарную погрешность.
Таблица 2 – Задание функции.
| 0, 00 | 0, 08000 | 0, 13000 | 0, 20000 | 0, 27000 | 0, 31000 | 0, 38000 | 0, 44000 |
| 1, 00000 | 1, 72539 | 1, 97664 | 1, 92950 | 1, 45474 | 1, 07307 | 0, 42687 | 0, 09338 |


2.2. Идея метода
Поскольку в таблице значение функции заданы с четырьмя знаками после запятой, выберем точность аргумента, которая не ухудшит точность входных данных x=0.1010192
В общем случае будем заменять функцию f(x) полиномом степени n
Pn(x) = a0 + a1× x + a2× x2 +... + an× xn
совпадающим с функцией f(x) в n+ 1 табличных точках xi, называемых узлами интерполяции
a0 + a1× xi + a2× xi2 +... + an× xin = f(xi), i =0, 1, 2 ,...n. (1)
Система уравнений (1) может быть решена, если среди узлов xi нет совпадающих. Используя решение этой системы интерполяционный полином можно записать в виде полинома Лагранжа
 // формула
// формула
В нашем случае будем интерполировать функцию полиномом Лагранжа 2 степени, для точек №1, 2 и 3.
2.3. Оценка погрешности метода
Ошибка приближения функции интерполяционным полиномом это разность Rn(x) = f(x) - Pn(x), где

Приближенно найдем третью производную функции, заменив полином Лагранжа третьей степени. Тогда третья производная постоянна и равна старшему члену полинома Лагранжа третьей степени, умноженному на 3!.
2.3. Оценка погрешности вычислений.
Пусть ε = 0.00001 – погрешность исходных данных, ……………..
//…надо сделать!!!!!!
2.4. Вывод.
С помощью метода интерполяции полиномами Лагранжа было получено приближенное значение функции в точке  .
.
f(x) = 1.859±0.005
3. Задание №4
3.1. Задание
С точностью ε = 10-3 найти наименьший положительный корень уравнения f(x) = 0.
1. Методом половинного деления
2. Методом Ньютона
3. Методом хорд
Результаты занести в таблицу. f(x) = tg(2x)+2x
a. Исследование задачи
Построив график функции f(x) (Рис. 1), находим, что наименьший положительный корень уравнения f(x)= 0 находится на промежутке
[0.8, 1.2]. Все методы будем применять для поиска корня именно на этом промежутке.
b. Идея метода половинного деления.
Разделим исходный отрезок [a, b] пополам c=(a+b)/2. Проверяя знаки f(a), f(b), f(c) выясним в каком из отрезков [a, c] или [c, b] содержится корень
x* Î [a, c], если f(a)f(c) < 0;
x* Î [c, b], если f(c)f(b) < 0.
Выбранный отрезок принимаем за [a, b] и повторяем это до тех пор, пока получаемый отрезок не сожмется до заданной степени точности.

Рисунок 3.1. График функции f(x)
c. Идея метода половинного деления.
Разделим исходный отрезок [a, b] пополам c=(a+b)/2.
Проверяя знаки f(a), f(b), f(c) выясним в каком из отрезков [a, c] или [c, b] содержится корень
x* Î [a, c], если f(a)f(c) < 0;
x* Î [c, b], если f(c)f(b) < 0.
Выбранный отрезок принимаем за [a, b] и повторяем это до тех пор пока получаемый отрезок не сожмется до заданной степени точности.
d. Идея метода Ньютона
Зададим некоторое начальное приближение x 0Î [a, b] и линеаризуем функцию f(x) в окрестности x0 с помощью отрезка ряда Тейлора
f(x) = f(x0) + f '(x0) (x-x0).
Решим линеаризованное уравнение f(x0) + f '(x0)(x-x0) = 0,
трактуя его решение x как первое приближение к корню
x1 = x0 - f(x0)/f '(x0).
Продолжая этот процесс, приходим к формуле Ньютона
 ,
,
которую можно считать итерационным процессом с итерирующей функцией s(x) = x - f(x)/f '(x).
e. Идея метода хорд
Этот метод можно получить из метода Ньютона, заменив производную f '(x) отношением разности функции к разности аргумента в окрестности рассматриваемой точки

Геометрически это означает, что приближенным значением корня считается точка пересечения секущей, проходящей через две точки функции f(x(n)) и f(x(n-1)), с осью абсцисс.
Таблица 3 – Нахождение корня уравнения методом половинного деления
| Число шагов, n | Начало промежутка, a | Конец промежутка, b | Длина промежутка, |a-b| |
| 0.800 | 1.200 | 0.400 | |
| 1.000 | 1.200 | 0.200 | |
| 1.000 | 1.100 | 0.100 | |
| 1.000 | 1.050 | 0.050 | |
| 1.000 | 1.025 | 0.025 | |
| 1.012 | 1.025 | 0.012 | |
| 1.012 | 1.018 | 0.006 | |
| 1.012 | 1.015 | 0.003 | |
| 1.014 | 1.015 | 0.001 | |
| 1.014 | 1.014 | 0.000 |
Таблица 4 – Нахождение корня уравнения методом Ньютона
| Число шагов, n | Текущее приближение, x(n) | Точность, |x(n)-x(n-1)| |
| 0.800 | - | |
| 0.814 | 0.014 | |
| 0.840 | 0.026 | |
| 0.883 | 0.043 | |
| 0.943 | 0.060 | |
| 0.995 | 0.052 | |
| 1.013 | 0.018 | |
| 1.014 | 0.001 | |
| 1.014 | 0.000 |
Таблица 5 – Нахождение корня уравнения методом хорд
| Число шагов, n | Текущее приближение, x(n) | Текущее приближение, x(n) |
| 1.183 | 0.017 | |
| 0.944 | 0.238 | |
| 1.053 | 0.108 | |
| 1.024 | 0.029 | |
| 1.013 | 0.011 | |
| 1.014 | 0.001 | |
| 1.014 | 0.000 |
Замечание Промежуточные вычисления ведем с запасными цифрами!! Здесь их нет!!!!
3.6. Вывод: Наименьший положительный корень уравнения f(x)=0 x = 1.014±0.001. С помощью метода половинного деления требуемой точности удалось достичь за 10 шагов, с помощью метода Ньютона – за 8 шагов, с помощью метода хорд – за 7 шагов. Значит, в нашем случае, наибольшей скоростью сходимости обладает метод хорд.
4. Задание №5
4.1. Задание
Дана таблица значений функции  . Вычислить значения
. Вычислить значения 
 и
и  в заданной точке x=1.1. Оценить погрешность вычислений, считая, что функция в таблице задана точно.
в заданной точке x=1.1. Оценить погрешность вычислений, считая, что функция в таблице задана точно.
Таблица 6 – Задание функции  .
.

| 
| 
| 
| 
| 
| |||
| 0, 1 0, 2 0, 3 0, 4 0, 5 0, 6 | 1, 00000 1, 20500 1, 42007 1, 64538 1, 88124 2, 12815 2, 38676 | 0, 7 0, 8 0, 9 1, 0 1, 1 1, 2 1, 3 | 2, 65797 2, 94290 3, 24293 3, 55975 3, 89537 4, 25216 4, 63285 | 1, 4 1, 5 1, 6 1, 7 1, 8 1, 9 2, 0 | 5, 04065 5, 47918 5, 95261 6, 46561 7, 02350 7, 63219 8, 29835 | |||
4.2. Метод решения задачи
Для вычисления первой производной в точке x воспользуемся центральным разностным соотношением:
 , где h = 0.1
, где h = 0.1
Для вычисления второй производной в точке x воспользуемся формулой
 , которая получается, если дважды применить формулу центрального разностного соотношения.
, которая получается, если дважды применить формулу центрального разностного соотношения.
4.3. Оценка погрешности вычислений
// Погрешность вычислений …………?????????? ……………
4.4. Вывод: первая и вторая производные в точке x=1.1 получились равными:
f’(1.1)≈ 3.4620499610900±0.0000000000001
f’’(1.1)≈ 2.117013931274±0.000000000001
5. Задание №6
5.1. Задание
Вычислить определённый интеграл с помощью формул:
-трапеций;
-Симпсона;
-прямоугольников (3 шт.) с числом узлов  .
.
Оценить погрешность по формуле Рунге.

5.2. Описание метода решения задачи
Для вычисления определенного интеграла воспользуемся так называемыми квадратурными формулами. Формула прямоугольников для приближенного вычисления определенного интеграла от непрерывной на [ a, b ] функции f(x) имеет вид:
 ,
,  ,
, 
//не копировать формулы!!!!!
Формула трапеций для приближенного вычисления определенного
интеграла от непрерывной на [ a, b ] функции f(x) имеет вид:
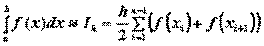 ,
,  ,
, 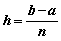
Формула Симпсона для приближенного вычисления определенного
интеграла от непрерывной на [ a, b ] функции имеет вид:
 ,
,  ,
, 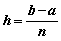 , n=2m.
, n=2m.
//не копировать!!!!!
5.3. Оценка погрешности квадратурных формул. Правило Рунге.
Для оценки погрешности R квадратурной формулы для непрерывной на
[ a, b ] функции f(x), можно использовать правило Рунге: вычислить по
соответствующей квадратурной формуле с шагом h=(b-a)/n и с шагом h/2
значения I k и I k/ 2, и найти приближенное значение интеграла и оценку
погрешности по формулам:
 ,
,  — для формулы прямоугольников;
— для формулы прямоугольников;
 ,
,  — для формулы трапеций;
— для формулы трапеций;
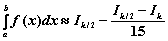 ,
,  — для формулы Симпсона.
— для формулы Симпсона.
Таблица 7 – Вычисление определенного интеграла с помощью квадратурных формул
| In (n = 12) | In/2 (n = 24) | I | R | |
| Формула трапеций | 0.5259 | 0.5294 | 0.5282 | 0.0012 |
| Формула Прямоугольников | 0.5158 | 0.5257 | 0.5291 | 0.0033 |
| Формула Симпсона | 0.5293 | 0.5305 | 0.5304 | 0.0001 |
5.4. Вывод: искомый определенный интеграл у меня получился равным:
I ≈ 0.528±0.002 – по формуле трапеций
I ≈ 0.529±0.004 – по формуле прямоугольников
I ≈ 0.5304±0.0001 – по формуле Симпсона
Как видно, наименее точной из этих формул является формула прямоугольников, наиболее точной – формула Симпсона.
6. Задание №7
6.1. Задание
Вычислить интеграл по формуле Гаусса и оценить погрешность для  :
:

6.2. Описание метода решения задачи
Воспользуемся следующей формулой: 
Где ti – нули полинома Лежандра 4 степени P4(x)=1/8(35x4-30x2+3)
Коэффициенты Ai и точки ti –табличные величины.//!!!!
6.3. Оценка погрешности
Остаточный член формулы Гаусса для n =4 выражается следующим образом:
 .
.
// далее: ищем!!! Десятую производную и её максимум!!!!!! *
…………………………………………………………
6.4. Вывод: искомый интеграл получился равным:
I ≈ 0.20067069544±0.00000000003
Данный метод оказался очень точным.
7. Задание №12
7.1. Задание
Сравнить эффективность метода Ньютона и метода обратной квадратичной интерполяции для достижения заданной точности. ε = 10-4.
f(x) = x2 – cos π x на промежутке [0, 0.5]
7.2. Описание метода решения задачи
Метод Ньютона для поиска корней уравнения был описан выше (см. пункт 3.4)
Метод обратной квадратичной интерполяции заключается в следующем:
Выбираем любые три точки на промежутке [a, b], и находим по ним уравнение параболы x = g(y). На каждом шаге находим следующее приближение:
x(n) = g(0)
Продолжаем этот процесс, пока |x(n)-x(n-1)|> =ε
Таблица 8 – Сравнение эффективности метода Ньютона и метода обратной квадратичной интерполяции
| Метод Ньютона | Метод обратной квадратичной интерполяции | ||
| n | x(n) | n | x |
| 0.2000 | 0.4400 | ||
| 0.5423 | 0.4384 | ||
| 0.4407 | 0.4384 | ||
| 0.4384 |
7.3. Вывод: Метод обратной квадратичной интерполяции оказался более эффективным, чем метод Ньютона. Скорость сходимости этих методов примерно одинакова, однако метод Ньютона обладает локальной сходимостью, а метод обратной квадратичной интерполяции более стабилен.
8. Задание №13
8.1. Задание
Вычислить коэффициенты обусловленности корней полинома пятой степени в зависимости от коэффициентов полинома a priori и a posteori, то есть теоретически и вычислив корни полинома с помощью приближенных методов по формуле Ньютона. Покажите, что для кратных и простых корней метод имеет различную скорость сходимости
Коэффициенты уравнения вещественны и заданы с точностью ε м, которая должна быть предварительно подсчитана.
(2х-1)(х-4)2(х-5)2=0
8.2. Алгоритм определения машинной точности
float em = 0.5;
while (em + 1. > 1.)
{
em = em/2.;
}
em = em*2.;
Если использовать компилятор, входящий в пакет Microsoft Visual Studio 6.0, машинная точность получается примерно равной ε m≈ 0.000000000000000222.
// привести характеристики PC
8.3. Априорная оценка погрешности
Вычислим корни уравнения. Они равны:
x1 = 0.5 – корень первой кратности
x2, 3 = 4 – корень второй кратности
x4, 5 = 5 – корень второй кратности
Сначала найдем коэффициенты обусловленности для корня первой кратности.
Раскроем в уравнении скобки и получим:
2x5-37x4+260x3-841x2+1160x-400
Рассмотрим неявно заданную функцию:
φ (xk, a0, a1, a2, a3, a4, a5)=  , где:
, где:
xk – один из корней уравнения;
a0, a1, a2, a3, a4, a5 –коэффициенты уравнения.
Тогда i -ый корень будет определяться через коэффициенты: xi=φ (a0, a1, a2, a3, a4, a5)
Погрешность функции многих переменных определяем по формуле:  , где:
, где:
ν i – коэффициент обусловленности;
δ ai – относительная погрешность коэффициента (она равна машинной точности).
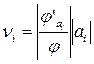
Найдем производную неявной функции  :
:
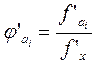


Тогда:
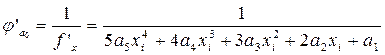





Найдем коэффициенты обусловленности для корня x1 = 0.5:
// привести явную формулу для вычисления коэффициентов!!!!
ν 0 = 1.612
ν 1 = 2.338
ν 2 = 0.848
ν 3 = 0.131
ν 4 = 0.009
ν 5 = 0.000
Таким образом, x1 ≈ 0.5000000000000000±0.0000000000000005
Теперь найдем коэффициенты обусловленности для корней второй кратности.
Для кратных корней (в нашем случае кратности 2) x1=x2=4 и x4=x5=5 коэффициент обусловленности будет стремиться к бесконечности, так как эти корни будут простыми корнями уравнения f’x=0.
Как и делалось выше, найдем обусловленность кратных корней x1=x2=4 и x4=x5=5. Необходимо отметить, что погрешность входных данных теперь 2ε м, так как коэффициенты представляют собой произведения первоначальных коэффициентов и степеней, которые ранее были представлены с точностью ε м.
Рассмотрим неявную функцию:
F(xi, a0, a1, a2, a3, a4)=a4xi4+a3xi3+a2xi2+a1xi+a0
F(xi, a0, a1, a2, a3, a4)=0
где:
a4=10
a3=-148
a2=780
a1=-1682
a0=1160
коэффициенты уравнения, а xi является одним из корней уравнения. Тогда i -ый корень будет определяться через коэффициенты: xi=φ (a0, a1, a2, a3, a4).
Погрешность функции можно определить по формуле:
 , где:
, где:
// считаем сами………………………………
………………………………………
8.4. Определение корней при помощи метода Ньютона
Идея данного метода описана в пункте 3.4.
Таблица 9 – Определение корней при помощи метода Ньютона
| Точное значение корня | Начальное приближение | Приближенное значение корня | Число итераций | Фактическая погрешность |
| 0.5 | 0.0 | 0.5000000000000000 | 0.0000000000000000 | |
| 3.5 | 3.9999997 | 0.0000003 | ||
| 5.5 | 5.0000004 | 0.0000004 |
// теперь нужно еще раз найти коэффициенты обусловленности, имея корни……….
8.5. Вывод: с помощью метода Ньютона корень первой кратности удалось вычислить точнее, чем при теоретической оценке. Корни второй кратности, наоборот, оказались менее точными. Так же было показано, что для корней первой и второй кратности метод Ньютона имеет обладает разной скоростью сходимости (в случае корней второй кратности сходится значительно медленнее).
// плохой вывод……
9. Задание №14
9.1. Задание
Вычислить приближённые значения производных (первой и второй) для функции
f (x) = x2 – cos π x в точке x = 0.26
Первую производную будем аппроксимировать центральным разностным отношением, а для второй производной используем формулу 
(а) Найдите приближение к первой производной по указанному правилу. Используйте формулу центрального разностного отношения для значений  , где k = -10, -9, -2, -1, 0, 1, 2, 9, 10.
, где k = -10, -9, -2, -1, 0, 1, 2, 9, 10.
(б) Вычислите приближение для второй производной. Шаг тот же.
В каждом случае сравните вычисленные приближения с истинными значениями производных. Можете ли вы объяснить, как на выбор наилучшего значения h влияет поведение функции f (x) вблизи точки x?
(в) Используйте технику экстраполяции, чтобы улучшить приближения, полученные в пунктах (а) и (б).
(г) Сделайте выводы, проанализировав погрешность вычислений. Результаты оформите в таблице, сравнив точные и приближенные значения производных, а также полученную ошибку
9.2. Описание метода решения задачи
Для вычисления первой производной в точке x воспользуемся центральным разностным соотношением:
 , где
, где  , k = -10, -9, …….. -2, -1, 0, 1, 2, 9, 10.
, k = -10, -9, …….. -2, -1, 0, 1, 2, 9, 10.
Для вычисления второй производной в точке x воспользуемся формулой
 ,
,
которая получается, если дважды применить формулу центрального разностного соотношения.
Таблица 10 – Приближенное вычисление производной
| k | h | f’(x) | Точное значение | Δ f’(x) | f’’(x) | Точное значение | Δ f’’(x) |
| -10 | 0.000000000000000606 | 15077840.000 | 2.81012 | 0.000 | 8.75621 | 8.756 | |
| -9 | 0.00000000000000606 | 1507784.000 | 1507781.25 | 0.000 | 8.756 | ||
| …….. | |||||||
| 6055.45 | 0.51 | 2.29 | 2.00 | 6.76 | |||
| 60554.54 | 0.51 | 2.29 | 2.00 | 6.76 |
// не все значения взяты!!!
9.3. Вывод: при приближенном вычислении производной с различным шагом наибольшая погрешность была получена при наименьшем шаге. Это связано с большой погрешностью вычислений. С увеличением шага погрешность сначала уменьшается (преобладает вычислительная погрешность, которая уменьшается с увеличением шага), затем достигает оптимального значения, и вновь начинает расти (преобладает методическая погрешность, которая растет с увеличением шага).
Список использованной литературы
1. Ю.П. Боглаев – Вычислительная математика и программирование
2. Б.П. Демидович, И.А. Марон – Основы вычислительной математики