Технологические методы обеспечения надежности

ТЕОРИЯ НАДЕЖНОСТИ

Методические указания к практической работе №1

«Статистическая оценка закона распределения времени безотказной работы по результатам определительных испытаний»

Составители:

д.т.н., профессор Богданович В.И.

к.т.н., доцент Плотников А.Н.

Самара 2013

Цель работы: изучение методики выравнивания эмпирических распределений, статической оценки правдоподобия гипотез и оценка технического совершенства изделия с позиции показателей надежности.

Введение

Возникающие отказы технических объектов и отклонения параметров качества при их изготовлении определяются случайными неблагоприятными сочетаниями многих факторов. Случайность заключается в том, что невозможно точно указать момент возникновения события или получаемое значение параметра.

Например, рассеяние ресурсов по критерию усталости, оцениваемое отношением наибольшего ресурса к наименьшему достигает 40. Значительным является рассеяние ресурсов по износу и коррозии. При выполнении любой технологической операции также возникает рассеяние параметров качества изделий.

Поэтому в расчетах на надежность многие параметры рассматриваются как случайные величины. Они могут быть непрерывного так и дискретного типа.

В математической теории надежности решаются в основном две задачи. Первая, вероятностная, заключающаяся в том, чтобы по известным функциям распределения вероятности наступления событий вычислить нужные показатели надежности и дать прогноз выполнения задания. Вторая задача называется статистической и заключается в том, что по результатам функционирования технических систем проводится оценка показателей надежности.

При решении второй задачи надежности, в зависимости от конкретных технических систем и целей, используются следующие методы:

1. расчетный;

2. опытно-статистический;

3. регистрационный;

4. экспертный.

1 Теоретические основы

Пусть технический объект начинает работу в момент времени , а в момент времени происходит его отказ.

Отказ – это случайное событие, поэтому при испытании различных однотипных систем время наступления отказа 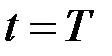будет различным.

Следовательно, время 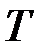– наработка до отказа является случайной величиной.

Множество возможных значений , называемое генеральной совокупностью, совпадает с множеством действительных чисел .

При проведении испытаний мы можем испытать только некоторое конечное число объектов . При этом получается конечный набор чисел . Этот конечный набор называется выборкой из генеральной совокупности, а число объемом выборки. Очевидно, что если мы возьмем других элементов и опять проведем испытания, то получим выборку, состоящую из других значений .

Поэтому все числовые характеристики, полученные из выборки, также являются случайными. Они называются статистическими и служат лишь для оценки вероятностей.

Рассмотрим методику обработки статистических данных для определения закона распределения наработки до отказа.

Возьмем выборку из не восстанавливаемых объектов. Запустим их в работу. Пусть за время отказали все объекты. В результате мы получим набор чисел . Проводим упорядочение этого набора, то есть все значения располагаем в порядке их возрастания. Полученный упорядоченный ряд носит название вариационного ряда.

Этот вариационный ряд описывает полную группу событий (отказов) поставленных на испытание изделий. В связи с тем, что из опытных данных, а также из чисто интуитивных соображений, все значения различны, поэтому можно считать, что любых два или более события не могут появиться вместе или одновременно. Такие события называются несовместимыми. По условиям симметрии испытаний у нас нет оснований считать, что какое-то из этих событий является более возможным, чем какое-то из этих событий является более возможным, чем любое другое. Такие события называются равновозможными.

В общем случае, вероятность некоторого события А для случая, когда события составляют полную группу, являются несовместимыми и равновозможными при независимых испытаний, оценивается как отношение числа случаев, благоприятных появлению данного события, к общему числу случаев, то есть даётся соотношением

, (1)

где – число случаев, благоприятных событию A, – общее число случаев.

В нашем примере эмпирическая (или статистическая) оценка вероятности (1) (также называемая частотой или частотностью наступления события) будет для всех событий наступления отказов в моменты времени одинакова и равна

, (2)

так число случаев благоприятных отказу в момент равно одному.

Таким образом, нашему испытанию объектов можно поставить в соответствие формализованное математическое описание, заключающееся в представлении результатов испытания рядом распределения случайной величины в виде таблицы 1.

Таблица 1 – Ряд распределения

			…
			…

В верхней строке Таблицы 1 перечислены в порядке возрастания все возможные значения случайной величины , а в нижней – статистические вероятности наступления этих событий.

В теории вероятности для описания случайных величин, множество возможных реализаций которых может принимать дискретное или непрерывное число значений на конечном или бесконечном интервале, вводится понятие функции распределения вероятностей (ФРВ) случайной величины.

По определению ФРВ некоторой случайной величины , имеющей область возможных значений реализации детерминированный интервал , называется функцией 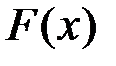, значения которой равны вероятности того, что случайная величина принимает значение меньшее, чем значение детерминированной величины 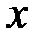, т.е.

. (3)

В рассматриваемом случае, когда случайная величина является наработкой до отказа , а область возможных реализаций представлена (в общем случае) бесконечным временным интервалом , соотношение (3) для ФРВ наработок до отказа (ФРВ отказов) должно быть записано в виде:

. (4)

Из определения ФРВ следует, что для таблицы 1 эмпирическая (или статистическая) ФРВ отказов принимает значения

. (5)

Следовательно, эмпирическая ФРВ отказов в нашем случае представляет собой ступенчатую функцию (рисунок 1), равную нулю при 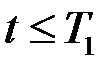и единице . Внутри этого интервала ФРВ непрерывна слева в точках , а справа в этой точке претерпевает скачок величиной и имеет скачков на этом интервале.

Рисунок 1 – Функция распределения вероятностей для таблицы 1

При неограниченном увеличении скачки станут все более мелкими, а сама она будет приближаться (сходиться по вероятности) к непрерывной функции распределения случайной величины .

Для практического использования более удобными являются группированный статистический ряд и гистограмма.

Для построения группированного статистического ряда отрезок разбивается на участков или разрядов. Для определения числа разрядов можно пользоваться приближенной формулой . При этом величина временного интервала составит (таблица 2). Величину или границы интервалов удобно брать в виде «круглых» чисел. Подсчёт числа попаданий случайной величины в интервал приводим во второй строке таблицы 2. При этом если значение случайной величины попало в точности на границу интервала, то его делят поровну между этими соседними интервалами, прибавляя по к числам для обоих соседних интервалов. Частоты или статистические вероятности для каждого интервала определяем в соответствии (1) по соотношению:

. (6)

Причём при этом естественно будет выполняться условие нормировки статистических вероятностей:

. (7)

Полученная часть таблицы 2, состоящая из трёх рассмотренных строк, носит название группированного статистического ряда. Разделив каждое значение на длину интервала , получим значения плотностей распределения статистической вероятности на каждом интервале:

. (8)

Эти значения записываем в четвёртой строке таблицы 2. Откладывая по оси абсцисс значения полученных интервалов и строя на каждом интервале как на основании прямоугольник площадью или высотой , получим гистограмму плотности распределения эмпирического числа отказов (рисунок 2).

Таблица 2 – Построение группированного статистического ряда, статистической плотности распределения, функции распределения вероятностей и интенсивности отказов

	Интервал разбиения			…		…	k
				…		…
				…		…
				…		…
				…		…
				…		…

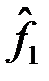
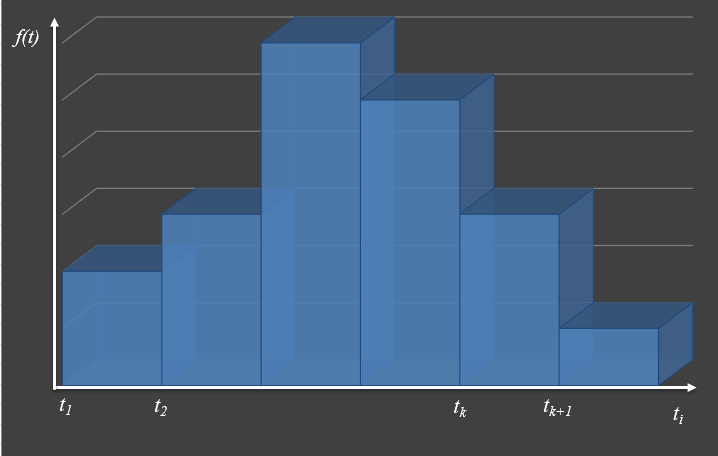
Рисунок 2 – Гистограмма плотности распределения вероятности наработок до отказа

Имея в своём распоряжении данные таблицы 2, строим статистическую функцию распределения вероятности отказов, значения которой на интервалах разбиения в соответствии с (4) рассчитываются по соотношению:

. (9)

Значения приводим в пятой строке таблицы 2. При построения гистограммы учитываем, что при значениях равна нулю, а при значениях единице.

В шестой строке таблицы 2 приводим значения интенсивности отказов для каждого интервала разбиения, значения которых определяем по соотношению:

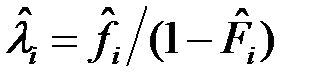. (10)

Интенсивность отказов определяется как условная плотность ФРВ отказов невосстанавливаемого изделия, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не наступил. Следовательно, интенсивность отказов также, как и плотность распределения , является дифференциальной характеристикой распределения, учитывающей только возможность возникновения отказа в рассматриваемый момент времени, без учёта предыстории функционирования изделия, в том смысле, что не учитывает отказы, которые могли бы произойти в предыдущие моменты времени.

Следующим этапом исследования является выравнивание статистического распределения. Во всяком статистическом распределении присутствуют элементы случайности, обусловленные ограниченностью числа опытов. Задача выравнивания заключается в выборе аналитической формулы, отражающей лишь существенные, наиболее характерные черты статистического материала.

Задача оптимального выбора выравнивающей кривой является в значительной мере неопределенной и не имеет строгого математического решения. Здесь приходится руководствоваться соображениями физики решаемой задачи, характером эмпирической зависимости, оценкой степени точности результатов наблюдений и т.д. Например, гистограмма, показанная на рисунке 2, явно наводит на мысль о нормальном распределении. Монотонное же убывание свидетельствовало бы о показательном распределении, как наиболее вероятном.

В любом случае наше суждение о законе распределения в принципе является предположением – гипотезой. Для ответа на вопрос о совместимости между выдвигаемой гипотезой и результатами наблюдений используются критерии согласия, наиболее употребительным среди которых является критерий (хи-квадрат) Пирсона (К.Э. Пирсон англ. статистик). В качестве меры расхождения между гипотетическим и эмпирическим распределениями используется величина , где – эмпирические вероятности (частоты), а – гипотетические вероятности попадания случайной величины в -й интервал.

Величина представляет собой взвешенную сумму квадратов разностей между гипотетическими и наблюденными частностями попадания случайной величины в -й интервал:

. (11)

Как доказал Пирсон, величина с возрастанием стремится к табличному распределению . Число степеней свободы связано с числом разрядов соотношением , где – число связей, наложенных на , 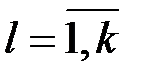(обычно ).

Алгоритм оценки правдоподобия гипотезы по критерию сводится к следующему.

1.1. В дополнение к группированному ряду по гипотетической плотности распределения вычисляются гипотетические интервальные вероятности:

. (12)

1.2 Вычисляется величина

1.3 По таблице распределения находится вероятность (приложение Б).

1.4 Если найденная вероятность достаточно мала (стандартные уровни значимост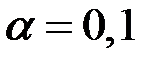и ; ), то выдвинутую гипотезу следует отвергнуть, как малоправдоподобную. В противном случае принять, как неопровергаемую результатами наблюдений.