Функция распределения вероятности случайных событий и отказов. Числовые характеристики функции распределения

При многократных наблюдениях за случайными событиями выявляется, что они подчиняются определенным закономерностям. Эти закономерности описываются законами теории вероятности. Случайная величина может быть непрерывной (время, длина и т.д.) или принимать дискретные значения (число отказов). Из-за невозможности заранее указать, какое конкретное значение примет случайная величина, для её характеристики вводится понятие вероятности.

Вероятность – это численная мера объективно существующей возможности появления (или непоявления) изучаемого события А, которая обычно обозначается через .

Классический способ определения вероятности основан на рассмотрении равновозможных событий, являющихся исходами данного испытания. В случае, когда такие испытания независимы, а события несовместны и образуют полную группу, вероятность события оценивается как отношение числа случаев, благоприятных появлению данного события, к общему числу событий. Эта эмпирическая (или статистическая) оценка вероятности получила название частота или частость случайного события. Частота равна отношению числа испытаний n, в которых появилось данное событие, к общему числу испытаний N.

. (1)

Величина частости сама является случайной величиной (в отличие от вероятности), так как в различных сериях испытаний её величина будет изменяться случайным образом, группируясь около своей вероятности. Отличие вероятности от её статистической оценки отмечено различным обозначением этих величин. Правомерность оценки вероятности частотой появления события вытекает из теоремы Бернулли, которая утверждает, что с вероятностью, как угодно близкой к достоверности, при достаточно большом числе испытаний N частота появления события, имеющего во всех испытаниях постоянную вероятность 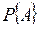, будет как угодно мало отличаться от этой вероятности:

.

Из определения вероятности следует, что 0£ £ 1. Событие, вероятность которого =1, называется достоверным, а событие, вероятность которого =0, называется невозможным.

Если случайное событие А заключается в том, что случайная величина x может принимать конечное (более двух) или бесконечное число значений, то для её характеристики необходимо использовать функцию распределения вероятности (ФРВ) случайной величины.

По определению ФРВ некоторой случайной величины x, имеющей область возможных значений реализации этой величины интервал [ a_н, a_в ], называется вероятность того, что случайная величина x принимает значения меньше, чем значение некоторой детерминированной величины х, т.е.

. (2)

Все множество возможных реализаций случайной величины x называется генеральной совокупностью, верхняя а_в и нижняя а_н границы которого для различных случайных величин могут принимать различные значения.

Из определения ФРВ видно, что она является функцией аргумента х, который является детерминированной переменной (в отличие от ξ) и поэтому к ФРВ применимы все хорошо известные математические методы.

По определению ФРВ обладает следующими свойствами: 1. является неубывающей функцией аргумента; 2. =0; 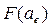=1. Последнее свойство носит название условие нормировки ФРВ.

Если задан некоторый интервал 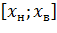, то вероятность обнаружения случайной величины ξ на интервале 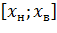определяется очевидным соотношением:

. (3)

Например, пусть какое-нибудь изделие начинает работать в момент времени t=0, а в некоторый момент времени t = Т возникает случайное событие - отказ изделия. Тогда множество возможных реализаций этих событий характеризуется количественно множеством значений, которое может принимать случайная величина, которую в этом случае принято обозначать не через x, а через Т. Это множество (генеральная совокупность) имеет границы a_н =0, a_в =+ ¥. В теории надежности величина Т получила название наработка до отказа, а ФРВ функции распределения вероятности наработок до отказа или просто «функции отказов»:

. (4)

В надежности часто необходимо оперировать не с ФРВ, которая по сути характеризует распределение отказов, а с обратной функцией, характеризующей ФРВ безотказной работы :

. (5)

Функцию распределения вероятности безотказной работы (5) для сокращения будем называть просто функцией надёжности.

Статистической оценкой вероятности наступления отказа в интервале от t=0 до t=k D t будет величина:

,

где - частота или статистическая оценка вероятности наступления отказа на некотором k -ом интервале ; - число изделий, отказавших на k -ом интервале; N – полное число изделий, поставленный на испытание и отказавших в результате этих испытаний.

Из определения следует, что F (0)=0и F (¥)=l, а сама функция F (t)является монотонной неубывающей функцией в этой области.

Аналогично вводится ФРВ при рассмотрении других случайных величин. Например, при выполнении технологического процесса получена партия одинаковых деталей, каждая из которых может быть охарактеризована некоторыми параметрами качества: геометрическими размерами, твердостью материала, пределом прочности и т.д. или отклонением этих параметров от заданного значения. При измерении этого параметра на одной из деталей мы получим его некоторое значение х. Очевидно, что при проведении следующего измерения на этой же детали (если это возможно) измеренное значение этого же параметра будет иметь другое значение. Кроме того, значение этого же параметра на другой детали из этой партии тоже будет иметь значение отличное от уже полученного. Следовательно, величина этого параметра качества является случайной величиной, которую для удобства обозначим через x. Все множество возможных реализаций этой случайной величины, в зависимости от ее конкретного физического смысла, может иметь верхнюю и нижнюю границы в виде конечных значений, в том числе и отрицательных (отклонение параметра от заданного значения). Часто, в определенных случаях значения этих границ, для удобства расчетов, не ограничивают конечными значениями, а продолжают до -¥ или +¥. Такое искусственное расширение области реализации в каждом конкретном случае должно иметь должное количественное обоснование. В этом случае, как следует из определения , она принимает значения F(a_н)=0 и F(a_в)=1 и является монотонной неубывающей функцией в этой области.

В практических расчетах на надежность с помощью специальной процедуры стараются всегда перейти от значений, представляющих в этой области кусочно-непрерывную и ступенчатую функцию к непрерывной функции , которую также называют теоретической функцией распределения вероятности конкретной случайной величины. Это связано с тем, что несмотря на большое разнообразие технических изделий, а следовательно бесконечное множество экспериментальных распределений, все они сводятся к небольшому числу теоретических распределений.

Дифференциальной характеристикой ФРВ отказов является плотность и интенсивность отказов:

, , (6)

а их статистической оценкой являются величины:

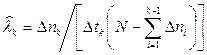и . (7)

Зная плотность распределения 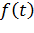из (6) легко найти интегрированием и , что с учётом даёт

где в этих соотношениях «неявную» переменную интегрирования t мы переобозначали через τ, чтобы её обозначение отличалось от переменной, стоящей в границах интегрирования.

Интенсивность отказов l(t) определяется как условная плотность ФРВ отказов невосстанавливаемого изделия, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не наступил. Следовательно, интенсивность отказов является дифференциальной характеристикой, учитывающей только возможность возникновения отказа в рассматриваемый момент времени, без учета предыстории функционирования изделия, в том смысле, что не учитывает отказы, которые произошли в предыдущие моменты времени.

Закон распределения случайной величины, представляемый в виде ФРВ этой случайной величины полностью описывает случайную величину с вероятностной точки зрения. Однако во многих практических вопросах нет надобности в таком полном описании, а достаточно бывает указать только некоторые отдельные численные параметры, характеризующие существенные черты распределения. Основными числовыми характеристиками ФРВ являются: математическое ожидание, дисперсия, коэффициент вариации и квантиль.

Математическое ожидание непрерывной случайной величины Т, имеющей ФРВ (4), определяется одним из следующих соотношений:

. (8)

Дисперсия непрерывной случайной величины характеризует её рассеивание вокруг математического ожидания и определяется следующими выражениями:

. (9)

В практических расчетах часто вместо дисперсии используют стандартное отклонение s_Т, имеющее ту же размерность, что и случайная величина. Стандартное отклонение равно . Рассеивание случайной величины вокруг её математического ожидания в относительных единицах (долях математического ожидания) характеризуется коэффициентом вариации: .

Квантиль порядка a случайной величины, имеющей ФРВ F(t), это такое значение случайной величины, при котором функция распределения этой величины принимает значение, равное a, т.е. квантиль t_a является корнем уравнения:

. (10)

Квантиль порядка a =0, 5 называется медианой распределения, так как делит площадь под графиком функции плотности распределения пополам, модой случайной величины является такое значение квантиля, которое соответствует максимальной величине плотности распределения.

Аналогично приводятся все приведенные выше определения для любой другой случайной величины x, а не только для наработки до отказа Т. При этом в приведенных формулах параметр t необходимо заменить на x, а в формулах (8) и (9) интегрирование проводить от нижнего (а_н)до верхнего (а_в) значения границы области возможной реализации случайной величины x.