Пример 3

.

Замечание. Из рассмотренных примеров видно, что предел частного двух многочленов при равен отношению коэффициентов при старших членах, если степени многочленов, стоящих в числителе и знаменателе, равны; равен нулю, если степень числителя меньше степени знаменателя; равен ¥, если степень числителя больше степени знаменателя.

3.2. Раскрытие неопределенности вида

Рассмотрим отношение функций 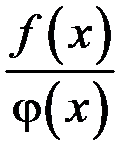. Пусть – бесконечно малые функции (б.м.ф.) при , отношение в этом случае называется неопределенным выражением вида .

Чтобы раскрыть неопределенность вида , заданную отношением двух многочленов, надо в числителе и знаменателе выделить критический множитель и сократить на него.

Чтобы раскрыть неопределенность вида , в которой числитель или знаменатель содержит иррациональность, следует избавиться от иррациональности, домножив числитель и знаменатель на сопряженное выражение.

Пример

Вычислить предел .

Решение

При числитель и знаменатель дроби стремится к нулю, т.е. имеет место неопределенность вида . Для раскрытия неопределенности числитель и знаменатель дроби умножим на сопряженное знаменателю выражение, т.е. на сумму , а квадратный трехчлен разложим на множители, найдя для этого его корни:

,

тогда,

.

Таким образом, получим:

.