Классификация точек разрыва

Определение. Если в точке функция имеет пределы слева и справа и они равны между собой, а в точке

или функция не определена, то точка называется точкой устранимого разрыва функции .

В этом случае функцию можно доопределить в точке так, чтобы она стала непрерывной, т.е. положить

.

Определение. Если в точке функция имеет конечные пределы слева и справа, причем , то точка называется точкой разрыва функции 1-го рода.

При переходе через точку значение функции претерпевает скачок, измеряемый разностью .

Определение. Точка называется точкой разрыва 2-го рода, если в этой точке хотя бы один из пределов (справа или слева) не существует или равен .

Пример

В точках и 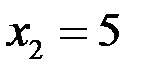для функции установить характер точек разрыва.

Решение

Область определения функции . Данная функция непрерывна во всех точках, кроме точек и 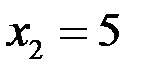, которые не входят в область определения функции.

Исследуем точку , находя ее односторонние пределы в этой точке:

если , то , тогда предел слева ,

если , то , тогда предел справа .

Так как односторонние пределы конечны, но не равны между собой, то в точке функция имеет разрыв 1-го рода (скачок функции).

Исследуем точку , находя ее односторонние пределы в этой точке:

если , то , тогда ,

если , то , тогда .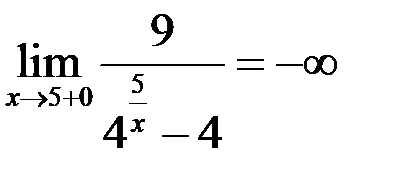

Так как односторонние пределы равны , то в точке функция имеет разрыв 2-го рода.