Пример 1.

Найти интеграл .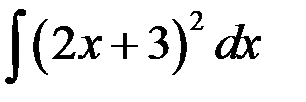

Так как 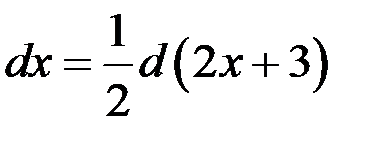, то

.

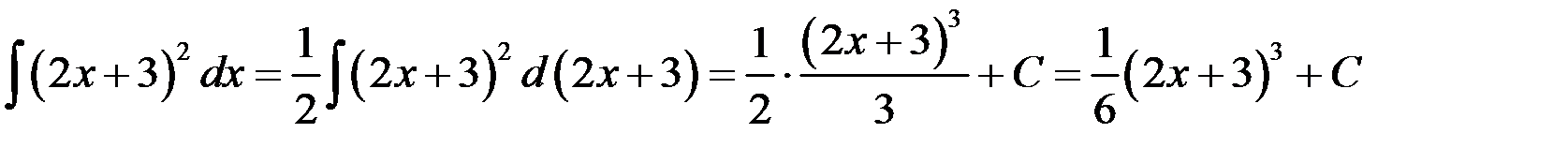Пример 2

Найти интеграл .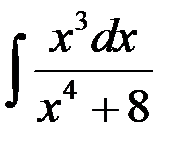

Так как 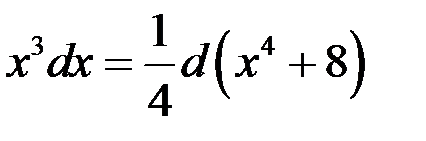, то

.

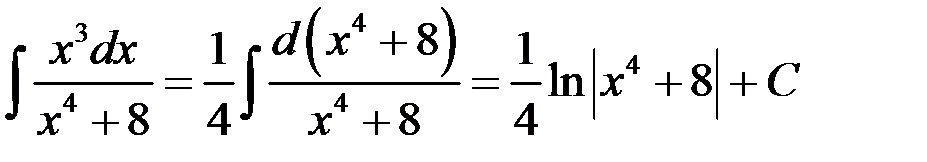Пример 3

Найти интеграл .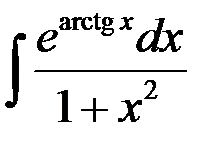

Так как 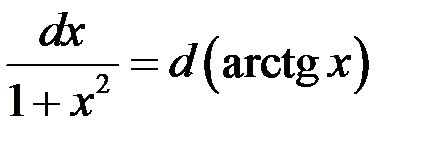, то

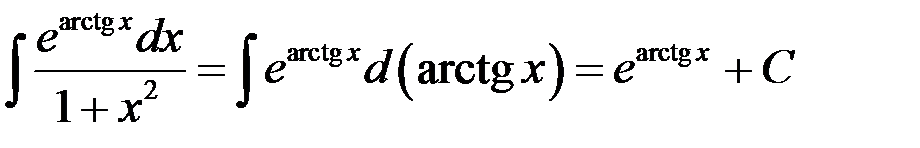
Пример 4

Найти интеграл .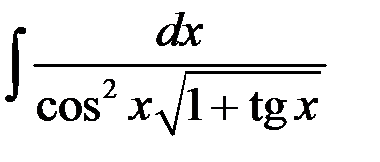

Так как 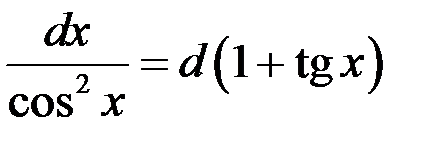, то

.

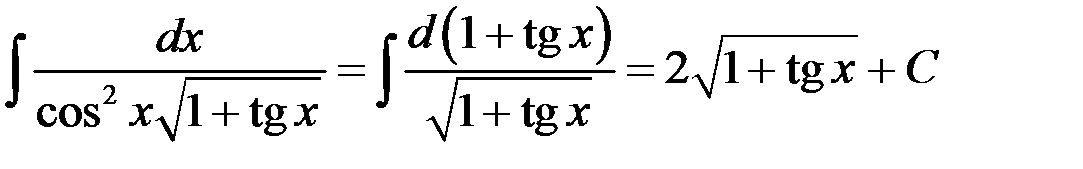Метод интегрирования по частям

Пусть дан интеграл вида 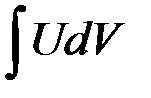, где 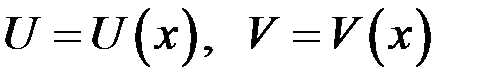- непрерывно дифференцируемые функции. Справедлива формула интегрирования по частям

.

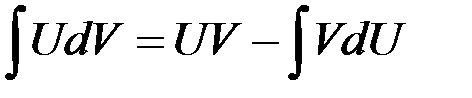Таким образом, вычисление интеграла 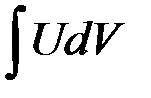приводится к вычислению интеграла 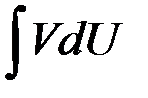, который может оказаться более простым или табличным.

Пусть 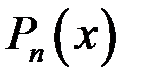- многочлен степени n. Методом интегрирования по частям можно вычислить, например, интегралы вида:

1 группа:	2 группа:

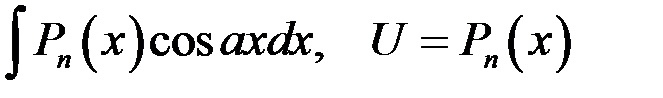
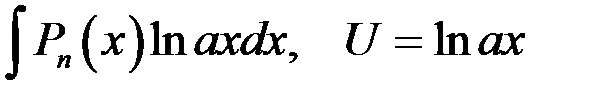
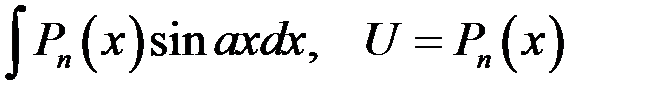
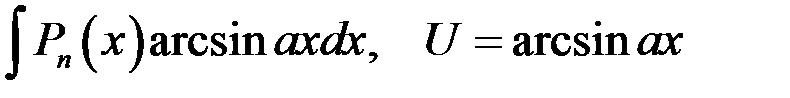
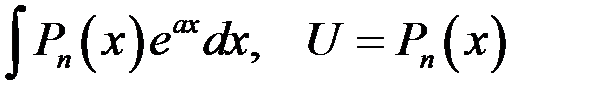
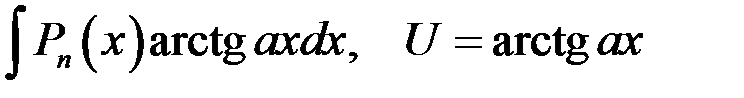
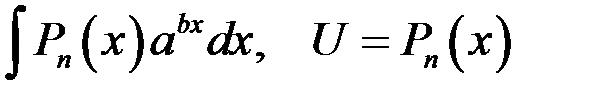
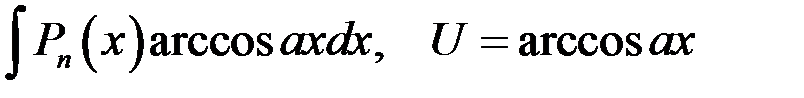
Пример

Найти интеграл .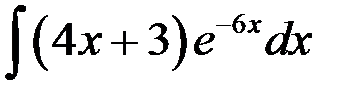

Решение

Положим 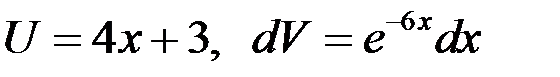, найдем 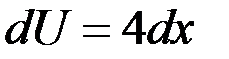, 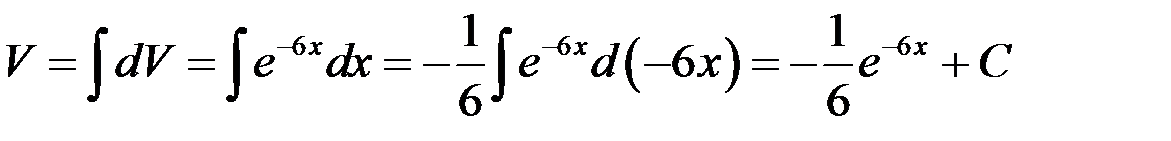. Так как достаточно взять одну из первообразных, то принимаем 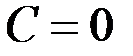. Применим формулу интегрирования по частям

.
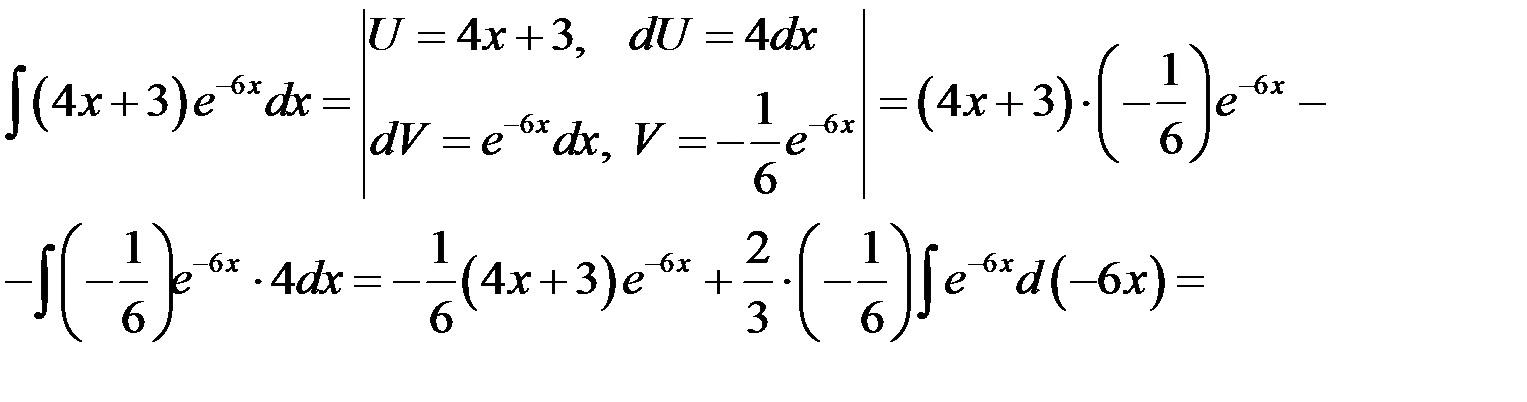
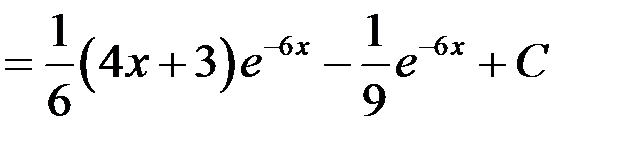