Задача № 7.

Определить отрывающее и сдвигающее усилия и полную силу давления жидкости на полусферическую крышку радиуса R, если заданы пьезометрический напор воды Н над центром крышки и угол наклона стенки бака к горизонту (рис. 7).

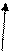
Рис. 7

Дано: Решение:

H = 1, 4 м; Используем уравнение равновесия жидкости, заполняющей

R = 0, 4 м; полусферическую крышку. На объем жидкости, находящейся в

α = 60^o полусфере, действуют:

G_x – вес жидкости выделенного объема (полусфера);

Найти: R_Fx – сила давления жидкости по плоскости круглого отверствия

Р_отр -? радиусом R;

Р_сдв -? R_х – сила реакций полусферической крышки;

R_Fx -? проектируя эти силы на ось х, имеем:

∑ х = R_Fx + G_x·cosα - R_х = 0;

следовательно:

R_х = R_Fx + G_x·cosα;

G_x = 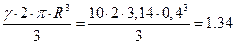кН;

R_Fx = γ ·Н·π ·R² =10·1, 4·3, 14·0, 4² = 7, 03 кН;

где γ =10 кН/м³;

тогда:

Р_отр = R_х = 7, 03 + 1, 34·cos60^o = 7.7 кН;

проектируя силы на ось у, имеем:

∑ у = G_x·sinα – R_y = 0;

P_сдв = R_y = 1.34·sin60^o = 1.16 к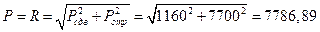Н;

Н;

Ответ: Р_отр = 7.7 кН; P_сдв = 1.16 кН; P = 7, 79 кН.