
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычисление параметров уравнения регрессии;
|
|
Для построения уравнения линейной регрессии и нахождения искомых параметров используют метод наименьших квадратов.
Сущность этого метода заключается в нахождении такой прямой, ординаты точек которой максимально приближенных к исходным (фактическим) значениям переменных. С помощью этого метода минимизируют расстояния по вертикали всех точек поля корреляции от этой прямой.
Этот метод позволяет получить такие оценки параметров модели, при которых сумма квадратов отклонений фактических значений зависимой переменной у от теоретических будетминимальна, т. е.
 min,
min,
где 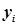 - исходные (фактические) значения зависимой переменной;
- исходные (фактические) значения зависимой переменной;
 - выравненные (расчётные) значения.
- выравненные (расчётные) значения.
Исходя из применения метода наименьших квадратов для вычисления параметров уравнения парной регрессии используют следующие формулы:

Коэффициент b при факторной переменной x имеет следующую интерпретацию: он показывает, на сколько единиц изменится в среднем величина y при изменении фактора x на 1 единицу измерения.

Параметр а может и не иметь экономического содержания. Интерпретируют знак при параметре а: если 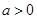 , то относительное изменение зависимой переменной происходит медленнее, чем изменение независимой переменной.
, то относительное изменение зависимой переменной происходит медленнее, чем изменение независимой переменной.