Уровень 1. Вычислить

a)

119. Уровень 2. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Вычислите ее скорость в момент времени t=3с.

a) 21км/ч

120. Уровень 2. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Вычислите ее скорость в момент времени t=4с.

a) 32 м/с

121. Уровень 2. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Вычислите ее ускорение в момент времени t=3с.

b) 10 м/с2

122. Уровень 2. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Вычислите ее скорость в момент времени t=5с.

a) 20 м/с

123. Уровень 2. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Вычислите ее ускорение в момент времени t=4с.

c) 7 м/с2

124. Уровень 2. Скорость точки, движущейся прямолинейно, задана уравнением V(t)=2t2-5t+6. В какой момент времени ускорение точки будет равно 2м/c2?

a) 1, 75 с

125. Уровень 2. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Вычислите ее скорость в момент времени t=5с.

a) 5 м/с

126. Уровень 2. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Вычислите ее ускорение в момент времени t=3с.

a) 2 м/с2

127. Уровень 2. Зависимость пути от времени при прямолинейном движении тел задана уравнениями:

.

В какой момент времени скорости их движения будут равными?

b) 1с

128. Уровень 2. Зависимость пути от времени при прямолинейном движении тел задана уравнениями:

.

В какой момент времени скорости их движения будут равными?

a) 4 с

129. Уровень 1. Найти производную функции у=4х3+0, 5х2+3 при данном значении аргумента, х=-1

a) 11

130. Уровень 1. Найти производную функции при данном значении аргумента, х=-2

a) 20

131. Уровень 1. Найти производную функции у=2х3+3х2+x-0, 7 при данном значении аргумента, х=1

a) 7

132. Уровень 1. Найти производную функции у=-2х3-1, 5х2-12 при данном значении аргумента, х=0

d) 0

133. Уровень 1. Найти производную функции у=х3-2, 5х2+x-25 при данном значении аргумента, х=-1

c) -13

134. Уровень 1. Найти производную функции при данном значении аргумента, х=2

a) -4

135. Уровень 1. Найти производную функции у=8х²-12х-13 при данном значении аргумента, х=-4

b) -76

136. Уровень 1. Найти производную функции у=-2х⁴+х³-x²-10 при данном значении аргумента, х=1

b) -7

137. Уровень 1. Найти производную функции у=4х3+0, 5х2+3 при данном значении аргумента, х=0

c) 0

138. Уровень 1. Найти производную функции при данном значении аргумента, х=0

e) 0

139. Уровень 1. Найти производную функции при данном значении аргумента, х=1

d) 16

140. Уровень 1. Найти производную функции у=-3х3+2х2-16 при данном значении аргумента, х=2

e) -28

141. Уровень 1. Найти производную функции у=4х3+0, 5х2+3 при данном значении аргумента, х=-3

a) 105

142. Уровень 1. Найти производную функции 8х²-12х-13 при данном значении аргумента, х=-1

a) -28

143. Уровень 1. Найти производную функции у=-4х²-3, 5х-100 при данном значении аргумента, х=-2

a) 12, 5

144. Уровень 1. Вычислить интеграл.

145. Уровень 1. Вычислить интеграл.

146. Уровень 1. Вычислить интеграл.

147. Уровень 1. Вычислить интеграл.

148. Уровень 1. Вычислить интеграл.

149. Уровень 1. Вычислить интеграл.

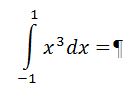
1/2

150. Уровень 1. Вычислить интеграл.

151. Уровень 1. Вычислить интеграл.

242/5

152. Уровень 1. Вычислить интеграл.

242/5

153. Уровень 1. Вычислить интеграл.

-5

154. Уровень 1. Вычислить интеграл.

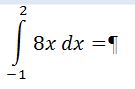
155. Уровень 1. Вычислить интеграл.

156. Уровень 1. Вычислить интеграл.

157. Уровень 1. Вычислить интеграл.

-7/2

158. Уровень 1. Вычислить интеграл.

-1/2

159. Уровень 2. Вычислить интеграл.

160. Уровень 2. Вычислить интеграл.

161. Уровень 2. Вычислить интеграл.

-7

162. Уровень 2. Вычислить интеграл.

163. Уровень 2. Вычислить интеграл.

164. Уровень 2. Вычислить интеграл.

a) 32/3

165. Уровень 2. Вычислить интеграл.

166. Уровень 2. Вычислить интеграл.

a) 104/3

167. Уровень 2. Вычислить интеграл.

a) 257/3

168. Уровень 2. Вычислить интеграл.

169. Уровень 2. Даны две точки: А(-3; 1; -1) и В(2; -4; 1). Вычислить координаты 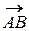и его длину.

a) (5; -5; 2)

d)

170. Уровень 2. Даны две точки: А(4; 0; 5) и В(3; 2; -1). Вычислить координаты 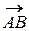и его длину.

a) (-1; 2; -6)

d)

171. Уровень 2. Даны две точки: А(-7; 0; -1) и В(-2; -5; 0). Вычислить координаты 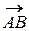и его длину.

a) (5; -5; 1)

c)

172. Уровень 2. Даны координаты точек А(0; -1; 2), В(-1; 4; 3), С(-2; 1; 0) и D(-1; 0; 3). Вычислите координаты вектора

a) (2; -6; 2)

173. Уровень 2. Даны координаты точек А(10; -3; 2), В(-1; 4; 5), С(-2; 4; 0) и D(-1; 0; 3). Вычислите координаты вектора

a) (12; -11; 0)

174. Уровень 2. Даны координаты точек А(0; -1; 2), В(-5; 0; 3), С(-7; 1; 0) и D(-1; 0; 9). Вычислите координаты вектора

a) (11; -2; 8)

175. Уровень 2. Вычислите скалярное произведение векторов , если

176. Уровень 2. Вычислите скалярное произведение векторов , если

177. Уровень 2. Вычислите скалярное произведение векторов , если

178. Уровень 2. Даны точки А(2; -3; 1) и В(1; 4; 0). Вычислить координаты 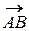и его длину.

a)

179. Уровень 2. Даны точки А(1; 0; -2), В(0; 3; 7), С(0; -3; 5), D(-1; 6; 0). Вычислите координаты вектора

a) (0; 6; -14)

180. Уровень 2. Даны точки А(-1; 2; 2), В(4; 2; 2), С(-4; -2; 2), D(1; -7; 2). Вычислите координаты вектора .

a) (0; -5; 0)

181. Уровень 1. В прямом параллелепипеде ребра, выходящие из одной вершины, равны 2, 3, 4 м, причем два больших образуют угол 30°. Вычислить объем параллелепипеда.

182. Уровень 1. Перекладина длиной 5 м прикреплена к стойкам на высоте 4 м от земли к одной и к другой на высоте 7 м. Определить расстояние между стойками.

183. Уровень 1. Стороны основания прямого параллелепипеда 6 и 4 см, острый угол в основании равен 30°. Найдите объем параллелепипеда, если высота его равна 7 см.

184. Уровень 1. В прямом параллелепипеде стороны основания равны 3 см и 5см и образуют угол в 30°; боковое ребро равно 7 см. Найти объем параллелепипеда.

52, 5

185. Уровень 1. В прямом параллелепипеде ребра, выходящие из одной вершины, равны 5, 6, 8м, причем два меньших образуют угол 30°. Вычислить объем параллелепипеда.

186. Уровень 1. Перекладина длиной 10 м прикреплена к стойкам на высоте 13 м от земли к одной и к другой на высоте 19 м. Определить расстояние между стойками.

187. Уровень 1. Стороны основания прямого параллелепипеда 8 и 2 см, острый угол в основании равен 30°. Найдите объем параллелепипеда, если высота его равна 7 см.

188. Уровень 1. В прямом параллелепипеде стороны основания равны 4 см и 7 см и образуют угол в 30°; боковое ребро равно 5 см. Найти объем параллелепипеда.

189. Уровень 1. В прямом параллелепипеде ребра, выходящие из одной вершины, равны 10, 6, 4 м, причем два меньших образуют угол 30°. Вычислить объем параллелепипеда.

190. Уровень 1. Перекладина длиной 13 м прикреплена к стойкам на высоте 16 м от земли к одной и к другой на высоте 28 м. Определить расстояние между стойками.

191. Уровень 2. 64 одинаковых шариков диаметром 4 см сплавили в один шар. Определить диаметр получившегося шара.

192. Уровень 2. Какое число шариков диаметром 2 см необходимо, чтобы перелить в них свинцовый шар диаметром 20 см.?

193. Уровень 2. Диаметры двух шаров соответственно равны 24 и 12 см. Во сколько раз объем одного из них больше объема другого?

a) 8

194. Уровень 2. Расстояние между двумя параллельными плоскостями равно 4 см. Отрезок длиной 5см своими концами упирается в эти плоскости. Определить проекции отрезка на каждую плоскость.

195. Уровень 2. Из некоторой точки A проведен к плоскости  перпендикуляр АО = 8 см и наклонная АС = 10 см. Найти проекцию наклонной AC на плоскость .

196. Уровень 2. Основание пирамиды – прямоугольник со сторонами 6 и 8 см. Каждое ребро пирамиды равно 13 см. Вычислить объем пирамиды.

a) 192 см3

197. Уровень 2. Внешний диаметр шара 16 см, толщина стенок 3 см. Найти объем стенок.

a) 516п см3

198. Уровень 2. Сторона основания правильной треугольной призмы равна 2 см, а боковое ребро 9см. Найти объем призмы.

a)

199. Уровень 2. Диагональ прямоугольного параллелепипеда составляет с плоскостью его основания угол 45°.Стороны основания равны 3 см. и 4 см. Найти объем.

a) 60 см3

200. Уровень 2. Высота прямого кругового конуса равна4 см., диаметр основания 6см. Найдите объём конуса.

b) 12п см2