Относительный покой.

Жидкость, заключенная в неподвижный резервуар и находящаяся в равновесии под действием силы тяжести, пребывает в абсолютном покое относительно земли.

Жидкость может быть в равновесии и при действии, помимо собственного веса, других сил, в том числе и сил инерции. Жидкое тело в таком случае будет находиться в относительном покое. Следует при этом иметь в виду, что жидкость начавшая двигаться из состояния абсолютного покоя приходит в состояние относительного покоя не сразу. Переход из одного состояния в другое происходит под влиянием сил трения; в самом состоянии относительного покоя силы трения отсутствуют. В качестве примера рассмотрим равновесие жидкости в двигающейся с постоянным ускорением цистерне, в которой действует объемная сила инерции, она направлена в противоположную сторону движения.

Выбрав подвижную систему координат с началом в точке пересечения свободной поверхности жидкости с передней стенкой цистерны и подставив в уравнение

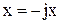, , Y=0, Z=-g (где jx- горизонтальное ускорение при движении) получим

Тогда, поделив обе части выражения на , для поверхности равного давления получим , или , то есть свободная поверхность в вагоне при равноускоренном движении представляет собой плоскость, наклонную под углом α к горизонтали.

Жидкость, заключенная в открытый сверху цилиндрический сосуд, вращающийся с постоянной угловой скоростью ω находиться в покое относительно сосуда. Для решения вопроса о форме поверхности жидкости в этом случае выберем начало координат в точке пересечения свободной поверхности жидкости с осью сосуда.

Тогда проекции ускорений на координатные оси , , подставляя в

(1)

Для начала координат, лежащего на оси вращения на свободной поверхности, координаты х=0, у=0, z=0. Следовательно, постоянная интегрирования поскольку , где r-расстояние от оси до рассматриваемой точки получим из (1)

Тогда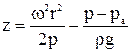

Для свободной поверхности жидкости манометрическое давление и ее уравнение примет вид .

Таким образом, в рассматриваемом случае свободная поверхность жидкости представляет собой парабалоид вращения.

Рассмотрим еще один случай когда жидкость находится в покое относительно резервуара, движущегося с постоянным ускорением j по наклонной плоскости, образующей с горизонтом угол α.

При этом Y=0. Подставим эти значения в получим

.

Отнеся обе части выражения к ρ установим, что поверхности равного давления, в том числе и свободная поверхность жидкости (dp=0), представляют собой семейство параллельных плоскостей, наклоненных к горизонту под углом

Если резервуар движется с постоянной скоростью то угол и поверхности равного давления представляют собой горизонтальные плоскости. Если резервуар движется только под действием силы тяжести (сила трения резервуара о плоскость равна нулю), то

, β =α, то есть поверхности равного давления образуют семейство плоскостей, параллельных плоскости скатывания.