Основное уравнение гидростатики.

Воспользуемся дифференциальным уравнением равновесия

Соблюдение условия равновесия требует при этом, чтобы и правая часть уравнения была

(1)

полным дифференциалом некоторой другой функции координат 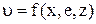, частные производные которой по координатам равны проекциям ускорений объемных сил;

, ,

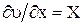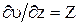
Такая функция называется силовой, или потенциальной.

Таким образом,

При этом уравнение (1) принимает вид (2)

и может быть проинтегрировано.

Рассмотрим наиболее часто встречающийся на практике случай равновесия тяжелой (т.е. находящейся под воздействием одной только силы тяжести), однородной 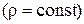капельной жидкости. При этом проекции ускорения объемных сил будут равны: Х=0, Y=0, Z=­g, и уравнение (2) получит следующую форму записи:

или, что то же самое, .

Проинтегрировав последнее уравнение, найдем: (3)

Постоянная интегрирования С может быть определенна, например, из условий на свободной поверхности жидкости. Обозначив через 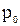давление в какой-нибудь точке этой поверхности, а через 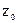ее ординату, будем иметь: или

,

где - глубина погружения рассматриваемой точки под свободной поверхностью.

Последнее уравнение является фундаментальным. Оно называется основным уравнением гидростатики и показывает, что гидростатическое давление в любой точке покоящейся тяжелой капельной жидкости полностью определяется глубиной ее погружения под свободной поверхностью жидкости, или под какой-либо другой поверхностью с известным на ней давлением, говоря иначе, изменяется в зависимости только от вертикальной координаты этой точки. В этом уравнении величина может быть названа весовым давлением, поскольку она представляет ту часть полного гидростатического давления или, как говорят абсолютного давления в рассматриваемой точке, которая обусловлена весом самой жидкости. Из рассмотрения основного уравнения гидростатики заключаем, что абсолютное давление в точке равно сумме внешнего поверхностного и весового давлений. Из этого же выражения непосредственно следует, что внешнее давление на поверхность, находящейся в равновесии жидкости передается одинаково во все точки внутри жидкости (закон Паскаля). Внутри покоящейся жидкости во всех точках, погруженных на одну и ту же глубину абсолютное давление одинаково, таким образом, при равновесии жидкости под действием силы тяжести поверхность равного давления, или поверхность уровня, представляет собой горизонтальную плоскость превышение полного гидростатического давления, над атмосферным называется избыточным или манометрическим давлением:

.

Если сосуд открыт и на его свободной поверхности устанавливается атмосферное давление, то есть , то понятия весового и избыточного давления совпадают, для закрытого же сосуда, когда давление на свободной поверхности жидкости отлично от атмосферного, весовое и избыточное давление отличаются друг от друга.

Разницу между атмосферным и гидростатическим давлением называют вакуумом: