
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Взаимное расположение прямой и плоскости
|
|
Прямая может принадлежать плоскости, быть ей параллельной или пересекать плоскость. Прямая принадлежит плоскости, если две точки, принадлежащие прямой и плоскости, имеют одинаковые отметки. Следствие, вытекающее из сказанного: точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Прямая параллельна плоскости, если она параллельна прямой, лежащей в этой плоскости.
Прямая, пересекающая плоскость. Чтобы найти точку пересечения прямой с плоскостью, необходимо (рис. 3.28):
1) через заданную прямую m провести вспомогательную плоскость Т;
2) построить линию n пересечения заданной плоскости Σ с вспомогательной плоскостью Т;
3) отметить точку пересечения R, заданной прямой m с линией пересечения n.

Рис. 3.28
Рассмотрим задачу (рис. 3.29).Прямая m задана на плане точкой А6 и углом наклона 35°. Через эту прямую проведена вспомогательная вертикальная плоскость Т, которая пересекает плоскость Σ по линии n (В2 С3 ). Таким образом, переходят от взаимного положения прямой и плоскости к взаимному положению двух прямых, лежащих в одной вертикальной плоскости. Такая задача решается построением профилей этих прямых. Пересечение прямых m и n на профиле определяет искомую точку R. Высотную отметку точки R определяют по шкале вертикальных масштабов.
Прямая, перпендикулярная плоскости. Прямая линия перпендикулярна к плоскости, если она перпендикулярна к любым двум пересекающимся прямым этой плоскости. На рис 3.30 изображена прямая m, перпендикулярная к плоскости Σ и пересекающая ее в точке А. На плане проекции прямой m и горизонтали плоскости взаимно перпендикулярны (прямой угол, одна сторона которого параллельна плоскости проекций, проецируется без искажения. Обе прямые лежат в одной вертикальной плоскости, следовательно заложения у таких прямых обратны по величине друг другу: l m = l /l u. Но l uΣ = l Σ , тогда l m = l / l Σ , то есть заложение прямой m обратно пропорционально заложению плоскости. Падения у прямой и плоскости направлены в разные стороны.

Рис. 3.29
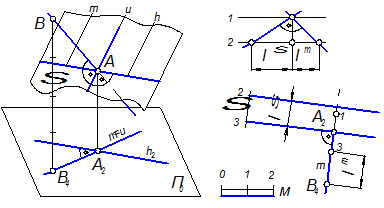
Рис. 3.30
3.4. Проекции с числовыми отметками. Поверхности
3.4.1.Многогранники и кривые поверхности. Топографическая поверхность
В природе многие вещества имеют кристаллическое строение в виде многогранников. Многогранником называют совокупность плоских многоугольников, не лежащих в одной и той же плоскости, где каждая сторона одного из них является одновременно стороной другого. При изображении многогранника достаточно указать проекции его вершин, соединив их в определенном порядке прямыми линиями - проекциями ребер. При этом на чертеже необходимо указывать видимые и невидимые ребра. На рис. 3.31 изображены призма и пирамида, а также нахождение отметок точек, принадлежащих данным поверхностям.

Рис. 3.31
Особой группой выпуклых многоугольников является группа правильных многоугольников, у которых все грани - равные между собой правильные многоугольники и все многоугольные углы равны. Существует пять видов правильных многоугольников.

Рис. 3.32
Тетраэдр - правильный четырехугольник, ограниченный равносторонними треугольниками, имеет 4 вершины и 6 ребер (рис. 3.32 а).
Гексаэдр - правильный шестигранник (куб) - 8 вершин, 12 ребер (рис. 3.32б).
Октаэдр - правильный восьмигранник, ограниченный восемью равносторонними треугольниками - 6 вершин, 12 ребер (рис. 3.32в).
Додекаэдр - правильный двенадцатигранник, ограниченный двенадцатью правильными пятиугольниками, соединенными по три около каждой вершины.
Имеет 20 вершин и 30 ребер (рис.3.32 г).
Икосаэдр - правильный двадцатигранник, ограниченный двадцатью равносторонними треугольниками, соединенными по пяти около каждой вершины.12 вершин и 30 ребер (рис. 3.32 д).
При построении точки, лежащей на грани многогранника, необходимо провести прямую, принадлежащую этой грани и на ее проекции отметить проекцию точки.
Конические поверхности образуются перемещением прямолинейной образующей по криволинейной направляющей так, что во всех положениях образующая проходит через неподвижную точку -вершину поверхности. Конические поверхности общего вида на плане изображают направляющей горизонталью и вершиной. На рис. 3.33 показано нахождение отметки точки на поверхности конической поверхности.

Рис. 3.33
Прямой круговой конус изображается серией концентрических окружностей, проведенных через равные интервалы (рис.3.34а). Эллиптический конус с круговым основанием - серией эксцентрических окружностей (рис. 3.34 б)

Рис. 3.34
Сферические поверхности. Сферическую поверхность относят к поверхностям вращения. Она образуется вращением окружности вокруг ее диаметра. На плане сферическая поверхность определена центром К и проекцией одной из ее горизонталей (экватором сферы) (рис. 3.35).

Рис. 3.35
Топографическая поверхность. Топографическую поверхность относят к геометрически неправильным поверхностям, так как она не имеет геометрического закона образования. Для характеристики поверхности определяют положение ее характерных точек относительно плоскости проекций. На рис. 3.3 б а дан пример участка топографической поверхности, на котором показаны проекции ее отдельных точек. Такой план хотя и дает возможность составить представление о форме изображаемой поверхности, однако отличается малой наглядностью. Чтобы придать чертежу большую наглядность и облегчить тем самым его чтение, проекции точек с одинаковыми отметками соединяют плавными кривыми линиями, которые называют горизонталями (изолиниями) (рис. 3.36 б).

Рис. 3.36
Горизонтали топографической поверхности иногда определяют и как линии пересечения этой поверхности с горизонтальными плоскостями, отстоящими друг от друга на одно и то же расстояние (рис. 3.37). Разность отметок у двух смежных горизонталей называют высотой сечения.
Изображение топографической поверхности тем точнее, чем меньше разность отметок у двух смежных горизонталей. На планах горизонтали замыкаются в пределах чертежа или вне его. На более крутых склонах поверхности проекции горизонталей сближаются, на пологих – их проекции расходятся.

Рис. 3.37
Кратчайшее расстояние между проекциями двух смежных горизонталей на плане называют заложением. На рис. 3.38 через точку А топографической поверхности проведено несколько отрезков прямых АВ, АС и АD. Все они имеют разные углы падения. Наибольший угол падения имеет отрезок АС, заложение которого имеет минимальное значение. Поэтому он и будет являться проекцией линии падения поверхности в данном месте.

Рис. 3.38
На рис. 3.39 приводится пример построения проекции линии падения через заданную точку А. Из точки А100 , как из центра, проводят дугу окружности, касающуюся ближайшей горизонтали в точке В90. Точка В90 , лежащая на горизонтали h90 , будет принадлежать линии падения. Из точки В90 проводят дугу, касающуюся следующей горизонтали в точке С80 , и т. д. Из чертежа видно, что линией падения топографической поверхности является ломаная линия, каждое звено которой перпендикулярно к горизонтали, проходящей через нижний, имеющий меньшую отметку, конец звена.

Рис. 3.39
3.4.2.Пересечение конической поверхности плоскостью
Если секущая плоскость проходит через вершину конической поверхности, то она пересекает ее по прямым линиям-образующим поверхности. Во всех остальных случаях линия сечения будет плоской кривой: окружностью, эллипсом и т.д. Рассмотрим случай пересечения конической поверхности плоскостью.
Пример 1. Построить проекцию линии пересечения кругового конуса Φ (hо, S5 ) с плоскостью Ω, параллельной образующей конической поверхности.
Коническая поверхность при заданном расположении плоскости пересекается по параболе. Проинтерполировав образующую t строим горизонтали кругового конуса - концентрические окружности с центром S 5. Затем определяем точки пересечения одноименных горизонталей плоскости и конуса (рис. 3.40).

Рис. 3.40
3.4.3. Пересечение топографической поверхности с плоскостью и прямой линией
Случай пересечения топографической поверхности с плоскостью наиболее часто встречается в решении геологических задач. На рис. 3.41 дан пример построения пересечения топографической поверхности с плоскостью Σ. Искомую кривую m определяют точками пересечения одноименных горизонталей плоскости и топографической поверхности.

Рис. 3.41
На рис. 3.42 дан пример построения истинного вида топографической поверхности с вертикальной плоскостью Σ. Искомую линию m определяют точками А, В, С … пересечения горизонталей топографической поверхности с секущей плоскостью Σ. На плане проекция кривой вырождается в прямую линию, совпадающую с проекцией плоскости: m ≡ Σ. Профиль кривой m построен с учетом расположения на плане проекций ее точек, а также их высотных отметок.

Рис. 3.42
3.4.4. Поверхность равного уклона
Поверхность равного уклона представляет собой линейчатую поверхность, все прямолинейные образующие которой составляют с горизонтальной плоскостью постоянный угол. Получить такую поверхность можно перемещением прямого кругового конуса с осью, перпендикулярной плоскости плана, так, что бы его вершина скользила по некоторой направляющей, а ось в любом положении оставалась вертикальной.
На рис. 3.43 изображена поверхность равного уклона (i=1/2), направляющей которой служит пространственная кривая A, B, C, D.

Рис. 3.43
Градуирования плоскости. В качестве примеров рассмотрим плоскости откосов дорожного полотна.
Пример 1. Продольный уклон дорожного полотна i=0, уклон откоса насыпи iн=1: 1, 5, (рис. 3.44а). Требуется провести горизонтали через 1м. Решение сводится к следующему. Проводим масштаб уклона плоскости перпендикулярно бровке дорожного полотна, отмечаем точки на расстоянии, равном интервалу 1, 5м, взятом с линейного масштаба, и определяем отметки 49, 48 и 47. Через полученные точки проводим горизонтали откоса параллельно бровке дороги.

Рис. 3.44
Пример 2. Продольный уклон дороги i≠ 0, уклон откоса насыпи iн=1: 1, 5, (рис.3.44б). Плоскость дорожного полотна градуируется. Откос дорожного полотна градуируется следующим образом. В точке с вершиной 50, 00 (или другой точке) помещаем вершину конуса, описываем окружность радиусом, равным интервалу откоса насыпи (в нашем примере l = 1, 5м). Отметка этой горизонтали конуса будет на единицу меньше отметки вершины, т.е. 49м. Проводим ряд окружностей, получаем отметки горизонталей 48, 47, касательно к которым из точек бровки с отметками 49, 48, 47 проводим горизонтали откоса насыпи.
Градуирование поверхностей.
Пример 3. Если продольный уклон дороги i=0 и уклон откоса насыпи iн=1: 1, 5, то горизонтали откосов проводят через точки масштаба уклона, интервал которого равен интервалу откосов насыпи, (рис.3.45а). Расстояние между двумя проекциями смежных горизонталей в направлении общей нормы (масштаб уклона) всюду одинаково.

Рис. 3.45
Пример 4. Если продольный уклон дороги i≠ 0, а уклон откоса насыпи iн=1: 1, 5, (рис.3.45б) то горизонтали строят аналогично, за исключением того, что горизонтали откоса проводят не прямыми линиями, а кривыми.
3.4.5. Определение линии пределов земляных работ
Так как большинство грунтов неспособно сохранять вертикальные стенки, приходится строить откосы (искусственные сооружения). Уклон, придаваемый откосом, зависит от грунта.
Чтобы участку поверхности земли придать вид плоскости с определённым уклоном, нужно знать линию пределов земляных и нулевых работ. Эта линия, ограничивающая планируемый участок, представляется линиями пересечения откосов насыпей и выемок с заданной топографической поверхностью.
Так как каждая поверхность (в том числе и плоская) изображается при помощи горизонталей, то линию пересечения поверхностей строят как множество точек пересечения горизонталей с одинаковыми отметками. Рассмотрим примеры.
Пример 1. На рис. 3.46 дано земляное сооружение, имеющее форму усеченной четырехугольной пирамиды, стоящее на плоскости Н. Верхнее основание АВСD пирамиды имеет отметку 4м и размеры сторон 2× 2, 5 м. Боковые грани (откосы насыпи) имеет уклон 2: 1 и 1: 1, направление которых показано стрелками.

Рис. 3.46
Нужно построить линию пересечения откосов сооружения с плоскостью Н и между собой, а также построить, продольный профиль по оси симметрии.
Вначале строят диаграмму уклонов, интервалов и масштабов заложений, заданных откосов. Перпендикулярно каждой стороне площадки вычерчиваются масштабы уклонов откосов с заданными интервалами, после чего проекции горизонталей с одинаковыми отметками смежных граней находятся линии пересечения откосов, которые являются проекциями боковых ребер данной пирамиды.
Нижнее основание пирамиды совпадает с нулевыми горизонталями откосов. Если данное земляное сооружение пересечь вертикальной плоскостью Q, в сечении получится ломаная линия – продольный профиль сооружения.
Пример 2. Построить линию пересечения откосов котлована с плоским косогором и между собой. Дно (АВСD) котлована представляет собой прямоугольную площадку с отметкой 10м и размерами 3× 4м. Ось площадки составляет с линией юг – север угол 5°. Откосы выемок имеют одинаковые уклоны 2: 1 (рис. 3.47).

Рис.3.47
Линия нулевых работ устанавливается по плану местности. Её строят по точкам пересечения между собой одноименных проекций горизонталей рассматриваемых поверхностей. По точкам пересечения горизонталей откосов и топографической поверхности с одинаковыми отметками находят линию пересечения откосов, которые являются проекциями боковых ребер данного котлована.
В данном случае к дну котлована примыкают боковые откосы выемок. Линия abcd – искомая линия пересечения. Aa, Bb, Сс, Dd – ребра котлована, линии пересечения откосов между собой.
4. Вопросы для самоконтроля и задачи для самостоятельной работы по теме «Прямоугольные проекции»
Точка
4.1.1. Сущность метода проекций.
4.1.2. Что такое проекция точки?
4.1.3. Как называются и обозначаются плоскости проекций?
4.1.4. Что такое линии проекционной связи на чертеже и как они располагаются на чертеже по отношению к осям проекций?
4.1.5. Как построить третью (профильную) проекцию точки?
4.1.6. Построить на трехкартинном чертеже три проекции точек А, В, С, записать их координаты и заполнить таблицу.
 |
А …, …, …
B …, …, …
С …, …, …
| Обозначение | Название элемента чертежа |
| П1 | |
| П2 | |
| П3 | |
| x, y, z | |
| A1 | |
| A2 | |
| A3 | |
| A1A2 | |
| A2A3 |
4.1.7. Построить недостающие оси проекций, хА=25, yA=20. Построить профильную проекцию точки А.

4.1.8. Построить три проекции точек по их координатам: А(25, 20, 15), В(20, 25, 0) и С(35, 0, 10). Указать положение точек по отношению к плоскостям и осям проекций. Какая из точек ближе к плоскости П3?

4.1.9. Материальные точки А и В начинают одновременно падать. В каком положении окажется точка В, когда точка А коснется земли? Определить видимость точек. Построить точки в новом положении.

4.1.10. Построить три проекции точки А, если точка лежит в плоскости П3, а расстояние от нее до плоскости П1 равно 20 мм, до плоскости П2 – 30 мм. Записать координаты точки.

Прямая
4.2.1. Чем может быть задана прямая линия на чертеже?
4.2.2. Какая прямая называется прямой общего положения?
4.2.3. Какое положение может занимать прямая относительно плоскостей проекций?
4.2.4. В каком случае проекция прямой обращается в точку?
4.2.5. Что характерно для комплексного чертежа прямой уровня?
4.2.6. Определить взаимное положение данных прямых.

a … b a … b a … b
4.2.7. Построить проекции отрезка прямой АВ длиной 20 мм, параллельного плоскостям: а) П2; б) П1; в) оси Ох. Обозначить углы наклона отрезка к плоскостям проекций.
a) б) в)

4.2.8. Построить проекции отрезка АВ по координатам его концов: А(30, 10, 10), В(10, 15, 30). Построить проекции точки С, делящей отрезок в отношении АС: СВ = 1: 2.

4.2.9. Определить и записать количество ребер данного многогранника и положение их относительно плоскостей проекций.

4.2.10. Через точку А провести горизонталь и фронталь, пересекающие прямую m.

4.2.11. Определить расстояние между прямой b и точкой А

4.2.12. Построить проекции отрезка АВ длиной 20 мм, проходящего через точку А и перпендикулярного плоскости а) П2; б) П1; в) П3.
а) б)

в)
