
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тангенциальная составляющая ускорения 2 страница
|
|
Закон сохранения импульса является следствием определенного свойства симметрии пространства — его однородности. Однородность пространства заключается в том, что при параллельном переносе в пространстве замкнутой системы тел как целого ее физические свойства и законы движения не изменяются, иными словами, не зависят от выбора положения начала координат инерциальной системы отсчета.
Отметим, что, согласно (9.1), импульс сохраняется и для незамкнутой системы, если геометрическая сумма всех внешних сил равна нулю.
В механике Галилея—Ньютона из-за независимости массы от скорости импульс системы может быть выражен через скорость ее центра масс. Центром масс (или центром инерции) системы материальных точек называется воображаемая точка С, положение которой характеризует распределение массы этой системы. Ее радиус-вектор равен

где mi и ri — соответственно масса и радиус-вектор i -й материальной точки; n — число материальных точек в системе; 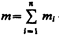 – масса системы. Скорость центра масс
– масса системы. Скорость центра масс

Учитывая, что pi = mi v i, a  есть импульс р системы, можно написать
есть импульс р системы, можно написать
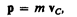 (9.2)
(9.2)
т. е. импульс системы равен произведению массы системы на скорость ее центра масс.
Подставив выражение (9.2) в уравнение (9.1), получим
 (9.3)
(9.3)
т. е. центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, приложенных к системе. Выражение (9.3) представляет собой закон движения центра масс.
В соответствии с (9.2) из закона сохранения импульса вытекает, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.
§ 10. Уравнение движения тела переменной массы
Движение некоторых тел сопровождается изменением их массы, например масса ракеты уменьшается вследствие истечения газов, образующихся при сгорании топлива, и т. п.
Выведем уравнение движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты m, а ее скорость v, то по истечении времени d t ее масса уменьшится на d m и станет равной т — d m, а скорость станет равной v + dv. Изменение импульса системы за отрезок времени d t

где u — скорость истечения газов относительно ракеты. Тогда

(учли, что d m dv — малый высшего порядка малости по сравнению с остальными). Если на систему действуют внешние силы, то dp=Fd t, поэтому
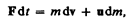
или
 (10.1)
(10.1)
Второе слагаемое в правой части (10.1) называют реактивной силой Fp. Если u противоположен v по направлению, то ракета ускоряется, а если совпадает с v, то тормозится.
Таким образом, мы получили уравнение движения тела переменной массы
 (10.2)
(10.2)
которое впервые было выведено И. В. Мещерским (1859—1935).
Идея применения реактивной силы для создания летательных аппаратов высказывалась в 1881 г. Н. И. Кибальчичем (1854—1881). К. Э. Циолковский (1857—1935) в 1903 г. опубликовал статью, где предложил теорию движения ракеты и основы теории жидкостного реактивного двигателя. Поэтому его считают основателем отечественной космонавтики.

Применим уравнение (10.1) к движению ракеты, на которую не действуют никакие внешние силы. Полагая F=0 и считая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим

откуда

Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени скорость ракеты равна нулю, а ее стартовая масса m 0, то С = u ln(m 0). Следовательно,
v = u ln (m 0/ m). (10.3)
Это соотношение называется формулой Циолковского. Она показывает, что: 1) чем больше конечная масса ракеты т, тем больше должна быть стартовая масса ракеты m 0; 2) чем больше скорость истечения и газов, тем больше может быть конечная масса при данной стартовой массе ракеты.
Выражения (10.2) и (10.3) получены для нерелятивистских движений, т. е. для случаев, когда скорости v и u малы по сравнению со скоростью с распространения света в вакууме.
Задачи
2.1. По наклонной плоскости с углом наклона а к горизонту, равным 30°, скользит тело. Определить скорость тела в конце третьей секунды от начала скольжения, если коэффициент трения 0, 15. [10, 9 м/с]
2.2. Самолет описывает петлю Нестерова радиусом 80 м. Какова должна быть наименьшая скорость самолета, чтобы летчик не оторвался от сиденья в верхней части петли? [28 м/с]
2.3. Блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы a = 30° и b=45°. Гири равной массы (m1=m2=2 кг) соединены нитью, перекинутой через блок. Считая нить и блок невесомыми, принимая коэффициенты трения гирь о наклонные плоскости равными f 1= f 2= f =0, 1 и пренебрегая трением в блоке, определить: 1) ускорение, с которым движутся гири; 2) силу натяжения нити. [1) 0, 24 м/с2; 2) 12 Н]
2.4. На железнодорожной платформе установлена безоткатная пушка, из которой производится выстрел вдоль полотна под углом a=45° к горизонту. Масса платформы с пушкой М =20 т, масса снаряда m =10 кг, коэффициент трения между колесами платформы и рельсами f = 0, 002. Определить скорость снаряда, если после выстрела платформа откатилась на расстояние s =3 м. [ v 0=M 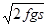 /(mcosa)=970м/с]
/(mcosa)=970м/с]
2.5. На катере массой m =5 т находится водомет,.выбрасывающий μ =25 кг/с воды со скоростью и=7 м/с относительно катера назад. Пренебрегая сопротивлением движению катера, определить: 1) скорость катера через 3 мин после начала движения; 2) предельно возможную скорость катера. [1) v=u (1—exp(– μ t / m) = 4, 15 м/с; 2) 7 м/с]
Глава 3 Работа и энергия
§11. Энергия, работа, мощность
Энергия — универсальная мера различных форм движения и взаимодействия. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др. В одних явлениях форма движения материи не изменяется (например, горячее тело нагревает холодное), в других — переходит в иную форму (например, в результате трения механическое движение превращается в тепловое). Однако существенно, что во всех случаях энергия, отданная (в той иди иной форме) одним телом другому телу, равна энергии, полученной последним телом.
Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол a с направлением перемещения, то работа этой силы равна произведению проекции силы Fs на направление перемещения (Fs = F cosa), умноженной на перемещение точки приложения силы:
 (11.1)
(11.1)
В общем случае сила может изменяться как по модулю, так и по направлению, поэтому формулой (11.1) пользоваться нельзя. Если, однако, рассмотреть элементарное перемещение dr, то силу F можно считать постоянной, а движение точки ее приложения — прямолинейным. Элементарной работой силы F на перемещении dr называется скалярная величина

где a — угол между векторами F и dr; ds = |dr| — элементарный путь; Fs — проекция вектора F на вектор dr (рис. 13).
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сумма приводится к интегралу
 (11.2)
(11.2)

Для вычисления этого интеграла надо знать зависимость силы Fs, от пути s вдоль траектории 1 — 2. Пусть эта зависимость представлена графически (рис. 14), тогда искомая работа А определяется на графике площадью заштрихованной фигуры. Если, например, тело движется прямолинейно, сила F=const и a=const, то получим

где s — пройденный телом путь (см. также формулу (11.1)).
Из формулы (11.1) следует, что при a < p/2 работа силы положительна, в этом случае составляющая F s совпадает по направлению с вектором скорости движения v (см. рис. 13). Если a > p/2, то работа силы отрицательна. При a = p/2 (сила направлена перпендикулярно перемещению) работа силы равна нулю.
Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж=1 Н × м).
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности:
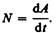 (11.3)
(11.3)
За время d t силаF совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени

т. е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная.
Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
§ 12. Кинетическая и потенциальная энергии
Кинетическая энергия механической системы — это энергия механического движения этой системы.
Сила F, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа d A силы F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии d T тела, т. е.

Используя второй закон Ньютона  и умножая на перемещение dr получаем
и умножая на перемещение dr получаем


Так как  то d A = mv d v =mvdv= d T, откуда
то d A = mv d v =mvdv= d T, откуда

Таким образом, тело массой т, движущееся со скоростью v, обладает кинетической энергией
 (12.1)
(12.1)
Из формулы (12.1) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения.
При выводе формулы (12.1) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньютона. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.
Потенциальная энергия — механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, — консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипатнвной; ее примером является сила трения.
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
 (12.2)
(12.2)
Работа d A выражается как скалярное произведение силы F на перемещение dr и выражение (12.2) можно записать в виде
 (12.3)
(12.3)
Следовательно, если известна функция П(r), то из формулы (12.3) можно найти силу F по модулю и направлению.
Потенциальная энергия может быть определена исходя из (12.3) как

где С — постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня. Для консервативных сил
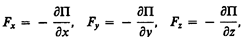
или в векторном виде
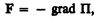 (12.4)
(12.4)
где
 (12.5)
(12.5)
(i, j, k — единичные векторы координатных осей). Вектор, определяемый выражением (12.5), называется градиентом скаляра П.
Для него наряду с обозначением grad П применяется также обозначение Ñ П. Ñ («набла») означает символический вектор, называемый оператором Гамильтона* или набла-оператором:
 (12.6)
(12.6)
* У. Гамильтон (1805—1865) — ирландский математик и физик.
Конкретный вид функции П зависит от характера силового поля. Например, потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, равна
 (12.7)
(12.7)
где высота h отсчитывается от нулевого уровня, для которого П0=0. Выражение (12.7) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h'), П= —mgh'.
Найдем потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:

где Fx упp — проекция силы упругости на ось х; k — коэффициент упругости (для пружины — жесткость), а знак минус указывает, что Fx упpнаправлена в сторону, противоположную деформации x.
По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.
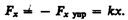
Элементарная работа d A, совершаемая силой Fx при бесконечно малой деформации d x, равна

а полная работа

идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела
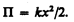
Потенциальная энергия системы является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы — энергия механического движения и взаимодействия:

т. е. равна сумме кинетической и потенциальной энергий.
§ 13. Закон сохранения энергии
Закон сохранения энергии — результат обобщения многих экспериментальных данных. Идея этого закона принадлежит М. В. Ломоносову (1711—1765), изложившему закон сохранения материи и движения, а количественная формулировка закона сохранения энергии дана немецким врачом Ю. Майером (1814—1878) и немецким естествоиспытателем Г. Гельмгольцем (1821—1894).
Рассмотрим систему материальных точек массами m 1, m 2,..., mn, движущихся со скоростями v1, v2,..., v n. Пусть  ,
,  ,...,
,...,  — равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, a F1, F2,..., F n — равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначимf1, f2,..., f n. При v< < c массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:
— равнодействующие внутренних консервативных сил, действующих на каждую из этих точек, a F1, F2,..., F n — равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действуют еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначимf1, f2,..., f n. При v< < c массы материальных точек постоянны и уравнения второго закона Ньютона для этих точек следующие:

Двигаясь под действием сил, точки системы за интервал времени d t совершают перемещения, соответственно равные dr1, dr2,..., dr n. Умножим каждое из уравнений скалярно на соответствующее перемещение и, учитывая, что dr i ==v i d t, получим


Сложив эти уравнения, получим
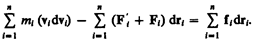 (13.1)
(13.1)
Первый член левой части равенства (13.1)

где d T — приращение кинетической энергии системы. Второй член  равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dП системы (см. (12.2)).
равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dП системы (см. (12.2)).
Правая часть равенства (13.1) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем
 (13.2)
(13.2)
При переходе системы из состояния 1 в какое-либо состояние 2

т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (13.2) следует, что
d (T +П) = 0,
откуда
 (13.3)
(13.3)
т. е. полная механическая энергия системы сохраняется постоянной. Выражение (13.3) представляет собой закон сохранение механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.
Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Закон сохранения механической энергии можно сформулировать так: в консервативных системах полная механическая энергия сохраняется.
Закон сохранения механической энергии связан с однородностью времени. Однородность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчета времени. Например, при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.
Существует еще один вид систем — диссипативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии. Строго говоря, все системы в природе являются диссипативными.
В консервативных системах полная механическая энергия остается постоянной. Могут происходить лишь превращения кинетической энергии в потенциальную и обратно в эквивалентных количествах так, что полная энергия остается неизменной. Этот закон не есть просто закон количественного сохранения энергии, а закон сохранения и превращения энергии, выражающий и качественную сторону взаимного превращения различных форм движения друг в друга. Закон сохранения и превращения энергии — фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.
В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.
§ 14. Графическом представление энергии
Во многих задачах рассматривается одномерное движение тела, потенциальная энергия которого является функцией лишь одной переменной (например, координаты х), т. е. П=П (х). График зависимости потенциальной энергии от некоторого аргумента называется потенциальной кривой. Анализ потенциальных кривых позволяет определить характер движения тела.
Будем рассматривать только консервативные системы, т. е. системы, в которых взаимные превращения механической энергии в другие виды отсутствуют. Тогда справедлив закон сохранения энергии в форме (13.3). Рассмотрим графическое представление потенциальной энергии для тела в однородном поле тяжести и для упругодеформированного тела.
Потенциальная энергия тела массой т, поднятого на высоту h над поверхностью Земли, согласно (12.7), П (h)=mgh. График данной зависимости П = П(h) — прямая линия, проходящая через начало координат (рис. 15), угол наклона которой к оси h тем больше, чем больше масса тела (так как tga =mg).
Пусть полная энергия тела равна Е (ее график — прямая, параллельная оси h). На высоте h тело обладает потенциальной энергией П, которая определяется отрезком вертикали, заключенным между точкой h на оси абсцисс и графиком П(h). Естественно, что кинетическая энергия Т задается ординатой между графиком П(h) и горизонтальной прямой ЕЕ. Из рис. 15 следует, что если h=hmax, то Т =0 и П =E=mghmax, т. е.потенциальная энергия становится максимальной и равной полной энергии.
Из приведенного графика можно найти скорость тела на высоте h:

откуда

Зависимость потенциальной энергии упругой деформации П =кх 2 / 2от деформации х имеет вид параболы (рис. 16), где график заданной полной энергии тела Е — прямая, параллельная оси абсцисс х, а значения Т и П определяются так же, как на рис. 15. Из рис. 16 следует, что с возрастанием деформации х потенциальная энергия тела возрастает, а кинетическая — уменьшается. Абсцисса x max определяет максимально возможную деформацию растяжения тела, a – х max — максимально возможную деформацию сжатия тела. Если х = ± х max, то T= 0 и П =E=k  / 2, т. е. потенциальная энергия становится максимальной и равной полной энергии.
/ 2, т. е. потенциальная энергия становится максимальной и равной полной энергии.

Из анализа графика на рис. 16 вытекает, что при полной энергии тела, равной Е, тело не может сместиться правее х max и левее – х max, так как кинетическая энергия не может быть отрицательной и, следовательно, потенциальная энергия не может быть больше полной энергии. В таком случае говорят, что тело находится в потенциальной яме с координатами – х max £ x £ х max.
В общем случае потенциальная кривая может иметь довольно сложный вид, например с несколькими чередующимися максимумами и минимумами (рис. 17). Проанализируем эту потенциальную кривую. Если Е — заданная полная энергия частицы, то частица может находиться только там, где П(х) £ Е, т. е. в областях I и III. Переходить из области I в III и обратно частица не может, так как ей препятствует потенциальный барьер CDG, ширина которого равна интервалу значений х, при которых E < П, а его высота определяется разностью Пmах– E. Для того чтобы частица смогла преодолеть потенциальный барьер, ей необходимо сообщить дополнительную энергию, равную высоте барьера или превышающую ее. В области I частица с полной энергией Е оказывается «запертой» в потенциальной яме AВС и совершает колебания между точками с координатами хA и хC.