
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгоритм вычисления конечных сумм и произведений.
|
|
Для расчета суммы 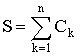 (где Ck - некоторое слагаемое, зависящее от индекса суммирования k) рационально использовать цикл по переменной – индексу суммирования. Блок схема алгоритма представлена на рис. 28.1 а.
(где Ck - некоторое слагаемое, зависящее от индекса суммирования k) рационально использовать цикл по переменной – индексу суммирования. Блок схема алгоритма представлена на рис. 28.1 а.
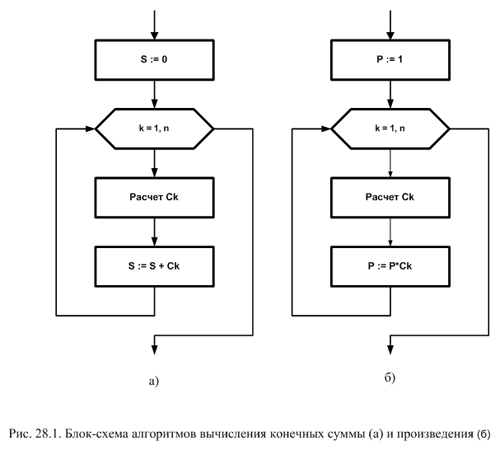
На том же рисунке представлена блок-схема расчета произведения  , где Ck - сомножитель, зависящий от индекса суммирования k.
, где Ck - сомножитель, зависящий от индекса суммирования k.
Эти алгоритмы очень похожи. Только при вычислении суммы переменной S, накапливающей ее, первоначально присваивается нулевое значение, а переменной P, накапливающей произведение – единичное. В теле цикла производится расчет слагаемого (сомножителя), а за-тем суммированием (умножением) накапливается сумма (произведение).
Вычисление бесконечных сумм возможно только для сходящихся рядов, например,  . С ростом k каждое слагаемое должно уменьшаться и сумма стремиться к определенному значению. Цикл суммирования можно прекратить, когда очередное слагаемое по абсолютной величине станет меньше заданной величины. Так как в этом случае обычно нельзя заранее вычислить число повторений, следует использовать цикл с предусловием или цикл с послеусловием. Их блок-схемы приведены на рис. 28.2.
. С ростом k каждое слагаемое должно уменьшаться и сумма стремиться к определенному значению. Цикл суммирования можно прекратить, когда очередное слагаемое по абсолютной величине станет меньше заданной величины. Так как в этом случае обычно нельзя заранее вычислить число повторений, следует использовать цикл с предусловием или цикл с послеусловием. Их блок-схемы приведены на рис. 28.2.
Перед началом циклов выполняются начальные установки: счетчик циклов k – индекс суммирования и переменная S, накапливающая сумму, обнуляются. В теле цикла сначала индекс суммирования увеличивается на единицу, а затем вычисляется слагаемое и накапливается сумма. Условием повторения цикла является | Ck| ≥ ε. Перед началом цикла с предусловием переменной Ck - слагаемому, значение которого вычисляется в теле цикла, необходимо присвоить такое начальное значение, чтобы условие повторения цикла выполнялось. В цикле с послеусловием этого не требуется.
Аналогично можно представить алгоритмы расчета бесконечных произведений, сходящихся к определенному значению.