
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введение. Постановка задачи и доказательство единственности решения .. ..6
|
|
Постановка задачи и доказательство единственности решения …..…..6
§2. Доказательство существования решения задачи 1 ………..……………19
§3. Случай, когда  и
и 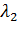 – комплексные параметры ………………………30
– комплексные параметры ………………………30
Литература ……………………………………………………………………..33
Введение
Теория уравнений смешанного типа – один из основных разделов современной теории дифференциальных уравнений с частными производными, возникшая за последние 80 лет и развивающаяся особенно интенсивно, начиная с 50-х годов. Эта теория получила интенсивное развитие в последнее время, так как появилось достаточно много прикладных задач, математическое моделирование которых обусловливает изучение различных типов уравнений в рассматриваемой области изменения независимых переменных. Первые фундаментальные результаты в этом направлении были получены Ф.Трикоми.
Существует ряд работ отечественных и зарубежных математиков, в которых исследуются основные смешанные краевые задачи и ставятся новые корректные задачи для уравнений смешанного типа.
Отечественные математики внесли существенный вклад в развитие теории уравнений смешанного типа Ф.И.Франкль обнаружил важные приложения задачи Трикоми и других родственных ей задач в трансзвуковой газодинамике. Академик И.Н.Векуа указал на важность проблемы уравнений смешанного типа при решении задач, возникших в теории бесконечно малых изгибаний поверхностей, а также в безмоментной теории оболочек с кривизной переменного знака. А.В.Бицадзе впервые сформулировал принцип экстремума для задачи Трикоми. Позднее он был доказан и для других краевых задач для уравнений смешанного типа.
Из принципа экстремума непосредственно следует единственность решения задач.
Работы Трикоми, а также дальнейшее исследование уравнений смешанного типа вызвали интерес к изучению эллиптических и гиперболических уравнений, вырождающихся на границе области.
В настоящее время понятие уравнений смешанного типа значительно расширилось и включает всевозможные комбинации двух или трех классических типов уравнений. Интенсивное исследование уравнений смешанного типа обусловлено тем, что с одной стороны новые типы смешанных уравнений еще мало исследованы в теоретическом плане, с другой – они находят широкое применение в важных вопросах механики, физики и техники.
Курсовая работа посвящена исследованию одной краевой задачи для уравнений смешанного типа третьего порядка

в области 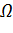 , ограниченной при
, ограниченной при  отрезками
отрезками 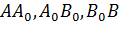 прямых
прямых  Соответственно и характеристиками
Соответственно и характеристиками 
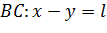 уравнения (1) при
уравнения (1) при  , где
, где  и – числовые параметры.
и – числовые параметры.
Данная работа состоит из введения и двух параграфов.
В первом параграфе дается постановка задачи, и доказывается ее однозначная разрешимость.
Задача. Найти функцию  из класса
из класса

удовлетворяющую граничным условиям



где  – заданные непрерывные функции,
– заданные непрерывные функции,  непрерывна вместе со своей производной, причем
непрерывна вместе со своей производной, причем


Пусть  .
.
Результатом данной работы является исследование однозначной разрешимости задачи для различных значений  .
.
Единственность решения задачи устанавливается методом интегралов энергии.
В первом параграфе доказаны две теоремы.
Теорема 1. Пусть  – регулярное в области решение однородной задачи, удовлетворяющее условию
– регулярное в области решение однородной задачи, удовлетворяющее условию

Тогда  в 𝛺 при всех
в 𝛺 при всех 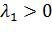 и
и 
Теорема 2. Пусть  – решение однородной задачи из класса регулярных решений уравнения (1) удовлетворяющее условию
– решение однородной задачи из класса регулярных решений уравнения (1) удовлетворяющее условию

Тогда  в 𝛺, если
в 𝛺, если  , или если
, или если  и
и  , или
, или  .
.
Во втором параграфе доказывается существование решения задачи.
Искомое решение  задачи в гиперболической части
задачи в гиперболической части 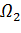 смешанной области находится как решение задачи Коши, а в области
смешанной области находится как решение задачи Коши, а в области 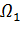 – как решение уравнения (1) при
– как решение уравнения (1) при  , удовлетворяющее граничным условиям (2) и условию
, удовлетворяющее граничным условиям (2) и условию

Эта задача эквивалентно редуцируется к интегральному уравнению Фредгольма второго рода

где  – известная функция,
– известная функция,  - функция Грина краевой задачи (2) и
- функция Грина краевой задачи (2) и  для уравнения
для уравнения  , которое в силу единственности решения задачи однозначно разрешимо.
, которое в силу единственности решения задачи однозначно разрешимо.