
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Физическая химия
|
|
ТЕМА 1
Свойства растворов электролитов. Теория электролитической диссоциации Аррениуса. Закон разведения Оствальда. Понятие об электролитической теории Дебая-Гюккеля. Активность и коэффициент активности электролитов. Средняя ионная активность и средний ионный коэффициент активности. Правило ионной силы.
Электрохимия – раздел физической химии, изучающий связь между химическими процессами и электрическими явлениями, свойства растворов электролитов, электропроводность растворов, процессы электролиза, работу гальванических элементов, электродные процессы.
1.1. СВОЙСТВА РАСТВОРОВ ЭЛЕКТРОЛИТОВ. ЗАКОН РАЗВЕДЕНИЯ ОСТВАЛЬДА. ТЕОРИЯ ЭЛЕКТРОЛИТИЧЕСКОЙ ДИССОЦИАЦИИ АРРЕНИУСА.
Вещества, подвергающиеся при взаимодействии с растворителем диссоциации на ионы и сообщающие раствору способность проводить электрический ток, называются электролитами. Ионы – электрически заряженные частицы, которые являются переносчиками электричества в растворах и расплавах.
Следует помнить, что не все электролиты диссоциируют (т.е. распадаются на ионы) в одинаковой степени. В связи с этим выделяют:
– сильные электролиты (вещества, полностью диссоциирующие в растворе);
– слабые электролиты (вещества, диссоциирующие в растворе лишь частично).
Электропроводность слабых электролитов определяется в основном степенью диссоциации a, величина которой зависит от концентрации электролита и температуры. Для любого электролита:
 . (1.1)
. (1.1)
По величине степени диссоциации судить о силе электролита не очень удобно, так как величина  зависит от многих параметров, особенно от концентрации. Более удобно использовать величину константы диссоциации К д.
зависит от многих параметров, особенно от концентрации. Более удобно использовать величину константы диссоциации К д.
Рассмотрим равновесие диссоциации слабого электролита (для простоты – бинарного, т. е. дающего при диссоциации один катион и один анион):
 ,
,
например
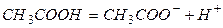 .
.
Если один моль вещества АВ растворён в V литрах раствора, то
 и
и  .
.
Константа диссоциации равна:
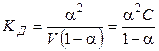 , (1.2)
, (1.2)
где С = 1/ V — начальная (исходная) концентрация вещества АВ. Выражение (1.2) называют законом разведения Оствальда для бинарных электролитов.
Очевидно, что тем больше К д, тем при данной концентрации выше степень диссоциации. Таким образом, величина К д может служить удобной мерой силы электролита. Как любая константа равновесия, константа диссоциации зависит от температуры, поэтому сила электролита меняется с изменением температуры. Выражение (1.2) позволяет определять константу диссоциации по величине степени диссоциации a при данной концентрации электролита С. С другой стороны, зная константу диссоциации, можно рассчитать величину a при любой заданной концентрации.
Проанализируем уравнение Оствальда:
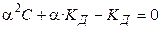 , (1.3)
, (1.3)
 , (1.4)
, (1.4)
1). 
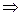
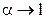 ;
;
2).  , т. е. степень диссоциации возрастает обратно пропоционально корню квадратному из концентрации электролита.
, т. е. степень диссоциации возрастает обратно пропоционально корню квадратному из концентрации электролита.
Для описания коллигативных свойств растворов электролитов используют изотонический коэффициент:
 . (1.5)
. (1.5)
Изотонический коэффициент показывает, во сколько раз суммарная эффективная концентрация недиссоциированных молекул и ионов в растворе больше по сравнению с начальной концентрацией недиссоциированных молекул. С ростом концентрации коэффициент  уменьшается.
уменьшается.
Рассмотрим как связаны  и
и  :
:
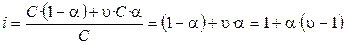 , (1.6)
, (1.6)
где υ – число ионов, на которые распадается частица (молекула). Если α = 0 (неэлектролит), то i = 1; если α = 1 (сильный электролит), то i = 2 (например,  , i = υ = 2).
, i = υ = 2).
Экспериментально величину i можно найти путем сравнения опытных значений осмотических давлений растворов, понижения температуры замерзания или повышения температуры кипения растворов со значениями, вычисленными в предположении, что i = 1 (расчетные величины):
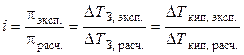 . (1.7)
. (1.7)
Следует помнить, что i ≥ 1 для растворов электролитов (они диссоциируют), если же молекулы ассоциируют (например, из двух молекул образуется одна частица за счёт водородных связей), то i < 1.
В 1883 году С. Аррениус сформулировал основные положения теории о физической природе электролитов, которые получили название теории электролитической диссоциации Аррениуса.
1. Молекулы растворенного вещества подвергаются в растворах диссоциации на катионы и анионы.
2. Диссоциация может быть полной или частичной.
3. Молекулы и образовавшиеся при диссоциации ионы находятся в равновесии.
4. По способности к диссоциации электролиты были разделены на слабые, средние и сильные.
Теория Аррениуса верна только для слабых электролитов с концентрацией С ≤ 0, 01 моль/л. Для растворов сильных электролитов она не выполняется, так как не учитывает ни ион-дипольного, ни ион-ионного взаимодействия в растворах. Например, теория Аррениуса не может объяснить, почему константы диссоциации слабых электролитов не остаются постоянными по мере разведения растворов, а у сильных электролитов степень диссоциации, определенная разными методами, оказывается различной по величине, а в концентрированных растворах иногда даже превышает единицу.
1.2. ПОНЯТИЕ ОБ ЭЛЕКТРОЛИТИЧЕСКОЙ ТЕОРИИ СИЛЬНЫХ
ЭЛЕКТРОЛИТОВ ДЕБАЯ-ГЮККЕЛЯ.
Одной из теорий, количественно учитывающих ион-ионные взаимодействия, явилась теория Дебая-Гюккеля, достаточно хорошо объясняющая свойства разбавленных растворов сильных электролитов. Степень диссоциации для сильных электролитов равна единице. Поэтому зависимость электропроводности, осмотического давления и других свойств расворов от концентрации определяется главным образом действием межионных сил и сольватационными эффектами. Под сольватацией понимают совокупность энергетических и структурных изменений, происходящих в растворе при взаимодействии частиц растворенного вещества с молекулами растворителя.
В основе теории Дебая-Гюккеля лежат следующие положения: электростатическое взаимодействие противоположно заряженных ионов приводит к тому, что вокруг положительных ионов вероятность нахождения отрицательных ионов будет больше, чем положительных. Таким образом, вокруг каждого иона как бы существует ионная атмосфера из противоположно заряженных ионов. (Сфера, в которой преобладает заряд, противоположный по знаку центральному иону, и называется ионной атмосферой). Ионная атмосфера вокруг иона содержит и положительные, и отрицательные ионы, однако в среднем вокруг каждого положительного иона имеется избыток отрицательных ионов, а вокруг отрицательного иона – избыток положительных ионов. Раствор в целом остается электронейтральным.
Химический потенциал i -го компонента в идеальном растворе равен:
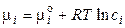 , (1.8)
, (1.8)
где сi – концентрация i -го иона в растворе. Для реального раствора:
 , (1.9)
, (1.9)
где ai = ci · fi — активность i-го иона в растворе, fi – коэффициент активности. Тогда энергия взаимодействия центрального иона с ионной атмосферой в расчете на 1 моль ионов равна
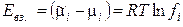 . (1.10)
. (1.10)
Таким образом, величина коэффициента активности, зависящая от силы электростатического взаимодействия ионов, степени их сольватации и ряда других эффектов, характеризует степень отклонения свойств реальных растворов электролитов от законов идеальных растворов.
1.3. АКТИВНОСТЬ И КОЭФФИЦИЕНТ АКТИВНОСТИ ЭЛЕКТРОЛИТОВ.
СРЕДНЯЯ ИОННАЯ АКТИВНОСТЬ И СРЕДНИЙ ИОННЫЙ КОЭФФИЦИЕНТ
АКТИВНОСТИ. ИОННАЯ СИЛА. ПРАВИЛО ИОННОЙ СИЛЫ.
Различают активность электролита и активность ионов. Для любого электролита процесс диссоциации можно записать следующим образом:
 ,
,
где n + и n– — количество ионов А с зарядом z + и ионов B c зарядом z –, на которые распадается исходная частица. Например, при диссоциации хлорида бария:

 .
.
Связь активности электролита с активностями ионов выражается следующим соотношением:
 , (1.11)
, (1.11)
где а — активность электролита, а + и а – — активности положительных и отрицательных ионов. Например, для бинарных электролитов справедливо:

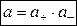 .
.
Экспериментальных методов определения активности отдельных ионов (а + и а –) не существует. Поэтому было введено понятие средней ионной активности (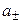 ), представляющей собой среднее геометрическое из активности отдельных ионов:
), представляющей собой среднее геометрическое из активности отдельных ионов:
 , (1.12)
, (1.12)
где 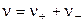 .
.
Тогда
 . (1.13)
. (1.13)
Криоскопический метод и метод, основанный на определении давления пара, позволяют определить активность электролита в целом (а) и по уравнению (7.13) найти среднюю ионную активность.
Средний ионный коэффициент активности (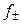 ) определяется выражением
) определяется выражением
 . (1.14)
. (1.14)
Значения 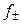 в основном определяют криоскопическим методом и методом Э.Д.С.
в основном определяют криоскопическим методом и методом Э.Д.С.
Средняя ионная моляльность (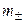 ) определяется как
) определяется как
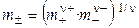 . (1.15)
. (1.15)
Если концентрацию раствора выражать через моляльность, то
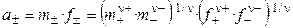 .
.
Пример 1.1. Найти связь между активностью электролита, его моляльной концентрацией и средним ионным коэффициентом активности для р-ров NaCl и Na2CO3 моляльности m.
а) Концентрации ионов, образующихся при полной диссоциации NaCl, равны m:
 .
.
Так как n + = n– = 1, то
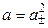 .
.
Для равновалентных электролитов средняя моляльность будет равна общей моляльности электролита:
 .
.
Тогда
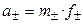 ,
,
 .
.
б) Концентрации ионов, образующихся при полной диссоциации Na2CO3, равны
 .
.
Так как n + = 2, n– = 1, то
 .
.
 ,
,
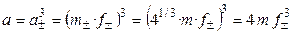 .
.
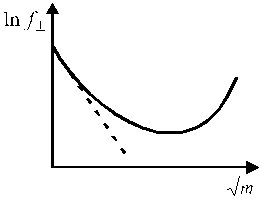 |  | ||
Средний ионный коэффициент активности зависит от концентрации раствора (рис. 1). В области предельно разбавленных растворов электролитов эта зависимость имеет линейный характер в координатах
 .
.
Рис. 1. Зависимость среднего ионного Рис. 2. Зависимость среднего коэффициента
коэффициента активности активности ионов от ионной силы раствора.
от концентрации электролита. Кривая 1 описывает экспериментальную
зависимость, кривая 2 описывает зависимость
по предельному закону Дебая-Гюккеля.
Присутствие в растворе других солей изменяет коэффициент активности данной соли и тем сильнее, чем больше заряд добавляемых ионов. Суммарную концентрацию всех ионов в растворе выражают через ионную силу раствора  , определяемую как полусумму произведений моляльностей всех ионов на квадрат их зарядов:
, определяемую как полусумму произведений моляльностей всех ионов на квадрат их зарядов:
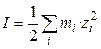 , (1.16)
, (1.16)
где mi – концентрация i -ого иона; zi – заряд i -ого иона.
Зависимость среднего коэффициента активности ионов от ионной силы раствора имеет сложный характер и представлена на рис. 2.
Пример 1.2. Определить ионную силу раствора, содержащего на 1000 г воды 0, 01 моль  и 0, 1 моль
и 0, 1 моль  .
.
Решение. Ионная сила такого раствора равна


Пример 1.3. Определить ионную силу раствора 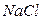 с моляльностью m = 0, 5.
с моляльностью m = 0, 5.
Решение. По уравнению (7.16) получаем
 .
.
Для растворов сильных электролитов выполняется правило ионной силы: в растворах с одинаковой ионной силой средние коэффициенты активности ионов равны. Теория сильных электролитов приводит к следующему соотношению, связывающему средние коэффициенты активности ионов с ионной силой раствора в области сильно разбавленных электролитов:
 , (1.17)
, (1.17)
где A = f (D, T) – константа, зависящая от диэлектрической проницаемости растворителя (D) и температуры (T).
Уравнение (1.17) применимо лишь при очень больших разведениях (I ≤ 0, 01, рис. 2), почему и получило название предельного закона Дебая-Гюккеля. В слабо минерализованных водах для расчета 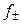 при 25 oС используется следующее уравнение:
при 25 oС используется следующее уравнение:
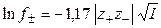 . (1.18)
. (1.18)
Для водных растворов бинарных электролитов при 25 oС справедливо:
 . (1.19)
. (1.19)
Известно, что в сильно разбавленных растворах электролитов коэффициенты активности ионов учитывают в основном поправки к их концентрациям (моляльностям), обусловленные электростатическим (ион–ионным) взаимодействием. В то же время по закону Кулона эти взаимодействия зависят также от величины зарядов и радиусов ионов. Поэтому естественно принять, как это было сделано впервые Д. Мак-Иннесом, что коэффициенты активности ионов с одинаковыми зарядами и радиусами в растворах с одинаковой ионной силой будут одинаковыми. Это предположение было названо правилом Мак–Иннеса.
Мак–Иннес предложил взять в качестве стандартов ионы калия и хлора как имеющие одинаковые заряды и радиусы гидротированных ионов. Определив значения  и
и 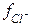 , можно затем на основе закона ионной силы вычислить коэффициенты активности всех других ионов.
, можно затем на основе закона ионной силы вычислить коэффициенты активности всех других ионов.
ТЕМА 2
Удельная и эквивалентная электропроводность, их зависимость от концентрации для сильных и слабых электролитов. Подвижность ионов. Закон независимости движения ионов Кольрауша, предельная ионная электропроводность. Аномальная подвижность ионов гидроксила и гидроксония. Экспериментальные приложения метода электропроводности.
2.1. УДЕЛЬНАЯ ЭЛЕКТРОПРОВОДНОСТЬ РАСТВОРОВ ЭЛЕКТРОЛИТОВ.
При наложении электрического поля на раствор электролита сольватированные ионы, находящиеся до этого в беспорядочном тепловом движении, начинают упорядоченное движение (миграцию) к противоположно заряженным электродам. С возрастанием скорости движения ионов возрастает сопротивление среды и через некоторое время скорость движения ионов становится постоянной.
Скорость движения ионов i -го вида определяется градиентом потенциала (напряженности) электрического поля E (В/см) и сопротивлением среды, зависящим от температуры, природы иона и растворителя:
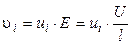 , (2.1)
, (2.1)
где U (В) – разность потенциалов между электродами, l (см) – расстояние между ними, ui (см2·В-1·с-1) – абсолютная скорость движения ионов в данных условиях (т. е. скорость движения ионов при Е = 1 В/см).
Мерой способности вещества проводить электрический ток при наложении внешенего электрического поля является электрическая проводимость (электропроводность) L. На практике эта способность часто характеризуется обратной величиной — сопротивлением проводника. Так, общее сопротивление проводника R (Ом) длиной l (см) и поперечным сечением S (см2) равно
 , (2.2)
, (2.2)
где ρ – коэффициент пропорциональности, называемый удельным сопротивлением. Из (8.2) следует, что удельное сопротивление — это сопротивление проводника длиной 1 см и сечением 1 см2, размерность его равна:
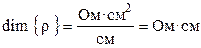 . (2.2)
. (2.2)
Удельная электропроводность электролита æ — величина, обратная удельному сопротивлению:
æ 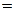
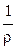
 [Ом-1·см-1]. (2.3)
[Ом-1·см-1]. (2.3)
Она характиризует электропроводность слоя электролита толщиной в 1 см с площадью поперечного сечения в 1 см2. Тогда
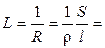 æ
æ 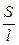 . (2.4)
. (2.4)
Удельная электропроводность раствора электролита определяется количеством ионов, переносящих электричество, и скоростью их миграции.
Пусть между электродами, находящимися на расстоянии l (см) и к которым приложена разность потенциалов U (В), находится раствор электролита (рис. 3). Для ионов i -го вида: концентрация Ci (моль-экв/см3) и скорость миграции υ i (см/с).
Рис. 3. Схема переноса зарядов через раствор электролита.
 |
Через поперечное сечение S раствора (рис. 3) за 1 с мигрирует (Ci υ i S) моль-эквивалентов ионов i -го вида, которые перенесут (
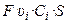 )
) 
количество электричества, где F – число Фарадея (96485 Кл/моль-экв). Количество электричества (Кл), перенесенное всеми ионами за 1 с (т. е. сила тока I в А) равно:
 (2.5)
(2.5)
Или, с учетом (8.1),
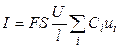 . (2.6)
. (2.6)
По закону Ома
 (æ S), (2.7)
(æ S), (2.7)
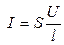 æ. (2.8)
æ. (2.8)
Тогда, из уравнений (8.6) и (8.8), для удельной электропроводности получаем
æ  . (2.9),
. (2.9),
т. е. удельная электропроводность электролита пропорциональна концентрациям ионов и их абсолютным скоростям движения. Для раствора бинарного электролита концентрации С (моль-экв/см3) со степенью диссоциации α имеем
æ  , (2.10)
, (2.10)
где u + и u ‑ ‑ абсолютные скорости движения катионов и анионов.
При повышении температуры электролита возрастают скорости движения ионов и удельная электропроводность:
æ 2 = æ 1  , (2.11)
, (2.11)
где B – температурный коэффициент (для сильных кислот 0, 016; для сильных оснований 0, 019; для солей 0, 022).
2.2. ЭКВИВАЛЕНТНАЯ ЭЛЕКТРОПРОВОДНОСТЬ.
Удельная электропроводность растворов зависит от природы электролита, природы растворителя, температуры, концентрации ионов в растворе и т. д. Хотя для понимания свойств электролитов удельная электропроводность представляет собой малоудобную величину, зато ее можно измерить непосредственно и затем пересчитать в эквивалентную электропроводность λ. Эквивалентная электропроводность представляет собой электропроводность такого объёма раствора V (см3), который содержит 1 моль-экв растворенного вещества и заключён между двумя параллельными электродами соответствующей площади, находящихся на расстоянии в 1 см друг от друга:
 æ V = æ / C, (2.12)
æ V = æ / C, (2.12)
где С – концентрация раствора (моль-экв/см3).
Эквивалентную электропроводность (Ом-1·см2·(моль-экв)-1) легко рассчитать, если известны удельная электропроводность и концентрация раствора.
Для описания температурной зависимости эквивалентной электропроводности используется следующее уравнение:
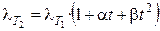 , (2.13)
, (2.13)
где a и b — эмпирические коэффициенты. Увеличение электропроводности с ростом температуры связано в основном с уменьшением вязкости раствора электролита. Обычно при повышении температуры на 1 К электропроводность увеличивается на 1, 5 – 2%.
Эквивалентная электропроводность растворов электролитов с разбавлением возрастает и в области предельных разбавлений достигает предельного значения λ ∞ , называемой электропроводностью при бесконечном разбавлении или предельной электропроводностью. Эта величина соответствует электропроводности гипотетически бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами.
Из уравнений (2.10) и (2.11) следует, что
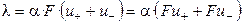 . (2.14)
. (2.14)
Произведение числа Фарадея на абсолютную скорость движения иона называют подвижностью иона:
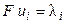 . (2.15)
. (2.15)
 , (2.16)
, (2.16)
где λ + и λ ‑ ‑ подвижности катиона и аниона соответственно. Подвижности ионов измеряются в тех же единицах, что и эквивалентная электропроводность (см2·Oм-1·моль-экв-1), поэтому их иногда называют ионными электропроводностями или электрическими проводимостями ионов.
При бесконечном разведении (α = 1) получаем
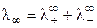 , (8.17)
, (8.17)
где  и
и 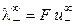 ‑ предельные подвижности ионов.
‑ предельные подвижности ионов.
Величина предельной электропроводности бесконечно разбавленного раствора электролита представляет собой сумму двух независимых слагаемых, каждая из которых соответствует определенному виду ионов. Это соотношение установлено Кольраушем и называется законом независимого движения ионов (законом Кольрауша): эквивалентная электропроводность при бесконечном разведении равна сумме предельных подвижностей ионов. Сущность этого закона состоит в следующем: в предельно разбавленном растворе электролита катионы и анионы переносят ток независимо друг от друга.
Закон Кольрауша помог вычислить значения λ ∞ для многих слабых электролитов, для которых нельзя было определить эти значения из опытных данных экстрополяцией их к нулевой концентрации (или к бесконечному разведению) как это делается в случае сильных (и средних) электролитов. Предельные подвижности ионов, как и эквивалентная электропроводность, увеличиваются с температурой. Их значения, например, при 25 оС лежат в интервале от 30 до 80 и от 40 до 80 (см2·Oм‑ 1·моль-экв-1) для однозарядных катионов и анионов соответственно.
У ионов ОН ‑ и Н + наблюдается аномально высокие подвижности:
 198 и
198 и 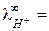 350 (см2× Ом-1 моль-экв-1) при 25 оС,
350 (см2× Ом-1 моль-экв-1) при 25 оС,
что объясняется особым — эстафетным — механизмом их перемещения (рис. 4).
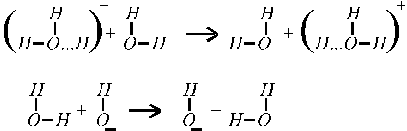 |
Рис. 4. Эстафетный механизм перемещения ионов ОН - и Н +.
На основании эквивалентной электропроводности раствора электролита и предельных подвижностей ионов можно рассчитать степень диссоциации слабого электролита:
 , (2.18).
, (2.18).
Для сильных электролитов, диссоциирующих полностью, рассчитывают 
коэффициент электропроводности:
 , (2.19)
, (2.19)
который учитывает влияние электростатического взаимодействия ионов на скорость их движения.
С учётом нового понятия ‑ подвижность иона ‑ для удельной электропроводности можно записать:
æ  , (2.20)
, (2.20)
æ  . (2.21)
. (2.21)
Отметим, что в современной научной и учебной литературе используется также понятие молярной электропроводности λ m, которую легко связать с величиной λ, зная количество моль-эквивалентов (Z) в 1 моле вещества:
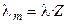 . (2.22)
. (2.22)
2.2. ЗАВИСИМОСТЬ УДЕЛЬНОЙ И ЭКВИВАЛЕНТНОЙ ЭЛЕКТРОПРОВОДНОСТЕЙ ОТ КОНЦЕНТРАЦИИ
ДЛЯ СЛАБЫХ И СИЛЬНЫХ ЭЛЕКТРОЛИТОВ.
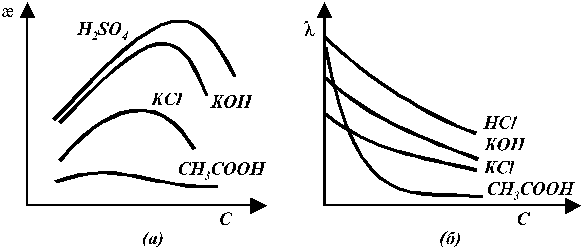 |
Эквивалентная электропроводность слабых и сильных электролитов увеличивается с разбавлением (рис. 5 б). Для слабых электролитов это обусловлено в основном тем, что с увеличением разведения степень диссоциации электролита возрастает и в пределе стремится к 1. Рост эквивалентной электропроводности сильных электролитов связан в основном с изменением подвижностей ионов. Подвижность ионов тем меньше, чем больше концентрация раствора. В области сильно разбавленных растворов подвижности ионов достигают своего предельного значения.
Рис. 5. Зависимость удельной (а) и эквивалентной (б)
электропроводности от концентрации раствора электролита.
Удельная электропроводность для сильных электролитов тем выше, чем больше концентрация ионов и чем больше их абсолютные скорости (подвижности). Наибольшей удельной электропроводностью обладают кислоты, затем основания, далее идут соли, очень мала электропроводность растворов таких слабых электролитов, как уксусная кислота или аммиак.
Кривые зависимостей удельной электропроводности от концентрации имеют максимумы (рис. 5 а). В разбавленных растворах слабых и сильных электролитов рост удельной электропроводности с концентрацией обусловлен увеличением числа ионов, переносящих электричество. Дальнейшее увеличение концентрации сопровождается увеличением вязкости раствора, что снижает скорость движения ионов и электропроводность. Более того, у слабых электролитов в концентрированных растворах заметно снижается степень диссоциации и, следовательно, общее число ионов. Для слабых электролитов скорость движения ионов почти не зависит от концентрации и в общем случае их удельная электропроводность изменяется с концентрацией незначительно.
Для сильных электролитов в области разбавленных растворов межионные взаимодействия практически отсутствуют, но число ионов невелико — удельная электропроводность мала. С увеличением концентрации увеличивается число ионов в единице объёма, что приводит к росту удельной электропроводности. Однако в дальнейшем усиливающееся взаимодействие между ионами приводит к снижению подвижности ионов и рост электропроводности замедляется. Наконец, взаимодействие между ионами с ростом концентрации начинает увеличиваться настолько сильно, что приводит к уменьшению удельной электропроводности.
С позиций теории Дебая-Гюккеля уменьшение подвижности ионов с ростом концентрации обусловлено эффектами торможения движения ионов за счёт электростатического взаимодействия между ионом и ионной атмосферой.
Эффект электрофоретического торможения обусловлен торможением движения центрального иона встречным движением ионной атмосферы и имеет гидродинамическую природу. Поскольку ионы гидратированы, то движение центрального иона происходит не в неподвижной среде, а в среде, перемещающейся ему навстречу. Движущийся ион находится под влиянием дополнительной тормозящей силы (силы электрофоретического торможения), что приводит к снижению скорости его движения.
Эффект релаксационного торможения. Ионная атмосфера обладает сферической симметрией до тех пор, пока отсутствует внешнее электрическое поле. Как только центральный ион начинает движение под действием электрического поля, симметрия ионной атмосферы нарушается. Перемещение иона сопровождается разрушением ионной атмосферы в обном положении иона и формированием ее в ругом, новом. Этот процесс происходит с конечной скоростью в течение некоторого времени, называемого временем релаксации. В результате ионная атмосфера теряет центральную симметрию и позади движущегося иона всегда будет находиться некоторый избыток заряда противоположного знака, что и вызывает уменьшение его скорости движения.
Плотность ионной атмосферы увеличивается с ростом концентрации электролита, что приводит к усилению эффектов торможения. Теория электрофоретического и релаксационного эффектов была разработана Л. Онзагером. Она количественно позволяет учесть влияние этих эффектов на величину эквивалентной электропроводности раствора электролита:
 , (2.23)
, (2.23)
где постоянные (В 1·λ ∞ ) и В 2 характеризуют влияние релаксационного и электрофоретического эффектов соответственно. В растворах с С → 0 эти эффекты практически не проявляются и  .
.
2.4. ЭКСПЕРИМЕНТАЛЬНЫЕ ПРИЛОЖЕНИЯ МЕТОДА ЭЛЕКТРОПРОВОДНОСТИ.
2.4.1. Определение константы диссоциации и степени диссоциации
слабых электролитов.
Степень диссоциации a слабого электролита может быть найдена из соотношения (8.18):
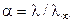 .
.
Константа диссоциации КД слабого электролита связана со степенью диссоциации a уравнением
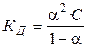 . (2.24)
. (2.24)
С учетом (8.18), получаем
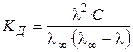 . (2.25)
. (2.25)
Величина λ ∞ рассчитывается по закону Кольрауша (уравнение 2.17).
2.4.2. Определение произведения растворимости
малорастворимых соединений.
Растворимостью электролита (S) называется его концентрация в насыщенном растворе (моль/л), а произведением растворимости (ПР) – произведение активностей катиона и аниона труднорастворимой соли.
Насыщенный раствор малорастворимой соли является очень разбавленным раствором (α → 1 и λ → λ ∞ ). Тогда
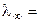 (æ ·1000) / C. (2.26)
(æ ·1000) / C. (2.26)
Найдя значение λ ∞ по табличным данным и измерив удельную электропроводность раствора, можно вычислить концентрацию насыщенного раствора (в моль-экв/л), которая представляет собой растворимость соли
C = (æ ·1000) / λ ∞ = S (2.27).
Поскольку æ малорастворимых растворов (æ Р) часто соизмерима с электропроводностью воды (æ В), то в уравнениях удельная электропроводность раствора часто рассчитывается как разность: æ = æ Р – æ В.
Для труднорастворимых солей активности катиона и аниона практически совпадают с их концентрациями, поэтому
ПР = 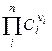 (2.28),
(2.28),
где ni – стехиометрический коэффициент иона в уравнении диссоциации; n – число видов ионов, на которые диссоциирует электролит; Ci – концентрация иона, связанная с концентрацией электролита С соотношением
 .
.
Так как a = 1, то
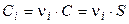 ,
,
и произведение растворимости
 . (2.29)
. (2.29)
Так, для малорастворимого (бинарного) одно–одновалентного электролита, диссоцииирующего по схеме
 ,
,
получим
 (моль/л)2.
(моль/л)2.
ТЕМА 3
Электродные процессы. Понятие об электродвижущих силах (ЭДС) и скачках потенциалов. Электрохимические цепи, гальванические элементы. Нормальный водородный электрод, стандартный электродный потенциал. Термодинамика гальванического элемента. Классификация электрохимических цепей и электродов.
3.1. ЭЛЕКТРОхимические системы. Электрод.
Электрохимический потециал. Абсолютные
Электродные потенциалы и ЭЛЕКТРОДВИЖУЩая СИЛА.
Взаимное превращение электрической и химической форм энергии происходит в электрохимических системах, состоящих из следующих частей:
1. Проводники второго рода, обладающие ионной проводимостью (электролиты).
2. Проводники первого рода – вещества, обладающие электронной проводимостью, находящиеся в контакте с электролитом. На границе раздела двух фаз происходит перенос электрического заряда, т.е. протекает электрохимическая реакция. Такая система, состоящая из проводников первого и второго рода, называется электродом.
3. Проводники, обеспечивающие прохождение тока между электродами.
Химические превращения, которые происходят в растворах или расплавах на электродах из проводников первого рода, называются электродными процессами. Эти процессы можно разделить на две группы, тесно связанные друг с другом. Во-первых, это возникновение разности потенциалов и электрического тока в гальванических элементах. Во-вторых, обратные им химические процессы, которые имеют место при прохождении постоянного электрического тока через раствор или расплав, называемые электролизом.
Электрод представляет собой систему, состоящую как минимум из двух фаз. Характерная особенность электрохимической системы заключается в том, что вещества, учавствующие в суммарной токообразующей реакции, пространственно разделены. Поэтому реакция распадается на две частные реакции, каждая из которых совершается на отдельном электроде. Состояние заряженной частицы в фазе определяется электрохимическим потенциалом
 , (3.1)
, (3.1)
где zi – заряд иона, g – внутренний потенциал, отвечающий работе переноса элементарного отрицательного заряда из бесконечности в вакууме вглубь фазы. Равновесие электрохимической системы характеризуется равенством электрохимических (а не химических) потенциалов заряженных частиц в различных фазах.
Рассмотрим, как возникает скачок потенциала – электродный потенциал — на границе границе раздела металл–раствор. При погружении металлической пластинки в воду некоторая часть ионов металла с поверхности пластинки в результате взаимодействия с молекулами воды переходит в раствор, прилегающий к поверхности пластинки. Металл заряжается отрицательно, и возникающие электростатические силы препятствуют дальнейшему протеканию этого процесса. В системе устанавливается равновесие. Указанные процессы приводят к возникновению двойного электрического слоя и скачка потенциала между отрицательно заряженной пластинкой и слоем положительно заряженных ионов в растворе. Толщина двойного электрического слоя в разбавленных растворах составляет сотни ангстрем, а в концентрированных уменьшается до нескольких ангстрем.
Для ионов, находящихся в равновесной системе растворI/электродII, имеем:
 . (3.2)
. (3.2)
Работа перенесения иона из фазы I в фазу II равна
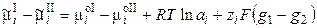 , (3.3)
, (3.3)
так как
 (3.4)
(3.4)
В равновесии  , следовательно,
, следовательно,
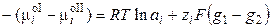 , (3.5)
, (3.5)
 , (3.6)
, (3.6)
где φ – абсолютный электродный потенциал, т.е. скачок потенциала между двумя фазами. Обозначим
 ,
,
где φ о ‑ стандартный электродный потенциал (скачок потенциала на границе раздела фаз при аi = 1). Стандартный потенциал представляет собой величину, характерную для данного электродного процесса, и зависит от температуры и природы растворителя. Тогда
 . (3.7)
. (3.7)
Уравнение (3.7) называют уравнением Нернста для электродного потенциала. Разность внутренних потенциалов иона в двух фазах (g 2 – g 1) компенсирует разность химических потенциалов иона. Разность электрических потенциалов экспериментально можно измерить только между двумя точками одной и той же системы (μ i = const), поэтому электродный потенциал нельзя измерить абсолютно, только относительно.
Разность потенциалов между электродами зависит от условий (температуры, природы металлов, активности ионов в растворе), в которых она определяется. Эта разность максимальна при равновесных условиях работы электрохимической системы, при которых внешнее сопротивление бесконечно велико, а ток в цепи – бесконечно мал. Такая разность потенциалов получила название электродвижущей силы (ЭДС).
3.2. Правила записи электродов и электрохимических цепей.
Уравнение Нернста для ЭДС электрохимической цепи.
Системы, состоящие из двух и более электродов, способные производить электрическую работу, т. е. служить источником электрической энергии, называются электрохимическими цепями (системами). Электрохимическая система, состоящая из двух электродов, в которой химическая энергия протекающей суммарной реакции превращается в электрическую работу называется гальваническим элементом.
3.2.1. Правила записи электродов и электрохимических цепей.
Для электродов (полуэлементов): вещества, находящиеся в растворе, указываются слева от вертикальной черты, справа указываются вещества, образующие другую фазу, или электродный материал. Если одна фаза содержит несколько веществ, то их символы разделяются запятыми. Например,
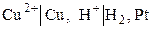 .
.
Уравнение электродной реакции записывается так, чтобы слева располагались вещества в окисленной форме и электроны, справа – вещества в восстановленной форме:
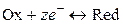 ,
,
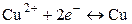 ,
,
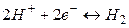 .
.
Для электрохимических цепей: слева располагается электрод, имеющий более отрицательный потенциал; растворы обоих электродов отделяются друг от друга вертикальной пунктирной линией, если они контактируют друг с другом, и двумя сплошными линиями, если между растворами находится солевой мостик, с помощью которого устраняется диффузионный потенциал:
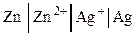 .
.
Справа всегда указывается положительно заряженный электрод, слева – отрицательно заряженный.
В качестве примера электрохимической цепи, используемой на практике для получения электрической энергии, рассмотрим гальванический элемент, состоящий из серебряного и медного электродов, которые погружены соответственно в растворы AgNO3 и CuSO4. Схематически рассматриваемый элемент записывается в следующем виде:
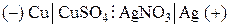 , (I)
, (I)
где вертикальная линия обозначает поверхность раздела металл–раствор, а вертикальная пунктирная – поверхность раздела раствор–раствор.
В результате работы элемента на медном электроде будут образовываться и переходить в раствор ионы меди (процесс окисления):
 , (II)
, (II)
а на серебряном электроде будут разряжаться ионы серебра и осаждаться металлическое серебро (процесс восстановления):
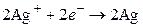 . (III)
. (III)
Процессы окисления и восстановления в гальваническом элементе протекают раздельно.
Электрод, на котором протекает процесс окисления (II), называется анодом и в гальваническом элементе заряжен отрицательно. Электрод, на котором протекает процесс восстановления (III), заряжен положительно и называется катодом. Реакции (II) и (III) называются электродными реакциями.
Суммарный химический процесс, протекающий в элементе (I), слагается из отдельных процессов у электродов и выражается уравнением:
 . (IV)
. (IV)
Если электродные процессы и химическая реакция в гальваническом элементе могут быть осуществлены в прямом (при работе элемента) и обратном (при пропускании электрического тока через элемент в противоположном направлении) направлениях, то такие электроды и гальванический элемент носят название обратимых. В частности гальванический элемент (I) можно отнести к обратимым элементам. При его работе протекают электродные процессы (II) и (III). При пропускании же через него электрического тока в обратном направлении на медном электроде будут разряжаться ионы Cu2+ и выделяться металлическая медь, а на серебряном электроде – образовываться и переходить в раствор ионы Ag+. В этом случае электрохимическая реакция (IV) будет протекать справа налево. Примером необратимого электрода может быть, например, медь в растворе кислоты. В дальнейшем будут рассматриваться только обратимые гальванические элементы.
3.2.2. Уравнение Нернста для ЭДС гальванического элемента.
Электрической характеристикой электрода является потенциал, а гальванического элемента (электрохимической цепи) ‑ электродвижущая сила (ЭДС), равная алгебраической сумме скачков потенциала, возникающих на границе раздела фаз, входящих в состав цепи. ЭДС электрохимической цепи соответствует разности потенциалов правого (положительного) и левого (отрицательного) электродов и всегда положительна.
ЭДС гальванического элемента (I) равна:
 (3.8)
(3.8)
где  и
и 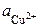 – активности ионов Ag+ и Cu2+ в растворах их солей. Обозначим
– активности ионов Ag+ и Cu2+ в растворах их солей. Обозначим
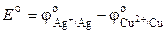 , (3.9)
, (3.9)
где Е о – стандартная ЭДС гальванического элемента. Тогда
 . (3.10)
. (3.10)
Следует помнить, что активность чистого твердого вещества принимается равной единице. Уравнение (3.8) носит название уравнения Нернста для ЭДС гальванического элемента.
Пусть в гальваническом элементе протекает обратимая химическая реакция
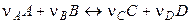 .
.
Максимальная полезная работа гальванического элемента при стандартных условиях равна
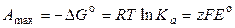 , (3.11)
, (3.11)
где z – число электронов, участвующих в элетродных реакциях (одинаковое для обоих электродов), F – постоянная Фарадея.
По уравнению изотермы Вант-Гоффа
 , (3.12)
, (3.12)
или
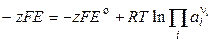 . (3.13)
. (3.13)
Следовательно,
 . (3.14)
. (3.14)
Уравнение Нернста в форме (3.14) применимо для расчета ЭДС любого гальванического элемента (по суммарной химической реакции) и потенциала любого электрода (по электродной реакции
3.3. Стандартный ВОДОРОДНЫЙ ЭЛЕКТРОД.
ЭЛЕКТРОДНЫЙ ПОТЕНЦИАЛ.
Можно с высокой точностью измерить ЭДС цепи, составленной из двух электродов. Однако нельзя ни измерить, ни вычислить абсолютную разность потенциалов φ на границе металл–раствор. Для практических целей достаточно иметь условные величины, характеризующие потенциалы различных электродов, отнесенные к потенциалу некоторого электрода, выбранного за стандартный.
В качестве условно-нулевого потенциала выбран потенциал стандартного водородного электрода:
 ,
,
в котором давление продуваемого водорода равно 1 атм, а активность ионов водорода в растворе равна 1 (рис. 7).
Электродная реакция
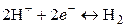 .
.
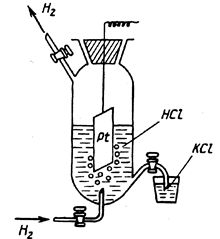
Рис. 7. Общий вид водородного электрода.
Потенциал стандартного водородного электрода равен
 ,
,
С учетом того, что 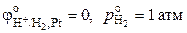 , R = 8.314 Дж·моль-1·К-1, F = 96485 Кл·моль-экв-1, и заменяя натуральный логарифм десятичным, получаем
, R = 8.314 Дж·моль-1·К-1, F = 96485 Кл·моль-экв-1, и заменяя натуральный логарифм десятичным, получаем
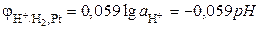 .
.
Электродным потенциалом любого другого электрода называют его потенциал по отношению к стандартному водородному. Другими словами, за электродный потенциал принимают ЭДС цепи, составленной из рассматриваемого электрода и стандартного водородного электрода. При этом справа в цепи расположен рассматриваемый электрод, а слева – стандартный водородный электрод. ЭДС положительна (электродный потенциал положителен), если электрический ток внутри цепи течёт слева направо, и отрицательна – если наоборот.
Пример 3.1.
1) Составим гальванический элемент из платинового и медного электродов:
 .
.
Суммарная токообразующая реакция: 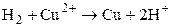 , т.е. перенос электронов в цепи происходит слева направо (от левого электрода к правому). При стандартных условиях (
, т.е. перенос электронов в цепи происходит слева направо (от левого электрода к правому). При стандартных условиях ( )
)  .
.
2) Составим гальванический элемент из платинового и цинкового эдектродов:
 .
.
Суммарная реакция: 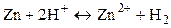 , т.е. перенос электронов в цепи происходит справа налево. При стандартных условиях (
, т.е. перенос электронов в цепи происходит справа налево. При стандартных условиях ( )
)  .
.
Следует помнить, что ЭДС цепи всегда положительна, поэтому рассматриваемый гальванический элемент следует записать в следующем виде:
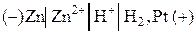 ,
,
при стандартных условиях 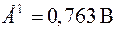 .
.
3.4. ТЕРМОДИНАМИКА ГАЛЬВАНИЧЕСКОГО ЭЛЕМЕНТА.
Гальванический элемент при работе в условиях тепловой изоляции нагревается или охлаждается. Поэтому можно предположить, что источником совершаемой электрической работы являются тепловой эффект химической реакции и энергия окружающей среды.
Рассмотрим уравнение Гиббса-Гельмгольца в следующей форме:
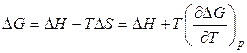 , (3.15)
, (3.15)
где Δ Н и Δ S – тепловой эффект и энтропия химической реакции, протекающей в гальваническом элементе. Максимальная полезная работа электрохимической цепи равна убыли энергии Гиббса:
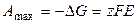 , (3.16)
, (3.16)
 . (3.17)
. (3.17)
Тогда:
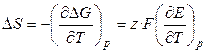 , (3.18)
, (3.18)
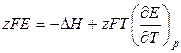 , (3.19)
, (3.19)
 , (3.20)
, (3.20)
 , (3.21)
, (3.21)
Следовательно,
 , если
, если 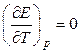 ,
,
т.е. в этом случае вся электрическая работа цепи производится за счет теплового эффекта химической реакции. Если
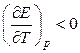 , то
, то 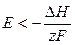 ,
,
т. е. электрическая работа меньше теплового эффекта реакции. Гальванический элемент при изотермических условиях отдает теплоту в окружающую среду или нагревается в условиях тепловой изоляции. Если
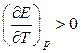 , то
, то  ,
,
т. е. электрическая работа больше теплового эффекта реакции. Гальванический элемент при изотермических условиях поглощает теплоту из окружающей среды или охлаждается в условиях тепловой изоляции.
Измерение ЭДС обратимых гальванических элементов при различных температурах позволяет определить термодинамические характеристики химических реакций, протекающих в них, по уравнениям (3.16), (3.18) и (3.20).
3.5. КЛАССИФИКАЦИЯ ЭЛЕКТРОХИМИЧЕСКИХ ЦЕПЕЙ.
Гальванические элементы классифицируют по двум признакам:
1. По характеру суммарного процесса, лежащего в основе действия гальванического элемента. Это или химическая реакция, или процесс выравнивания концентраций двух растворов одного и того же электролита. По этому признаку элементы делятся на химические и концентрационные.
1.1. Концентрационные цепи. Концентрационные электрохимические цепи состоят из электродов с одинаковыми потенциалопределяющими реакциями. Физические и химические свойства материала электродов одинаковы, но активности одного (или нескольких) участников реакции на каждом из электродов различны. ЭДС цепи определяется отношением активностей (по уравнению Нернста):
 ,
, 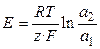 .
.
В уравнение Нернста для ЭДС цепи не входят стандартные электродные потенциалы, так как они одинаковы. По результатам измерений ЭДС такой цепи и известной активности компонента в одном электроде можно рассчитать активность компонента в другом электроде. Примером концентрационной цепи может служить следующий гальванический элемент (а 2 > a 1): 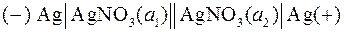 .
.
1.2. Химические цепи. Химические цепи состоят из электродов, потенциалопределяющие реакции которых различны. Электроды в таких системах отличаются и по физическим, и по химическим свойствам. Электрическая энергия возникает за счет энергии суммарной химической реакции, для которой справедливы ранее установленные соотношения между ЭДС и тепловым эффектом реакции, а также между стандартной ЭДС и константой равновесия реакции. Химические цепи разнообразны по природе и свойствам электродов, из которых они состоят. Примером такой цепи может служить серебряно-цинковый элемент:  .
.
Чтобы решить вопрос о направлении суммарной химической реакции, протекающей в элементе, прежде всего следует определить полярности электродов. Катодом (положительно заряженным, правым) всегда является электрод с более положительным потенциалом. Так как
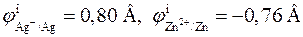 ,
,
то в стандартных условиях серебряный электрод будет катодом, а цинковый электрод ‑ анодом. Стандартная ЭДС элемента равна
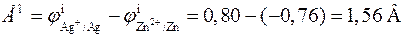 .
.
Уравнения потенциалопределяющих реакций:
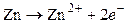 ,
, 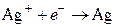 .
.
Суммарная реакция в цепи

электронейтральна (электродные реакции уравнены по числу электронов и участвующих в них веществ). ЭДС элемента по уравнению Нернста равна
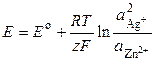 .
.
Важным частным случаем химических цепей являются цепи, в которых хотя бы один из электродов является окислительно–восстановительным. Электрический ток в таких цепях возникает за счет реакций окисления и восстановления, протекающих в растворе. Примером такой цепи является цепь, составленная из стандартного водородного электрода и железного окислительно–восстановительного (редокс) электрода:
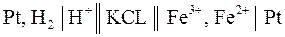 .
.
2. По наличию или отсутствию жидкостного соединения между двумя растворами гальванического элемента. По этому признаку элементы делят на цепи с переносом и цепи без переноса ионов.
2.1. Цепь с переносом – это цепь с жидкостной границей. Например, цепь вида
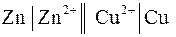 .
.
В состав цинкового и медного электродов входят растворы различной природы. Контакт между двумя растворами обеспечивается с помощью специальных приспособлений, например, солевым мостиком, состоящим из трубки, заполненной смесью влажного желеобразного вещества агар-агара с солью сильного электролита (КСl). Диффузионный потенциал на границе раздела раствор-раствор элиминирован.
2.2. Цепь без переноса – это цепь без жидкостной границы. Например, цепь вида
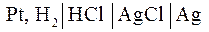 ,
,
в которой оба электрода погружены в один и тот же раствор.
3.6. КЛАССИФИКАЦИЯ Обратимых ЭЛЕКТРОДОВ.
Классификация обратимых электродов основана на свойствах веществ, участвующих в потенциалопределяющих процессах.
3.6.1. Электроды первого рода.
Это металлические электроды, обратимые относительно катионов (в том числе амальгамные) и металлоидные, обратимые относительно анионов (например, Se2-/Se). В таких электродах восстановленной формой является металл, а окисленной – ион этого металла.
Если электрод обратим относительно катиона, то
 ,
, 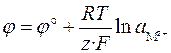 .
.
Если электрод обратим относительно аниона, то
 ,
,  .
.
К электродам первого рода относятся также газовые электроды (водородный, кислородный, хлорный). Они могут