
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА 10. Основные понятия химической кинетики
|
|
Основные понятия химической кинетики. Кинетика необратимых гомогенных простых реакций. Методы определения порядка реакции. Влияние температуры на скорость реакции. Кинетика сложных реакций.
4.1. ОСНОВНЫЕ ПОНЯТИЯ ХИМИЧЕСКОЙ КИНЕТИКИ.
Химическая кинетика — раздел физической химии, который устанавливает законы, определяющие скорость химических процессов, и выясняет роль различных факторов, влияющих на скорость и механизм реакций.
Рассмотрим реакцию
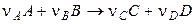 , (4.1)
, (4.1)
где А и В — исходные вещества, С и D — продукты реакции; ν — стехиометрические коэффициенты. Поскольку в реакции участвует несколько веществ, то можно говорить как о скорости реакции в целом, так и о скорости реакции по данному веществу. Скоростью реакции по данному веществу i называется изменение числа молей i -го вещества в единице объема за единицу времени:
 (4.2)
(4.2)
Если объем системы не изменяется или мало изменяется в ходе реакции (V = const), что характерно для большинства реакций, протекающих в растворах, то
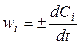 , (4.3)
, (4.3)
где Сi = (ni / V) — молярная концентрация i -вещества в растворе.
В процессе реакции концентрация исходных веществ уменьшается (dC i /dt < 0), а концентрация продуктов реакции увеличивается (dCi /dt > 0). Так как скорость реакции всегда величина положительная, то в уравнениях для скорости реакции (4.2) и (4.3) знак “+” относится к продуктам реакции, а знак “‑ ” к исходным веществам.
Скорость реакции в целом равна скорости реакции по данным веществам, деленным на соответствующие стехиометрические коэффициенты, то есть для реакции (4.1)
 .
.
В химической кинетике также различают
1) истинную (или мгновенную) скорость реакции в момент времени t, равную w = ± dC/dt,
2) среднюю скорость реакции за промежуток времени D t, равную w = ±D C/ D t.
Если реакция является простой, то есть протекает в одну стадию (одностадийная реакция), то зависимость скорости реакции от концентрации веществ определяется законом действующих масс, который часто называют основным постулатом кинетики: “Скорость одностадийной химической реакции пропорциональна концентрации реагирующих веществ, возведенных в степени, равные их стехиометрическим коэффициентам в уравнении реакции”. Тогда для скорости прямой реакции (4.1) можно записать
 , (4.4)
, (4.4)
где k — константа скорости реакции, не зависящая от концентрации реагирующих веществ. Физический смысл константы скорости состоит в том, что она равна скорости химической реакции при единичных концентрациях всех реагирующих веществ (например, C A = C B = 1 моль/л).
Однако практически все реакции в природе являются сложными, т.е. состоят из совокупности элементарных процессов (или стадий), идущих последовательно или параллельно. Скорость сложных реакций зависит от концентрации исходных, промежуточных веществ, а иногда и от концентрации продуктов реакции и инертных веществ. Поэтому выражение для скорости сложной реакции в виде (4.4) всегда находят опытным путем.
В общем случае для прямой реакции (4.1) можно записать
 , (4.5)
, (4.5)
где n 1 — порядок реакции по веществу А, n 2 — порядок реакции по веществу В (кинетический или опытный порядок реакции по веществу определяется как показатель степени n, в которой концентрация этого вещества входит в выражение для скорости реакции, полученное опытным путем). Общий порядокреакции равен сумме порядков по веществам, т.е. n = n 1 + n 2. Величины n 1 и n 2 совпадают со стехиометрическими коэффициентами только для простых реакций. Для сложных реакций n 1 ¹ ν А и n 2 ¹ ν B.
Под молекулярностью реакции (стадии) понимается число частиц, участвующих в элементарной стадии реакции. В отличие от порядка реакции, это теоретическое понятие. Молекулярность реакции — всегда целое число (а порядок реакции может быть целым, дробным или даже отрицательным).
Различают моно-, би- и тримолекулярные реакции, например:
Cl2 ® Cl + Cl (моно-),
HI + HI ® H2 + I2 (би-),
H + H + M ® H2 + M (три-), где М — третья частица.
Порядок и молекулярность реакции совпадают только для простых реакций или элементарных стадий сложных реакций. Например, реакция взаимодействия оксида азота (II) с хлором является сложной, протекает в две стадии, обе стадии являются бимолекулярными:
2NO + Cl2 ® 2NOCl
1) NO + Cl2 ® NOCl2,
2) NOCl2 + NO ® 2NOCl.
4.2. КИНЕТИКА НЕОБРАТИМЫХ ГОМОГЕННЫХ ПРОСТЫХ РЕАКЦИЙ.
Рассмотрим необратимые гомогенные простые реакции нулевого, первого и второго порядков (с точки зрения формальной кинетики необратимыми являются такие реакции, для которых через некоторое время с начала их протекания концентрации исходных веществ не удается обнаружить аналитическими методами).
4.2.1. Реакции нулевого порядка.
Для реакций нулевого порядка (чаще всего гетерогенных реакций) скорость реакции постоянна и не зависит от концентрации исходных веществ. Например, для реакции А ® B
 . (4.6)
. (4.6)
Разделим переменные в уравнениии (10.6) и проинтегрируем его
 ,
,
где С 0 — начальная концентрация вещества А в начальный момент времени t = 0, С — концентрация А в момент времени t (текущая концентрация А). Результирующее уравнение, описывающее зависимость концентрации вещества А от времени, имеет вид:
С = С 0 - k 0 t, (4.7)
или
 .
.
Размерность k 0 — [концентрация·время‑ 1]. Если концентрация выражена в моль/л, а время — в сек, то k 0 выражается в моль/(л·сек).
Время, в течение которого концентрация исходного вещества уменьшается в два раза, называется периодом (временем) полупревращения и обозначается t 1/2. Для реакции нулевого порядка
 ,
,
т.е. время полупревращения прямо пропорционально начальной концентрации вещества (при увеличении С 0 в 2 раза, t 1/2 увеличивается в 2 раза).
Зависимость текущей концентрации вещества А от времени имеет линейный вид и представлена на рис. 1(а). Реакции нулевого порядка имеют место в тех случаях, когда убыль вещества в результате протекания химической реакции восполняется доставкой его из другой фазы. Нулевой порядок наблюдается также, если скорость процесса лимитируется подачей энергии, необходимой для активации реагирующих молекул.
10.2.2. Реакции первого порядка.
Рассмотрим реакцию первого порядка А ® В. Скорость этой реакции описывается уравнением
 |
 . (4.8)
. (4.8)
Рис. 1. К расчету константы скорости реакции нулевого (а) и первого (б) порядков.
Разделим переменные в уравнении (4.8) и проинтегрируем его
 ,
,
где С 0 — начальная концентрация вещества А в начальный момент времени t = 0, С — текущая концентрация А в момент времени t. Результирующее уравнение, описывающее зависимость концентрации вещества А от времени, имеет вид:
ln C = ln C 0 - k 1 t, (4.9)
или
 ,
,  ,
,
т. е. концентрация вещества А в ходе реакции уменьшается экспоненциально.
Размерность константы скорости первого порядка — [время-1]:
 [напр., сек-1 или мин-1]. (4.10)
[напр., сек-1 или мин-1]. (4.10)
Время полупревращения для реакции первого порядка не зависит от начальной концентрации вещества:
 .
.
Зависимость логарифма концентрации вещества А от времени имеет линейный вид, что следует из ур-я (10.9), и представлена на рис. 1(б). К числу односторонних реакций первого порядка относятся реакции радиоактивного распада, реакции разложения сложных веществ (карбонатов, кристаллогидратов) при их нагревании, реакции изомеризации.
Пример 4.1. За 14 дней активность Ро210 уменьшилась на 6, 85%. Определить значение константы скорости реакции первого порядка и период полураспада t 1/2.
Решение. Из условий задачи N 1 = 0, 9315· N 0, поэтому
 дней
дней  .
.
Тогда
 дней.
дней.
10.2.3. Реакции второго порядка.
Рассмотрим реакцию второго порядка А + В ® D. Скорость этой реакции описывается уравнением
 . (4.11)
. (4.11)
Если начальные концентрации веществ А и В равны (С 0А = С 0В = С 0), тогда текущие концентрации этих веществ также будут равны (СА = СВ = С). Результирующее уравнение, описывающее зависимость концентрации веществ от времени, имеет вид
 . (4.12)
. (4.12)
Размерность костанты скорости второго порядка — [концентрация-1·время-1]. Если концентрация выражена в моль/л, а время — в сек, то
 [л/(моль·сек)]. (4.13)
[л/(моль·сек)]. (4.13)
Время полупревращения для реакции второго порядка обратно пропорционально начальной концентрации веществ:
 .
.
(Аналогичные уравнения для константы скорости и времени полупревращения получаются для бимолекулярных реакций типа 2 А ® D).
Зависимость обратной концентрации вещества А от времени имеет линейный вид, что следует из уравнения (10.13), и представлена на рис. 2.
В случае реакции А + В ® D, если начальные концентрации реагирующих веществ не равны (С 0А ¹ С 0В), результирующее уравнение принимает следующий вид:
 , (4.14)
, (4.14)
где СА и СВ — текущие концентрации веществ А и В в момент времени t.
 |
Рис. 2. К расчету константы скорости реакции второго порядка.
4.3. МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОРЯДКА РЕАКЦИИ.
На практике исследование скорости химических реакций начинают с определения порядков этой реакции по каждому из реагирующих веществ и (или) порядка реакции в целом. Существуют следующие методы определения порядка реакции.
4.3.1. Метод подстановки в формулы.
Заключается в том, что опытные результаты (текущие концентрации веществ в моменты времени t) последовательно подставляются в интегральные кинетические уравнения реакций нулевого (ур-е 4.7), первого (ур-е 4.10), второго (ур-е 4.13 или 4.14) порядков и определяется, какое из уравнений дает практически постоянную величину константы скорости. Именно это уравнение и определяет порядок исследуемой реакции.
10.3.2. Графический метод.
 |  | ||
Он состоит в построении графиков, выражающих зависимость различных функций концентрации от времени, и определения, для какой из них наблюдается прямолинейная
зависимость. Это уравнение и определяет порядок исследуемой реакции.
Рис. 3. Линейные зависимости различных Рис. 4. Определение порядка реакции
функций концентрации реагирующего по зависимости времени полупревращения
вещества от времени. от начальной концентрации.
Линейные зависимости для реакций различных порядков получаются в следующих координатах (рис. 3): нулевого порядка — С = f (t), первого порядка — ln С = f (t), второго порядка — 1/ С = f (t), третьего порядка — 1/ С 2 = f (t).
10.3.3. По времени полупревращения.
Порядок реакции определяется на основе опытной зависимости времени полупревращения (t 1/2) от начальной концентрации вещества (C 0). Если провести реакцию при различных начальных концентрациях С 01 и С 02 и определить периоды полупревращения для этих двух случаев t 1/2(1) и t 1/2(2), то порядок реакции можно рассчитать по формуле:
 .
.
Более точно этим методом можно определить порядок реакции графически, если известны несколько значений t 1/2 при нескольких начальных концентрациях. При построении графика по оси ординат откладываются значения ln(t 1/2), а по оси абсцисс — значения ln C 0 (рис. 4), тогда n = -tga + 1.
В том случае, когда реакция имеет целочисленный порядок и начальные концентрации реагирующих веществ равны, следует помнить, что при С = С 0/2 интегральные кинетические уравнения принимают вид:
 (при n = 0),
(при n = 0),  (при n = 1),
(при n = 1),  (при n = 2).
(при n = 2).
10.3.4. Дифференциальный метод Вант-Гоффа.
Этот метод применяют, когда в реакции участвует одно вещество, или при участии нескольких веществ, когда все вещества, кроме данного (А), взяты в большом избытке. Тогда скорость реакции равна
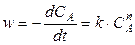 . (4.15)
. (4.15)
Прологарифмировав ур-е (4.15), получим
ln w = ln k + n ln С 
 |  | ||
Построив зависимость ln w от ln C (рис. 5), можно определить порядок реакции, равный в данном случае тангенсу угла наклона прямой (n = tga).
Рис. 5. Определение порядка реакции Рис. 6. Определение скорости реакции
дифференциальным методом Вант-Гоффа. по кинетическим кривым
методом касательных.
Истинные скорости реакции w = -dC/dt можно найти или графическим дифференцированием кинетических кривых (т.е. зависимостей концентраций реагирующих веществ от времени) (рис. 6), или заменив их на средние скорости w = D C /D t.
4.3.5. Метод изоляции или метод избытка.
Если в исследуемой реакции исходных реагирующих веществ более одного (напр., три — А, В, С), то сначала определяют порядок реакции одним из указан-ных выше методов по одному из веществ (А), взяв остальные вещества (В и С) в большом избытке, затем определяют порядок реакции по веществу В, взяв А и С в большом избытке, и т.д. Так, в случае реакции А + В + С ® D ее скорость в общем случае равна
 .
.
Если вещества В и С взяты в большом избытке, то при протекании реакции их концентрации практически не изменяются, т.е.
 .
.
Тогда
 .
.
Определив порядки реакции по каждому из реагирующих веществ, можно найти общий порядок реакции: n = n 1 + n 2 + n 3.
10.4. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ РЕАКЦИИ.
В большинстве случаев скорость реакции с повышением температуры увеличивается. Если при повышении температуры не меняется механизм реакции, то увеличение скорости реакции определяется увеличением константы скорости данной реакции. Для характеристики зависимости скорости химической реакции от температуры было введено понятие температурного коэффициента скорости (γ), равного отношению константы скорости при температуре (Т + 10) к константе скорости при температуре Т (т.е. γ показывает, во сколько раз изменяется константа скорости при увеличении температуры на 10 градусов):
 .
.
Экспериментально было установлено, что повышение температуры на 10 К в области обычных температур (≈ 300 К) увеличивает скорость многих гомогенных реакций в 2 ‑ 4 раза, т. е. для этих реакций γ = (2 ‑ 4). Это правило называется правилом Вант–Гоффа.
В общем случае отношение констант скорости реакции k 2 и k 1, определенных при двух различных температурах Т 2 и Т 1, равно
 .
.
Однако подобная оценка зависимости скорости реакции от температуры является весьма приближенной и эффективна для реакций, протекающих в растворах при относительно низких температурах. При повышении температуры коэффициент γ не остается постоянным (он уменьшается и при высоких температурах стремится к единице).
Более точную зависимость скорости реакции от температуры дает уравнение Аррениуса:
 , (4.16)
, (4.16)
где k — константа скорости реакции, R — универсальная газовая постоянная, Е — энергия активации химической реакции. В случае простых реакций величина Е показывает, какой минимальной (избыточной по сравнению со средней) энергией в расчете на 1 моль должны обладать реагирующие частицы, чтобы они могли вступить в химическую реакцию. В случае сложных реакций величина Е называется эмпирической или кажущейся энергией активации и в общем случае зависит от энергий активации отдельных стадий данной реакции.
Проинтегрировав уравнение (4.16), получим уравнение Аррениуса в интегральной форме:
 , (4.17)
, (4.17)
или
 ,
,
где А — предэкспоненциальный множитель. Физический смысл А в случае простых реакций: мономолекулярных — это частота колебаний по разрываемой связи (А» 1013 сек-1), бимолекулярных — величина А пропорциональна общему числу столкновений между молекулами реагирующих веществ (А» 10-10 ¸ 10-11 см3/(мол-л·сек).
Проинтегрировав ур-е (10.16) в пределах температур от Т 1 до Т 2, получим:
 . (4.18)
. (4.18)
Энергию активации можно определить как аналитически по уравнению (10.18), так и графическим методом. Для этого необходимо знать ряд констант скоростей при разных температурах. Если реакция подчиняется уравнению Аррениуса, то зависимость ln k от 1/ T должна выражаться прямой линией, что следует из уравнения (4.17) (рис. 7).
 |
Рис. 7. К расчету энергии активации реакции
по температурной зависимости константы скорости.
Для очень большого числа реакций энергия активации находится в пределах от 60 до 240 кДж/моль, т.е. примерно соответствует энергиям химических связей.
4.5. КИНЕТИКА СЛОЖНЫХ РЕАКЦИЙ.
В отличие от простых (одностадийных) реакций, уравнение которых совпадает со стехиометрическим уравнением реакции, подавляющее большинство химических реакций является сложными, т.е. протекает через ряд последовательных и (или) параллельных стадий, при этом некоторые стадии протекают с участием промежуточных веществ, не являющихся ни исходными веществами, ни продуктами реакции.
В основе кинетики сложных реакций лежит принцип независимости реакций, согласно которому “если в системе одновременно протекает несколько реакций, то каждая из них независима от остальных и скорость ее прямо пропорциональна произведению концентраций реагирующих веществ”. Этот принцип справедлив для обратимых, параллельных и последовательных реакций. Конечное изменение концентрации данного вещества является результатом всех независимых изменений.
Однако принцип независимости реакций не является таким общим как основной постулат химической кинетики. Он не применим, например, к сопряженным реакциям, в которых одни простые реакции существенно влияют (часто ускоряют) на протекание других реакций.
Рассмотрим некоторые сложные реакции первого порядка.
4.5.1. Обратимые реакции.
Обратимыми называются реакции, в которых наряду с превращением исходных веществ в продукты протекает с заметной скоростью и противоположно направленная реакция превращения продуктов в исходные вещества. В системах, в которых протекают такие реакции, через некоторое время достигается состояние химического равновесия.
Обратимые реакции – это реакции типа:
А 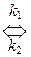 В.
В.
Реакция одновременно протекает как в прямом (константа скорости k 1), так и в обратном (k 2) направлениях. Константа равновесия для обратимой реакции равна
 .
.
Поскольку вещество А расходуется в прямой реакции и образуется в результате обратной, то суммарная скорость изменения концентрации вещества А со временем описывается следующим уравнением
 , (4.19)
, (4.19)
где w 1 и w 2 — скорости прямой и обратной реакций, соответственно; С 0 А — начальная концентрация вещества А (начальная концентрация вещества В равна нулю); СА и СВ — текущте концентрации веществ А и В в момент времени t. В состоянии равновесия w 1 = w 2, тогда
 ,
,
где  — равновесная концентрация вещества В.
— равновесная концентрация вещества В.
10.5.2. Параллельные реакции.
Параллельными называют реакции, в которых одни и те же исходные вещества реагируют одновременно в двух или более направлениях. Это реакции типа
В  А
А  С.
С.
Исходное вещество А одновременно расходуется на образование вещества В (константа k 1) и вещества С (константа скорости k 2). Обе реакции первого порядка. Суммарная скорость расходования вещества А равна
 , (4.20)
, (4.20)
где w 1 и w 2 — скорости превращения вещества А в вещества В и С, соответственно; С 0А — начальная концентрация А; х — количество вещества А, прореагировавшего к моменту времени t.
После интегрирования ур-я (10.20) получаем
 . (4.21)
. (4.21)
По уравнению (10.21) можно рассчитать сумму констант (k 1 + k 2). Чтобы разделить эту сумму на отдельные составляющие, необходимо использовать еще одно уравнение, дающее отношение констант в некоторый момент времени t:
 , (4.22)
, (4.22)
где х 1 и х 2 — числа молей веществ В и С, образовавшихся к моменту времени t (х = х 1 + х 2). Решая систему уравнений (4.21) и (4.22), можно найти значение каждой константы скорости по отдельности.
4.5.3. Последовательные реакции.
Последовательные реакции протекают через ряд стадий, в каждой из которых претерпевает превращение продукт, образовавшийся в предыдущей стадии. К последовательным реакциям относят реакции типа:
А  В
В  D.
D.
Вещество В образуется из А (константа k 1) и расходуется на образование D (константа k 2), обе реакции мономолекулярны. Скорость изменения концентрации вещества В со временем будет равна:
 ,
,
где С 0А — начальная концентрация вещества А (начальные концентрации В и С равны нулю); х и y — число молей веществ А и В, соответственно, прореагировавших к моменту времени t.
4.5.4. Понятие о лимитирующей стадии.
Нередко скорость сложной химической реакции может зависеть главным образом не от всех значений констант скорости отдельных ее стадий, а только от одной. Эту стадию называют лимитирующей (т. е. определяющей скорость всей реакции в целом). Скорость последовательной реакции определяется скоростью наиболее медленной стадии, скорость же параллельных реакций определяется скоростью наиболее быстрой стадии. Например, пусть имеется сложная реакция А ® D, протекающая в три стадии:
А  Р 1
Р 1  Р 2
Р 2  D.
D.
Исходное вещество А превращается в активную промежуточную частицу (АПЧ) Р 1 (константа k 1), которая в свою очередь превращается в АПЧ Р 2 (константа k 2), а уже из Р 2 образуется продукт реакции — вещество D (константа k 3). В том случае, если k 1 < < k 2» k 3, то даже при малых концентрациях Р 1 и Р 2 скорости второй и третьей стадий очень велики и намного превышают скорость первой стадии. Фактически все образовавшееся количество Р 1 очень быстро превращается в продукт реакции D. Скорость всей реакции определяется скоростью образования Р 1 — лимитирующей стадией реакции будут первая:
w @ w 1 = k 1 ·CA.