Лекция Применение производной при нахождении наибольшего и наименьшего значений функции

1. Наибольшее и наименьшее значения функции на отрезке.

Теоретические основы - теорема Вейерштрасса: непрерывная на отрезке [ a, b ] функция f принимает на этом отрезке наибольшее и наименьшее значения.

1.1. Функция монотонна на отрезке [ a, b ].

Если функция возрастает на отрезке [ a, b ], то своё наибольшее значение она принимает на правом конце отрезка, а наименьшее – на левом.

(запись у Мордковича).

Если функция убывает на отрезке [ a, b ], то своё наибольшее значение она принимает на левом конце отрезка, а наименьшее – на левом.

Следует подчеркнуть существенность непрерывности функции на отрезке.

Приведём контрпример: нарушено условие непрерывности функции на отрезке [ a, b ]

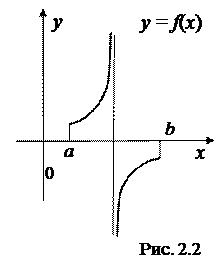
1.2. Функция не монотонна на отрезке [ a, b ].

В этом случае она принимает своё наибольшее или наименьшее значения либо в точках экстремума, либо на концах отрезка [ a, b ].

Алгоритмнахождении наибольшего и наименьшего значений функции

на отрезке [ a, b ].

1. Найти стационарные и критические точки функции.

2. Отобрать из них точки, принадлежащие отрезку[ a, b ].

3. Вычислить значения функции в этих точках.

4. Вычислить значения функции на концах отрезка [ a, b ].

5. Выбрать из значений, полученных в п. 3 и 4 наибольшее и наименьшее.

6. Записать ответ.

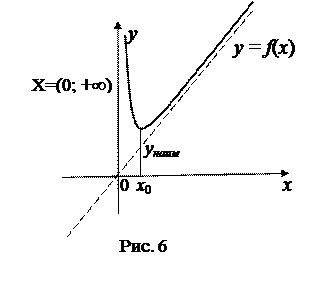
2. Наибольшее и наименьшее значения функции на промежутке.

Теорема. Если функция у = f (x) непрерывна на промежутке Х (отрезке, интервале, луче...) и имеет внутри него единственную стационарную или критическую точку , то

а) если - точка максимума, то в этой точке функция принимает наибольшее значение на промежутке Х;

б) если - точка минимума, то в этой точке функция принимает наименьшее значение на промежутке Х;

Примеры.

№ 1. Правило 1.

Найдите наименьшее значение функции 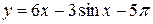на отрезке . Ответ: у_наим.=у(5p/6)= 3/2.

№ 2. Правило 2.

Найдите наибольшее и наименьшее значения функции на отрезке .

- стационарные точки.

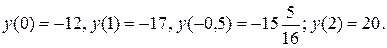
Ответ: у_наиб.=у(2)= 20. у_наим..=у(1)= -17.

№ 3. Правило 3.

Найдите наибольшее значение функции 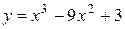на отрезке .

Ответ: у_наиб.=у(0)= 3.

№ 4. Правило 3.

Найдите наибольшее значение функции у = 2 х ² - 13 х + 9 ln x + 8 на отрезке .

. 1 – cтационарная точка.

Производная меняет знак с «+» на «-» – точка максимума.

Ответ: у_наиб.=у(1)= -3.