Алгоритм решения оптимизационных задач

I. Построение математической модели задачи.

1. Выбор оптимизируемой величины.

2. Выбор одной из формул её вычисления.

3. Введение переменной величины х и представление оптимизируемой величины как функции от х.

4. Установление ограничений на х.

5. Составление математической модели задачи.

II. Внутримодельное решение задачи.

III. Интерпретация полученного решения.

Реализуем этот алгоритм на примере приведённой задачи.

I. Строим математическую модель задачи.

1. Площадь.

2. S = ab.

3. Пусть х – одна из сторон прямоугольника, тогда его другая сторона 100 – х.

.

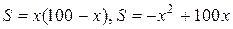4. .

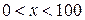5. Найти наибольшее значение функции S (x), если .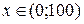

II.

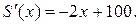
- стационарная точка, причём точка максимума.

S _наиб. = S (50).

III. Размеры участка наибольшей площади с длиной ограды 200 м 50 м ´ 50 м (квадрат).

Ответ: 50 м ´ 50 м.

Чертежи к лекции

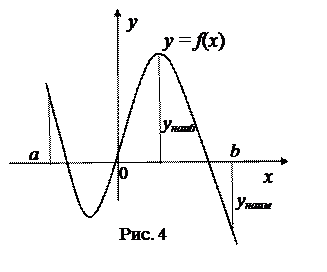
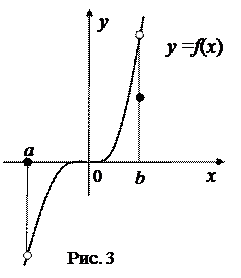
Чертежи к лекции