
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Следование, эквивалентность и преобразование формул
|
|
Введем на множестве M отношения следования и эквивалентности.
Формула B следует из формулы A (обозначается A  B), если она истинна на всех наборах высказывательных переменных, на которых истинна формула A.
B), если она истинна на всех наборах высказывательных переменных, на которых истинна формула A.
Теорема 2.1. Формула B следует из формулы A тогда и только тогда, когда тождественно истинна формула A  B.
B.
Доказательство. Пусть формула B следует из формулы A. Импликация A  B ложна только на тех интерпретациях, на которых формула А истинна, а В ложна, что невозможно в силу условия.
B ложна только на тех интерпретациях, на которых формула А истинна, а В ложна, что невозможно в силу условия.
Покажем обратное. Пусть A  B – тождественно истинна, тогда если на некоторой интерпретации формула А истинна, то и формула В истинна на ней, что и означает A
B – тождественно истинна, тогда если на некоторой интерпретации формула А истинна, то и формула В истинна на ней, что и означает A  B.
B.
Формула A эквивалентна формуле B (обозначается A º B), если они следуют друг из друга, то есть A  B и B
B и B  A. Легко показать, что это определение эквивалентно определению, введенному в п.1.
A. Легко показать, что это определение эквивалентно определению, введенному в п.1.
Теорема 2.2. Формула A эквивалентна формуле B тогда и только тогда, когда тождественно истинна формула A ~ B.
Доказательство аналогично доказательству теоремы 2.1.
Приведем список основных тавтологий, выражающих свойства логических операций.
1. Коммутативность:
X Ù Y º Y Ù X, X Ú Y º YÚ X.
2. Ассоциативность:
(X Ù Y)Ù Z º X Ù (YÙ Z), (XÚ Y)Ú Z º XÚ (YÚ Z).
3. Идемпотентность:
XÙ X º X, XÚ X º X.
4. Законы поглощения:
XÚ (X  Y) º X, X
Y) º X, X  (XÚ Y) º X.
(XÚ Y) º X.
5. Взаимная дистрибутивность конъюнкции и дизъюнкции:
X Ù (YÚ Z) º (X Ù Y)Ú (X Ù Z), XÚ (YÙ Z) º (XÚ Y)Ù (XÚ Z).
6. Свойства констант:
XÙ 0 º Л, XÙ 1 º X,
XÚ 0 º X, XÚ 1 º 1.
7. Законы де Моргана:
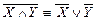 ,
,  .
.
8. Инволютивность:
 .
.
9. Закон противоречия:
 º 0.
º 0.
10. Закон исключенного третьего:
 º 1.
º 1.
Эквивалентность большинства из этих формул непосредственно следует из определения операций или проверяется построением таблиц истинности.
Пусть U – некоторая формула, в которую входит переменная X или подформула А, что обозначается U (¼, X, ¼) или U (¼, А, ¼). Пусть В – некоторая формула. Запись U (¼, X, ¼){ В // X } обозначает формулу, полученную из формулы U подстановкой формулы В вместо всех вхождений переменной X, а U (¼, А, ¼){ В / А } – формулу, полученную из формулы U подстановкой формулы В вместо некоторых (в частности, вместо одного) вхождений подформулы А.
Теорема 2.3 (правило подстановки). Если U (¼, X, ¼) – тавтология и В – любая формула, то U (¼, X, ¼){ В // X } – тавтология.
Теорема 2.4 (правило замены). Если A есть некоторая подформула формулы U и A эквивалентна формуле B, то формула, полученная заменой A в формуле U на B, эквивалентна U. Иными словами, если U (¼, А, ¼) и A º B, то U º V = U (¼, А, ¼){ В / А }.
Например, так как A®B º  , то (A®B)Ù C º (
, то (A®B)Ù C º ( )Ù C.
)Ù C.
Следствие. Если U~A и V~B, то:
1) U  V º A
V º A  B;
B;
2) U 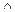 V º A
V º A 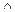 B;
B;
3) U  V º A
V º A  B;
B;
4) (U ~ V) º (A ~ B);
5) 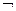 U º
U º  A.
A.
Теоремы 2.3, 2.4 и ее следствие позволяют преобразовывать формулы, упрощая их, и доказывать эквивалентность формул.