
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Булевы функции
|
|
Любую формулу алгебры логики можно рассматривать как функцию, определенную на множестве B = {1, 0}.
Функцией алгебры логики (логической функцией) или булевой функцией f(x1, x2,..., xn) называетсяотображение f: B n® B, определенное на множестве упорядоченных наборов элементов множества B и принимающее значения из этого множества. Обозначим через P n – множество булевых функций n переменных.
Логическую функцию n переменных f(x1, x2,..., xn) можно задать таблицей, в левой части которой перечислены все 2n наборов значений переменных, а в правой части – значения функции на этих наборах.
| x1 x2 ... хn-1 xn | f(x1, x2 ,... хn-1 , xn) |
| 0 0... 0 0 0 0... 0 1 0 0... 1 0 ................ 1 1... 1 0 1 1... 1 1 | f(0, 0,..., 0, 0) f(0, 0,..., 0, 1) f(0, 0,..., 1, 0) ........ f(1, 1,..., 1, 0) f(1, 1,..., 1, 1) |
При любом фиксированном упорядочении наборов булева функция n переменных полностью определяется вектор-столбцом своих значений, размерность которого равна числу наборов значений функции, то есть 2n . Поэтому число различных функций n переменных равно числу различных двоичных векторов длины 2n, то есть  , т.е. |
, т.е. |  | =
| =  .
.
Нулем (единицей) булевой функции назовем упорядоченный набор значений переменных, на котором значение функции равно 0 (1).
Пусть F={  } – некоторое множество булевых функций. Его можно выбрать в качестве основного набора, называемого базисом. Формулой
} – некоторое множество булевых функций. Его можно выбрать в качестве основного набора, называемого базисом. Формулой  над базисом F (обозначается
над базисом F (обозначается  [F]) называется выражение вида
[F]) называется выражение вида  [F]=
[F]=  , где
, где  F, а
F, а  либо переменная, либо формула над F. Таким образом, всякая формула является суперпозицией базисных функций, для её представления обычно применяется форма записи с логическими операциями
либо переменная, либо формула над F. Таким образом, всякая формула является суперпозицией базисных функций, для её представления обычно применяется форма записи с логическими операциями  ~. Каждой формуле однозначно соответствует некоторая булева функция f, в этом случае говорят, что формула
~. Каждой формуле однозначно соответствует некоторая булева функция f, в этом случае говорят, что формула  реализует функцию f (обозначается func F = f). Как будет показано ниже, такая реализация не единственна.
реализует функцию f (обозначается func F = f). Как будет показано ниже, такая реализация не единственна.
Приведем примеры логических функций одной и двух переменных и их реализаций в виде формул.
Логических функций одной переменной четыре: две нуль-местные (j0(х), j3(х)) – константы 0 и 1, значения которых не зависят от значения переменной, и две одноместные функции – тождественная и отрицание.
| x | j0 | j1 | j2 | j3 |
Тождественная функция " повторяет" значение х: j1(х)=х. Функция отрицание возвращает значение, противоположное значению х: j2(х)=х.
Логических функций двух переменных шестнадцать:
| х1 | x2 | j0 | j1 | j2 | j3 | j4 | j5 | j6 | j7 | j8 | j9 | j10 | j11 | j12 | j13 | j14 | j15 |
Рассмотрим подробнее все эти функции.
* j0(х1, х2)  0 и j15 (х1, х2)
0 и j15 (х1, х2)  1.
1.
* j1(х1, х2) = х1 Ù х2 . Эта функция называется ещё логическим умножением и обозначается, также, х1х2.
* j2(х1.х2) = Ø (х1®х2).
* j3(х1, х2) = х1.
* j4(х1.х2) = Ø (х2®х1).
* j5(х1, х2) = х2.
* j6(х1, х2) = 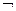 (х1~х2) называются неравнозначностью, разделительной дизъюнкцией или сложением по модулю 2 и обозначается еще как х1Å х2.
(х1~х2) называются неравнозначностью, разделительной дизъюнкцией или сложением по модулю 2 и обозначается еще как х1Å х2.
* j7(х1.х2) = х1Ú х2 .
* j8(х1.х2) =  (х1Ú х2) – антидизъюнкция, которая называется, также, стрелка Пирса и обозначается х1¯ х2.
(х1Ú х2) – антидизъюнкция, которая называется, также, стрелка Пирса и обозначается х1¯ х2.
* j9(х1.х2) = х1~х2. Эту функцию называют еще равнозначностью и обозначают х1º х2 .
* j10(х1.х2) =  .
.
* j11(х1.х2) = х2®х1.
* j12(х1.х2) =  .
.
* j13(х1.х2) = х1®х2.
* j14(х1.х2) =  (х1Ù х2) – антиконъюнкция, которая называется еще штрих Шеффера и обозначается х1 | х2.
(х1Ù х2) – антиконъюнкция, которая называется еще штрих Шеффера и обозначается х1 | х2.
Формулы, реализующие одну и ту же функцию, называются равносильными. Отношение равносильности формул является отношением эквивалентности и обозначается º.
Фиктивной переменной (несущественной) функции f (x 1,..., x n) называется переменная хi, изменение значения которой не меняет значения функции, то есть f (x 1,..., х i-1, 1, x i+1,..., x n) = f (x 1,..., х i-1, 0, x i+1,..., x n).
Например, в функциях j3 и j12 переменная х2 фиктивна, а в функциях j5 и j10 фиктивна переменная х 1.
Функция f (x 1,..., x n), имеющая фиктивную переменную x i, по существу зависит от (n– 1)-й переменной, т.е. представляет собой функцию g (x 1,..., х i-1, x i+1,..., x n). В этом случае говорят, что функция g получена из функции f удалением фиктивной переменной, а функция f получена из функции g введением фиктивной переменной, причём эти функции считаются равными.
Пусть f (x 1, ¼, x n) Î P n – булева функция. Тогда функция f *(x 1, ¼, x n), определенная следующим образом
f *(x 1, ¼, x n) = 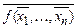 ,
,
называется двойственной к функции f.
Теорема (Принцип двойственности). Пусть F={  }. Тогда, если формула
}. Тогда, если формула  [F] реализует функцию f, то формула
[F] реализует функцию f, то формула  * над базисом F*={
* над базисом F*={  }, полученная из формулы
}, полученная из формулы  заменой функций fi на двойственные им функции fi *, реализуют функцию f *.
заменой функций fi на двойственные им функции fi *, реализуют функцию f *.