
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случайные события. Содержание: Алгебра событий и вероятность
|
|
Содержание: Алгебра событий и вероятность. Вероятность суммы и произведения событий. Условная вероятность. Формула полной вероятности и формула Байеса. Схема Бернулли и ее обобщение. Цепь Маркова. Граф и матрица перехода цепи Маркова.
Случайное событие – событие, которое может произойти и не произойти (попадает стрелка в минешь, лотерея).
Вероятность случайного события – число Р(А), равное отношению числа благоприятствующих ему исходов к общему числу несовместных, равновозможных исходов.
Задача: Монета бросается 3 раза. Найти вероятность того, что выпадет два герба.
Возможные исходы: (Р, Р, Р), (Р, Р, Г), (Р, Г, Р), (Г, Р, Р), (Р, Г, Г), (Г, Р, Г), (Г, Г, Р), (Г, Г, Г) – 8. Р(В)=3/8.
Неразложимые исходы ω 1, ω 2, …, ω n некоторого эксперимента будем называть элементарными событиями, а их совокупность Ω ={ ω 1, ω 2, …, ω n } – пространством элементарными событиями (исходов).
В мат-ке принято выделять оп-и, производимые над определенным числом элементов. А именно, операции, производимые над одним элементом наз. унарными. Над двумя – бинарными, тремя – тернарными. В теории вер-тей мы будем встречаться с двумя бинарными операциями (+ и * событий) и одной унарной операцией (отрицание). Слож-е событий: А+В (или), произ-е А*В (и), отрицание  (не).
(не).
Суммой двух событий наз. событие С=А+В, состоящее в выполнении события А или события В.
Произведением событий А и В наз. Д=А*В, состоящее в совместном исполнении событий А и В.
Противоположным к событию А наз. событие  , состоящее в непоявлении события А, значит дополняющее его до Ω.
, состоящее в непоявлении события А, значит дополняющее его до Ω.
Свойства
1.А+В=В+А 2.А*В=В*А 3.(А+В)*С=АС+ВС
4.двойное отрицание А=А
Вероятность суммы двух событий А и В:
ρ (А+В)= ρ (А)+ ρ (В) - ρ (АВ)
Т.о. если события несовместимые, т.е. АВ≠ 0, то вероятность суммы равна сумме вероятностей: ρ (А+В)= ρ (А)+ ρ (В) (несовместные т.е. одновременно не выполняются АВ≠ 0).
Условной вероятностью ρ (А/В) события А при условии, что произошло событие В (ρ (В)≠ 0), назовем отн-е ρ (А/В)=ρ (АВ)/ρ (В). Это эквивалентно теореме умножения, а именно ρ (АВ)= ρ (В)* ρ (А/В)= ρ (А)* ρ (В/А), т.е. вероятность произведения двух, равна вероятности одного из них, умноженного на условную вероятность другого, при условии, что первое событие наступило.
Два события А и В называются независимыми, если ρ (АВ)= ρ (А)*ρ (В).
Следствия из правил сложения и умножения на вероятностных деревьях:
1. Р(АВ+СD)=P(A)P(B/A)+P(C)P(D/c), где AB и CD- несовместные события.
|

2. Р(А1А2…An-1An)=P(A1)P(A2/A1)…
…P(An/A1A2…An-1).
 Назовем произ-е Р(А1)Р(А2/А1)… Р(Аn/A1A2…An) весом ветви, проходящей через корень дерева и вершины, соответствующей событиям А1, А2, …, Аn. Интерпретацией теоремы сложения и умножения на вероятностных деревьях служит дерево исходов, соответствующее благоприятному событию. Рядом с каждым ребром дерева запишем вероятность исхода, соответствующего конечной вершине этого ребра при условии выполнения произведения всех исходов, соответствующих вершинам пути от корня дерева до данной вершины.
Назовем произ-е Р(А1)Р(А2/А1)… Р(Аn/A1A2…An) весом ветви, проходящей через корень дерева и вершины, соответствующей событиям А1, А2, …, Аn. Интерпретацией теоремы сложения и умножения на вероятностных деревьях служит дерево исходов, соответствующее благоприятному событию. Рядом с каждым ребром дерева запишем вероятность исхода, соответствующего конечной вершине этого ребра при условии выполнения произведения всех исходов, соответствующих вершинам пути от корня дерева до данной вершины.
Пример: Слово «ПАПАХА» разрезано на отдельные буквы. Из этих 6 букв наугад вынимается 4. Какова вероятность получить ПАПА?
А={получить слово ПАПА}. Возьмем в дереве испытаний ветвь, соответствующую событию А и найдем ее вес:
P(A)=2/6*3/5*1/4*2/3=1/30=P(П)*Р(А/П)*Р(П/ПА)*Р(А/ПАП)
Свойства операции сложения и умножения
1. Если АiAj=0 при i≥ 1, j≤ n, то Р(А1+А2+…+Аn)=P(A1)+P(A2)+…+P(An)
2. Если Р(А1А2А3…Аn)=P(A1)P(A2/A1)P(A3/A1A2)… P(An/A1A2…An-1)
Формула полной вероятности
Если событие А может наступить при проявлении одного из нескольких событий (гипотез) Н1, Н2, …, Нк, то для вычисления вероятности события А используют формулу полной вероятности. Для этого необходимо, чтобы гипотезы Hi 1≤ i ≤ k, должны образовывать полную систему событий (гипотез), т.е. должны выполняться два условия:
1. Н1+Н2+…+Нк=W (их сумма должна давать элементарное пространство)
2. HiHj=Æ i≠ j
P(A)=Р(Н1)Р(А/Н1)+Р(Н2)Р(А/Н2)+…+Р(Нк)Р(А/Нк)=  Р(Нi)P(A/Hi) – формула полной вероятности, где Р(Нi) – вероятность гипотезы, P(A/Hi) – условная вероятность события А при выполнении гипотезы Нi.
Р(Нi)P(A/Hi) – формула полной вероятности, где Р(Нi) – вероятность гипотезы, P(A/Hi) – условная вероятность события А при выполнении гипотезы Нi.
Граф формулы полной вероятности

Т.о. вероятность события А равна весу всего графа.
Формула Байеса
Если до опыта вероятности гипотез были Р(Н1), Р(Н2), …, Р(Нn), а в результате опыта появилось событие А, то с учетом этого события «новые», т.е. условные вероятности гипотез вычисляются по формуле Байеса:
Р(Нк/А)=  (к=1, 2, …, n)
(к=1, 2, …, n)
где Р(А)= =  Р(Нi)P(A/Hi)
Р(Нi)P(A/Hi)
Условная вероятность Р(Нк/А) равна отношению веса ветви вероятности графа, проходящего через вершину соответствующую гипотезе Нк, к весу всего графа.
Задача: На заводе изготовляют болты. 1 машина производит 25% изделий, 2 – 35%, 3 – 40%. В их продукции брак составляет 5%, 4%, 2%.
a) Какова вероятность, что случайно выбранный болт – дефектный.
b) Какова вероятность, что он произведен 1, 2, 3 машиной?
a) А={выбрать дефектный болт}.
Выдвигаем гипотезы: Н1 – {болт произведен 1 машиной}, Н2 – {болт произведен 2 машиной}, Н3 – {болт произведен 3 машиной}.
Р(Н1)=0, 25, Р(Н2)=0, 35, Р(Н3)=0, 4; Р(А/Н1)=0, 05, Р(А/Н2)=0, 04, Р(А/Н3)=0, 02.
Р(А)=0, 25*0, 05+0, 35*0, 04+0, 4*0, 02=0, 0345.
b) По формуле Байеса
Р(Н1/А)=(0, 25*0, 05)/0, 0345=29/69.
Р(Н2/А)=(0, 35*0, 04)/0, 0345=28/69; Р(Н3/А)=16/69.
Задача: Предположим, что 5 мужчин из 100, и 25 женщин из 100000 являются дальтониками. Наугад выбираем лицо, страдающее дальтонизмом. Какова вероятность того, что это мужчина?
|

Схема Бернулли и ее обобщения
Схема Бернулли – конечная серия n повтор. независ. испытаний с двумя исходами. Вероятность успеха при одном испытании будем обозначать р. Вероятность неудач q=1-p. Успех – У, неудача – Н. Ограничимся случаем, когда n=3 (3 испытания).
Исходы: Вероятности:
УУУ р3
УУН р2q
УНУ р2q2
НУУ р2q
НУН рq2
ННУ рq2
ННН q3
|

Р3(3)=р3=  Р3(1)=3рq2=
Р3(1)=3рq2= 
Р3(2)=3р2q= 
Р3(0)=q3= 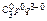
Рn(m)= 
2) Вероятность Рn(m) при данном n сначала увеличивается при увеличении m от 0 до m0, а затем убывает при увеличении m от m0 до n. Т.о. m0 называется наивероятнейшим числом наступления успехов в серии из n повторяемых независимых испытаний.
Нахождение вероятностей по формуле Бернулли для больших n сопряжено с большим числом вычислений.

Часто используют в задачах:
Локальная теорема Муавра-Лапласа
Рn(m)=  ,
,
где φ (х)-табличная функция φ (х)= 
 Интегральная теорема М-Л для вычисления числа успехов в промежутке от m1 до m2.
Интегральная теорема М-Л для вычисления числа успехов в промежутке от m1 до m2.
Рn(m1 £ m£ m2)» 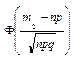 -
-  ,
,
где Ф(х)-табличная функция, равная 
ЗАДАЧА: Вероятность получения с конвейера изделия 1 сорта равна 0, 8. Определить вероятность того, что из взятых проверку 400 изделий 1 сорта будет: а) 320 изделий, б) от 300 до 340 изделий
а) Р400.. Оп(320)= 

б) Р400  .. Оп(300£ m£ 340)=
.. Оп(300£ m£ 340)= 

Теорема Пуассона
 , где l=np
, где l=np
Цепь Маркова
Пусть {Е1, Е2, …, Ек} – множество состояний некоторой системы. В любой момент времени система может находиться в одном из состояний и меняет свое состояние только в моменты t1, t2, …, tn, …Для однородных цепей Маркова вероятность pi, j перехода системы из состояния Еi в Ej за 1 шаг зависит только от того, из какого состояния и в какое осуществляется переход. Вероятности перехода pi, j удобно расположить в виде матрицы
|
