Свойства этой матрицы

1.0£ p_{i, j} £ 1, для любых i, j

2. 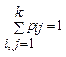, где (i=1, 2, …k) сумма эл-в, стоящ.в строке, д.б.=1.В-р 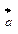=(а₁, а₂, …, а_к), где a_i=P(E_i)- вер-ть нах-ния суммы в сост-и E_i в нач.момент времени(t=0) называется вектором начальных вероятностей.

3.Св-ва однородных Марковских цепей полностью опр-ся в-ром нач.вер-тей и м-цей перехода. В нек.случаях вместо м-цы перехода Р исп-ся ориентир.граф, верши-нами кот.явл.сост-я E_i, а стрелка, идущая от состояния E_i в E_j с числом p_{i, j} показывает, что вероятность перехода из E_i в E_j равна p_{i, j}

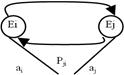
В случае, когда имеется вектор нач.вер-тей, к ориентир.графу, добавляется еще одна вер-на и она соед-ся с вер-ной, соотв-щая сост-ю Е_i ребром, над кот.стоит число а_i.Можно показать, что м-ца перехода Р(n) за n шагов нах-ся как Рⁿ.

Если из Еi в Ej с-ма может прийти с полож.в-ром за конеч.число шагов, то гов-т, что сост-е Ej достижимо из Еi.Сост-е Еi наз. существенным, если для кажд.сост-я Ej, достижимого из Еi.Еi также достижимо из Ej. Иначе Еi несущ-щее состояние.

З-ча: Ч-ца нах-ся на пр-й, движущейся по ней под направл-ем случ.толчков.Ч-ца может нах-ся в точках с целочисл.коорд-ми 1, 2, 3, 4, 5.В точках 1 и 5 нах-ся отражающ. стенки. Если ч-ца нах-ся у стенки, то любой толчок перемещает ее внутрь пром-ка [1, 5] с вер-тью 1.Если ч-ца нах-ся в др.сост-ях, то люб.толчок перемещает ее вправо с вер-тью р, влево с вер-тью q. Найти м-цу перехода и построить соотв-щий ей граф.

Пусть Еi соот-т нах-нию с-мы в точке с целочисл.коор-й i=1, 2, 3, 4, 5.Расположим наши 5 сост-й в вер-нах прав. 5тиугольника.

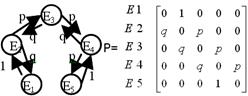
Матрица вероятностей перехода имеет вид

Р= 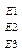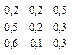Вектор (0, 6; 0, 1; 0, 3). Найти распределение по состояниям р(Е₁) в момент t=2.

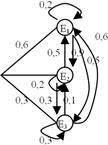
Р(E₁)=0, 6(0, 2*0, 2+0, 3*0, 5+0, 5*0, 6)+0, 1(0, 2*0, 5+0, 3*0, 6+0, 5*0, 2)+0, 3(0, 3*0, 6+0, 6*0, 2+0, 1*0, 5)=0, 437