Задача двох тіл.

Рассмотрим задачу о движении двух взаимодействующих толь­ко между собой материальных точек. Вследствие однородности и изотропности пространства потенциальная энергия взаимодей­ствия может зависеть только от расстояния между точками. Функ­ция Лагранжа для данной задачи запишется в форме

(4.1)

Рассматриваемая система материальных точек замкнута. Поэтому ее импульс сохраняется, и система отсчета центра инерции являет­ся инерциальной системой отсчета. Задачу будем решать в систе­ме отсчета центра инерции. Начало координат поместим в центр инерции, что дает

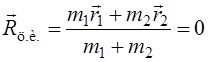(4.2)

Введем радиус-вектор 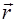, направленный от первой материальной точки ко второй:

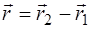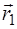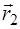(4.3). С помощью формул (4.2) и (4.3) выразим векторы и через вектор 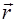: 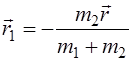; 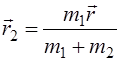(4.4)

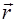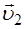Потенциальная энергия теперь зависит только от величины век­тора . Выражая с помощью формул (4.4) скорости и через вектор , кинетическую энергию системы двух материальных точек можно записать как кинетическую энергию одной матери­альной точки массой

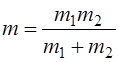(4.5)

Выраженная через радиус-вектор 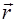функция Лагранжа (4.1) запи­шется в форме

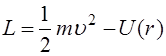(4.6)

Функция Лагранжа (4.6) — это функция Лагранжа одной мате­риальной точки массы 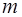, движущейся в потенциальном поле, за­висящем только от расстояния до начала координат. Такое потен­циальное поле называется Центральным полем. Сила, действую­щая в центральном поле на материальную точку, направлена по прямой, соединяющей материальную точку с центром поля:

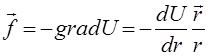(4.7)

Масса 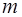, определенная согласно (4.5), называется Приведенной массой. Следовательно, решение задачи двух тел эквивалентно решению задачи о движении в центральном поле материальной точки с массой, равной приведенной массе. После решения задачи о движении материальной точки в центральном поле, координаты двух тел можно получить при помощи формул (4.4).