Бесконечно большие функции

Функция f (x) называется бесконечно большой функцией в точке х = x ₀ (или x → x ₀), если для любого как угодно большого положительного числа K > 0 существует δ = δ (K) > 0, такое, что для всех х, удовлетворяющих условию 0 < | x – х ₀ | < δ, выполняется неравенство | f (x) | > К.
В этом случае пишут

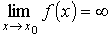
и говорят, что функция стремится к бесконечности при х → х ₀, или что она имеет бесконечный предел в точке х = х ₀. Если же в определении выполняется неравенство f (x) > K (f (x) < – K), то пишут

или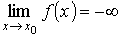

и говорят, что функция имеет в точке х ₀ бесконечный предел, равный + ∞ (– ∞).
По аналогии с конечными односторонними пределами определяются и бесконечные односторонние пределы:

, , , .

Так, например, пишут если для любого как угодно большого положительного числа K > 0 существует δ = δ (K) > 0, такое, что для всех х, удовлетворяющих условию х ₀ < x < х ₀ + δ, выполняется неравенство f (x) > К. Или в символической записи

( K > 0) ( δ = δ (K)> 0)( x₀ < х < x₀+δ): f (x) > K.

Предлагается самостоятельно сформулировать определение бесконечно большой функции при x → + ∞, x → – ∞.