Постановка задачи. Теория механических колебаний имеет многочисленные и весьма разнообразные приложения едва ли не во всех областях техники

Теория механических колебаний имеет многочисленные и весьма разнообразные приложения едва ли не во всех областях техники. Независимо от конструктивного облика различных механических систем их колебания подчиняются одним и тем же физическим закономерностям, изучение которых и составляет предмет общей теории.

Наиболее полно разработана линейная теория колебаний. Еще в XVIII веке в «Аналитической механике» Лагранжа она была развита для систем с несколькими степенями свободы. В работах ряда авторов XIX века (особенно Рэлея) были заложены основы линейной теории колебаний систем с бесконечным числом степеней свободы (т.е. с непрерывным распределением массы по всему объему деформируемой системы). В XXв линейная теория, можно сказать, была завершена; ныне сложность исследований колебательных процессов в линейных системах связана лишь с правильностью оценки существенных степеней свободы и определением внешних воздействий, т.е. с выбором расчетной схемы.

На железнодорожном транспорте гашение энергии необходимо производить как в вертикальном, горизонтальном поперечном, так и в горизонтальном продольном по отношению к движению направлениях. Амортизаторы в первых двух направлениях обычно используются масляные и устанавливаются под углом 45 градусов между вертикальной и горизонтальной поперечной движению плоскостями. Т.е. один амотризатор гасит энергии в двух направлениях. Продольные амортизаторы железнодорожного подвижного состава называют - поглощающий аппарат автосцепного устройства. Поглощающие аппараты различают грузового типа и пассажирского. Поглощающие аппараты грузового типа различают по классам Т0, Т1, Т2, Т3 - в зависимости от энергии, которую он поглощает (50 кДж - первый и 190 кДж - последний) и других его технических характеристик, описанных в ОСТ-32-175-2001.

Равночастотный амортизатор.

При работе двигателей самолетов возникают заметные вибрации всей самолетной конструкции, которые не только вызывают хорошо известный авиационным пассажирам шум, но и оказывают вредное влияние главным образом на самолетное оборудование.
Чувствительные приборы из-за вибрации изнашиваются, теряют точность и постепенно становятся негодными для эксплуатации. Кроме того, по той же причине нарушается нормальная работа оборудования (колебания указательных стрелок, помехи в радиосвязи…)

Одним из средств борьбы с этими явлениями служит амортизация оборудования, т.е. настолько мягкая его подвеска, при которой высокочастотная вибрация практически не передается на амортизированные объекты. Для успеха этой меры стремятся к тому, чтобы отношение частоты возмущающей вибрации к собственной частоте колебаний было возможно большим. Кроме того, желательно, чтобы это отношение было одинаковым для всех разнообразных объектов амортизации, т.е. чтобы одинаковыми были собственные частоты р. Но собственная частота р системы с одной степенью свободы зависит от массы тела m и жесткости упругой связи c:

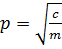
И, следовательно, для разных значений масс m потребуются и различные значения жесткости c. Может оказаться, что для каждого значения массы объекта нужен свой собственный особый амортизатор.

В действительности это не так. Почти 20 лет назад Ю.И.Иориш предложил и разработал идею «равночастотных амортизаторов, т.е. таких упругих элементов, жесткость которых меняется в зависимости от веса амортизируемого объекта P . Равночастотный амортизатор с равным успехом выполняет свою роль независимо от веса подвешиваемого груза (в достаточно широких пределах). Это упрощает стандартизацию и позволяет резко сократить номенклатуру выпускаемых типов амортизаторов. С помощью равночастотных амортизаторов можно добиться неизменности собственной частоты колебаний железнодорожного вагона или автомобиля при любых возможных нагрузках в кухове, а также одинаковых собственных частот станков, устанавливаемых на упругих опорах.

Для выяснения идеи равночастотной амортизации предположим, что связь нагрузки на пружину Р с вызываемой при этом осадкой у нелинейна, Кривая Р=Р(у) является статической характеристикой упругой связи.

Р

А

0 у

Точка А на кривой соответствует нагружению пружины весом mg связанного с ней груза. Подобными характеристиками обладают, например, многие нецилиндрические пружины.

При колебаниях груза около статического уровня сила упругости пружины будет следовать кривой Р(у); однако, если эти колебания достаточно малы, то участок кривой, расположенный вблизи точки А, можно заменить касательной.С помощью такой замены мы получаем линейную колебательную систему, жесткость которой определяется выражением:

А частота – формулой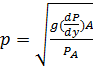

Эта формула показывает, что постоянства частоты Р (т.е. ее независимости от нагрузки Р) можно достигнуть при условии постоянства отношения .

Путь Р- выбранное фиксированное значение собственной частоты. Тогда получаем следующее дифференциальное уравнение для характеристики Р=Р(у):

В котором 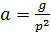– известная постоянная величина. Решение уравнения имеет вид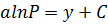

Отсюда непосредственно видно, что интегральные кривые уравнения одинаковы по форме и параллельны друг другу. любая из этих кривых удовлетворяет уравнению, но для определенности решения нужно определить постоянную С и тем самым зафиксировать одну конкретную интегральную кривую - искомую статическую характеристику амортизатора. На первый взгляд для этой цели может быть использовано начальное условие: у=0 при Р=0, так как статичекая характеристика должна проходить через начало координат, но ни одна из кривых через него не проходит. Ю.И.Иориш предложил следующий выход: Пусть Ро- наименьший вес амортизируемого груза, определяемый техническими требованиями. В таком случае амортизатор при Р< Ро может иметь характеристику, не удовлетворяющую основному уравнению, в частности линейную характеристику . Далее будем стремиться к плавности перехода от линейного участка к нелинейному участку, наш выбор будет подчинен простому геометрическому условию:

При P=Pо

Теперь имеем:

Тогда условие приобретет вид где уо – абсцисса точки, в которой соединяются линейный и нелинейный участки характеристики. В конце концов эта величина определяется заданной частотой Р, как это видно из формулы. Следовательно, чтобы найти постоянную С мы должны воспользоваться условием

Тогда найдем

Причем эта кривая начинается в точке с координатами

От это точки к началу координат проводится прямая, уравнение которой имеет вид: .

Научный и технический прогресс приводит к непрерывному нарождению новых понятий, а вместе с тем - к появлению новых терминов. В наши дни этот процесс настолько стремителен, что за ним, вполне естественно, не могут поспевать составители словарей- толковых и переводных.

Так, в современной литературе на английском языке, посвященной проблемам механических колебаний, все чаще встречаются термины «impedance», «receptance», «admittance», «response». ИХ перевод может вызвать затруднение.

Приведем для примера названия трех статей:

1. «Mechanical impedances for thin plates» (Thomas Dan A., J.Acoust. Soc. America, 1960, №10)

2. «The receptances of uniform and nonuniform rotating shafts» (Gladwell G.M.L., Bishop R.E.D., J. Mech. Engng. Sci, 1959, №1)

3. «Response of rigid frame to a distributed transient load» (De Hart R.C. J. Struct. Div. Proc. Amer. Soc. Civil Engrs, 1956, №ST5)

Нам довелось прочитать следующие переводы этих названий:

1а. «Механические импедансы для тонких пластинок»

2а. «Рецептанца вращающихся валов постоянного и переменного сечения».

3а. «Реакция жесткой рамы на распределенную ударную нагрузку».

В первых двух случаях переводчики пошли по пути наименьшего сопротивления и, в сущности, оставили термины без перевода, так как в русской литературе по механике термин «impedance» еще не узаконен, а термин «receptance» вообще отсутствует. Эти термины существуют в литературе по электротехнике, что, однако, не очень помогает делу. Так как, например, термин «impedance», применяемый в электротехнике, нужно еще суметь перевести с «электротехнического» языка на «механический».

Перевод третьего термина «response»- формально точный, так как в любом словаре действительно одним из вариантов перевода этого слова указывается слово «реакция». Но термин «реакция» имеет в русской терминологии по механике вполне определенный смысл, не совпадающий со смыслом термина «response» в названии упомянутой статьи.

Таким образом, в первых двух случаях перевод вообще не является переводом, а в третьем – перевод может вызвать у читателя ложную ассоциацию. Встретившись с этими терминами в оригинале (1, 2, 3) или в переводе (1а, 2а, 3а), можно оказаться в затруднительном положении.

В настоящей работе разъясняется, с какими понятиями следует связывать указанные термины, а также английский термин «admittance» и термин «антирезонанс», все чаще используемый в нашей литературе.

Для выяснения содержания термина «admittance» обратимся к задаче о вынужденных колебаниях упругой системы с одной степенью свободы, когда возмущающая сила изменяется по закону

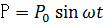(1)

Как известно, соответствующее перемещение равно

(2)

Где m- приведенная масса, c- коэффициент жесткости системы. Вспомним, что под c понимается отношение статически приложенной силы Pст к вызванному ею перемещению yст

(3)

определяющее угол наклона статической характеристики и характеризующее способность системы сопротивляться статическому деформированию.

По аналогии можно ввести понятие «динамической жесткости» как отношения гармониче94ской силы (1) к вызываемому ею динамическому перемещению (2):

(4)

Эта величина зависит не только от параметров системы c и m, но и от частоты ω возмущающей силы. Так, при весьма медленном изменении внешней силы (ω → ∞) динамическая жесткость равна статической жесткости. При определении значении частоты

(5)

Динамическая жесткость обращается в нуль, т.е. система полностью лишается жесткости и возмущающая сила сколь угодно малой амплитуды вызывает неограниченно большое перемещение (резонанс). Понятие динамической жесткости наполнено ясным физическим содержанием и по этой причине широко используется в теории колебаний. Тот же смысл вкладывается иногда и в выражение «механический импеданс». В книге Т. Кармана и М. Био «Математические методы в инженерном деле» указывает также второй вариант значения этого термина: отношение амплитуды силы к амплитуде скорости. Именно в этом значении он ве чаще встречается и в нашей литературе, и для систем с вязким сопротивлением приобретает комплексную форму.

Обратимся теперь к терминам «receptance» и «admittance» и прежде всего подчеркнем, что они полностью равнозначны. Для выяснения их смысла нужно вспомнить, что наряду понятием жесткости (статической или динамической)существует, можно сказать, «взаимное» понятие податливости (также статической или динамической).

Статической податливостью (или – просто податливостью) называют величину, обратную статической жесткости. В строительной механике стержневых систем податливость есть то же самое, что и «единичное перемещение», т.е. перемещение, вызываемое силой, равной единице (в теории упругости аналогом служит функция влияния для перемещений)

Понятие динамической податливости строится подобным же образом. Разделим (2) на (1):

Эта величина определяет амплитуду перемещения, если амплитуда возмущающей силы равно единице. Разумеется, при медленном изменении возмущающей силы, когда ω → 0, динамическая податливость не отличается от статической; если частота ω совпадает со значением (5), то динамическая податливость обращается в бесконечность (резонанс) и т.п.

В современной литературе на английском языке динамическую податливость именуют словом «receptance»

Английскому слову «response» отвечает глагол, означающий по-русски «отвечать», «откликаться», «реагировать».Соответственно слово «response» допустимо переводить как «ответ» и даже «реакция». Однако в последнем случае нужно иметь в виду, что речь идет не о реактивной силе, а о «реагировании» некоторой механической системы на заданные внешние воздействия (обычно имеются в виду динамические нагрузки того или иного рода). В последнее время наибольшее распространение получил термин «отклик», который и следует считать предпочтительным.

Наконец, поясним значение термина «антирезонанс», который нередко применяется в отечественной литературе, посвященной крутильным колебаниям валов.

Прежде всего приведем некоторые элементарные соображения, относящиеся к области статики упругих систем. Допустим, что к упругой системе статически прикладывается сосредоточенная сила. Можно утверждать, что перемещение точки приложения силы по направлению силы не может быть равно нулю. Это вытекает, например, из того что потенциальная энергия деформации, равная работе внешней силы, не может быть равна нулю. Так, невозможно себе представить, чтобы при действии силы, приложенной к упруго закрепленной массе (рис. 1), последняя оставалась бы на месте. Конечно, это также невозможно и в случае более сложной системы, например, изображенной на рис.2

Рис.1

Рис.2

Совершенно по-другому обстоит дело в динамических задачах. Так, например, если сила гармонически изменяется во времени

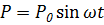(7)

То при некоторых условиях точка приложения силы останется неподвижной; правда, это может быть лишь, если система имеет, по крайней мере, две степени свободы. Это удивительное явление представляет не только очевидный теоретический интерес, но имеет и немалое практическое значение.

Рассмотрим вынужденные колебания четырехмассовой системы, изображенной на рис.2. Если обозначить массы через , а через - жесткости пружин, то уравнения движения можно записать в виде:

Где , – перемещения масс, являющиеся искомыми функциями времени.

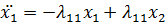
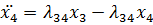
Эта система удовлетворяется решением:

Что означает, что колебания происходят с частотой ω возмущающей силы. Разумеется, что это решение является частным, но оно описывает наиболее важную, стационарную часть процесса; другая часть решения, описывающая колебания с собственными частотами, быстро исчезает вследствие действия неизбежных сил затухания.

Получаем матрицу:

Ее определитель равен 0.

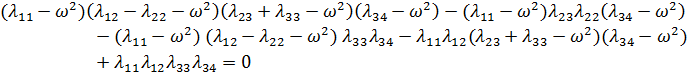
После переобозначения:

Уравнение примет вид:

При

Это уравнение еще надо решить

Упростим задачу и предположим, что тепловоз, масса которого сравним с массой всех вагонов. Будем считать, что состоит из двух элементов.

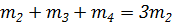
Тогда уравнение примет вид

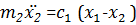
Так же решаем

переобозначим

- )

- )

Составим матрицу из коэффициентов

ее определитель также равен 0.

Вычислим его:

После переобозначения получаем:

Решением этого уравнения являются: