Вибір змінних і структура зв’язків.

Нехай з певних економічних міркувань встановлено, що деякий економічний показник х є причиною змінювання іншого показника у. Статистичні дані по кожному з показників інтерпретуються як деякі реалізації випадкових величин X і Y. Як відомо з курсу теорії ймовірностей, математичним сподіванням випадкової величини називається її середнє (арифметичне чи зважене) значення. А залежність середнього значення від іншої випадкової величини зображується за допомогою умовного математичного сподівання.

Кореляційну залежність між ними або залежність в середньому в загальному випадку можна подати у вигляді співвідношення

, (0.1)

де M (Y | x)= f (x) – умовне математичне сподівання.

Функція f{x) називається функцією регресїі Y на X. При цьому X називається незалежною (пояснюючою) змінною (регресором), Y – залежною (пояснюваною) змінною (регресандом). Розглядаючи залежність двох випадкових величин, говорять про парну регресію.

Залежність Y від кількох змінних, що описується функцією

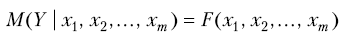(0.2)

називають множинною регресією.

Термін “регресія” (рух назад, повернення до попереднього стану) увів Френсіс Галтон наприкінці XIX ст., проаналізувавши залежність між зростом батьків і зростом дітей. Він помітив, що зріст дітей у дуже високих батьків у середньому менший, ніж середній зріст батьків. У дуже низьких батьків, навпаки, середній зріст дітей вищий. В обох випадках середній зріст дітей прямує (повертається) до середнього зросту людей у даному регіоні. Звідси й вибір терміна, що відбиває таку залежність.

Однак реальні значення залежної змінної не завжди збігаються з її умовним математичним сподіванням, тому аналітична залежність (у вигляді функції y = f(x)) має бути доповнена випадковою складовою u, що, власне, і вказує на стохастичну сутність залежності.

Зв’язки між залежною та незалежною (незалежними) змінними, що описуються співвідношеннями

y = f(x) + u, (0.3)

y = F(x1, x2,..., xm) + u, (0.4)

називають регресійними рівняннями (моделями).

Виникає питання про причини обов’язкової присутності в регресійних моделях випадкового фактора (відхилення). Серед таких причин виокремимо найістотніші.

1. Уведення в модель не всіх пояснюючих змінних. Будь-яка регресійна (зокрема, економетрична) модель – це спрощення реальної ситуації. Остання завжди є складною композицією різних факторів, багато з яких у моделі не враховуються, що призводить до відхилення реальних значень залежної змінної від її модельних значень. Наприклад, попит на товар визначається його ціною, цінами на товари-замінники, на товари, що його доповнюють, прибутком споживачів, їхніми смаками, уподобаннями тощо. Безумовно, перелічити всі пояснюючі змінні практично неможливо. Зокрема, неможливо врахувати такі фактори, як традиції, національні чи релігійні особливості, географічне положення району, погоду та багато інших, вплив яких призводить до деяких відхилень реальних спостережень від модельних. Ці відхилення можуть бути описані як випадкова складова моделі.

У деяких випадках заздалегідь невідомо, які фактори за умов, що склалися, насправді є визначальними, а якими можна знехтувати. Крім того, інколи безпосередньо врахувати якийсь фактор неможливо через відсутність статистичних даних. Наприклад, обсяг заощаджень домогосподарств може визначатися не лише прибутками їх членів, а й станом здоров’я останніх, інформація про яке в цивілізованих країнах становить лікарську таємницю. У деяких ситуаціях ряд факторів має принципово випадковий характер, що додає неоднозначності певним моделям, наприклад погода в моделях, що прогнозують обсяг врожаю.

2. Неправильний вибір функціональної форми моделі. Через слабку вив-ченість досліджуваного процесу або через його мінливість може бути не-правильно підібрано функцію, що його моделює. Це, безумовно, спричинить відхилення моделі від реальності, що позначиться на величині випадкової складової. Наприклад, виробнича функція (Y) одного фактора (X) може моделюватися функцією Y = a + bX, хоча мала б використовуватися інша модель: Y = aX (0 < b < 1), що враховує закон спадної ефективності. Крім того, неправильним може бути добір пояснюючих змінних.

3. Агрегування змінних. У багатьох моделях розглядаються залежності між факторами, що самі є складною комбінацією інших, простіших змінних. Наприклад, при вивченні сукупного попиту аналізується залежність, у якій пояснювана змінна (сукупний попит) є складною композицією індивідуальних попитів, що також може виявитися причиною відхилення реальних значень від модельних.

3. Помилки вимірювань. Якою б якісною не була модель, помилки вимірювання змінних впливатимуть на розбіжності між модельними та емпіричними даними, що також позначиться на величині випадкового члена.

4. Обмеженість статистичних даних. Найчастіше будуються моделі, що описуються неперервними функціями. А для оцінювання параметрів моделі використовується набір даних, що має дискретну структуру Ця невідповідність знаходить відображення у випад­ковому відхиленні.

6. Непередбачуваність людського фактора. Ця причина може “зіпсувати” найякіснішу модель. Дійсно, при правильному виборі форми моделі, скрупульозному доборі пояснюючих змінних неможливо спрогнозувати поведінку кожного індивідуума.

Сукупність методів, за допомогою яких досліджуються та узагальнюються взаємозв’язки кореляційно пов’язаних змінних, називається кореляційно-регресійним аналізом.

Зазначеними методами розв’язують дві основні задачі:

1) знаходження загальної закономірності, що характеризує залежність двох (чи більше) кореляційно пов’язаних змінних, тобто розробка математичної моделі зв’язку (задача регресійного аналізу);

2) визначення тісноти зв’язку (задача кореляційного аналізу).

Здебільшого процедура аналізу зв’язку між змінними дає змогу встановити його природу тобто визначити форму залежності між змінними.

Побудова якісного рівняння регресії, що відповідає емпіричним даним і цілям досліджень, є досить складним процесом. Його можна розділити на три етапи:

1) вибір форми рівняння регресії;

2) визначення параметрів обраного рівняння;

3) аналіз якості рівняння та перевірка адекватності рівняння емпіричним даним, удосконалення рівняння.

Вибір форми зв’язку змінних називається специфікацією моделі регресії.

У випадку парної регресії вибір формули звичайно здійснюється за графічним зображенням реальних статистичних даних у вигляді точок у декартовій системі координат, що називається кореляційним полем (діаграмою розсіювання) (рис.1.1).

Рисунок 1.1 – Кореляційне поле

На рис.1.1 проілюстровано три ситуації. На графіку 1.1, а взаємозв’язок між X і Y близький до лінійного, і пряма 1 досить добре узгоджується з емпіричними точками. Тому щоб описати залежність між X і Y, доцільно вибрати лінійну функцію Y = b0 + b1X.

На графіку 1.1, б реальний взаємозв’язок між X і Y, найімовірніше, описується квадратичною функцією Y = аX² + bX + с (лінія 2).

На графіку 1.1, в явний взаємозв’язок між X і Y відсутній. Тому щоб краще вибрати форму зв’язку необхідно, можливо, збільшити кількість спостережень – точок кореляційного поля або скористатися іншими способами вимірювання показників.

У випадку множинної регресії визначити форми залежності ще складніше.

Якщо природа зв’язку невідома, то співвідношення між показниками описують за допомогою наближених спрощених форм залежностей, насамперед лінійних.

Наприклад, Кейнс запропонував лінійну формулу залежності індивідуального споживання C від доходу Y: C = c0 + bY, де c0 > 0 – величина автономного споживання; b – гранична схильність до споживання, 0 < b < 1.

Однак поки не обчислено кількісні значення коефіцієнтів c0 і b та не перевірено надійність отриманих результатів, зазначена формула залишається лише гіпотезою.